Complementary Angle|Definition & Meaning

Properties and Types of Complementary Angles 

There are different properties of Complementary angles that are following

• If two angles sum is equal to 90 degrees, they are said to be complementary.
• They might be adjacent or not.
• Even though the total of three or more angles is 90 degrees, they cannot be complementary.
• When two angles are complementary, each angle is called the “complement” or “complementary” of the other.
• A right-angled triangle has two complimentary sharp angles.

There are two types of complementary angles i.e. Adjacent Complementary angles and non-adjacent Complementary angles.

Two angles whose sum is 90  and they have a common vertex and arm are known as adjacent complementary angles s shown in figure 3.

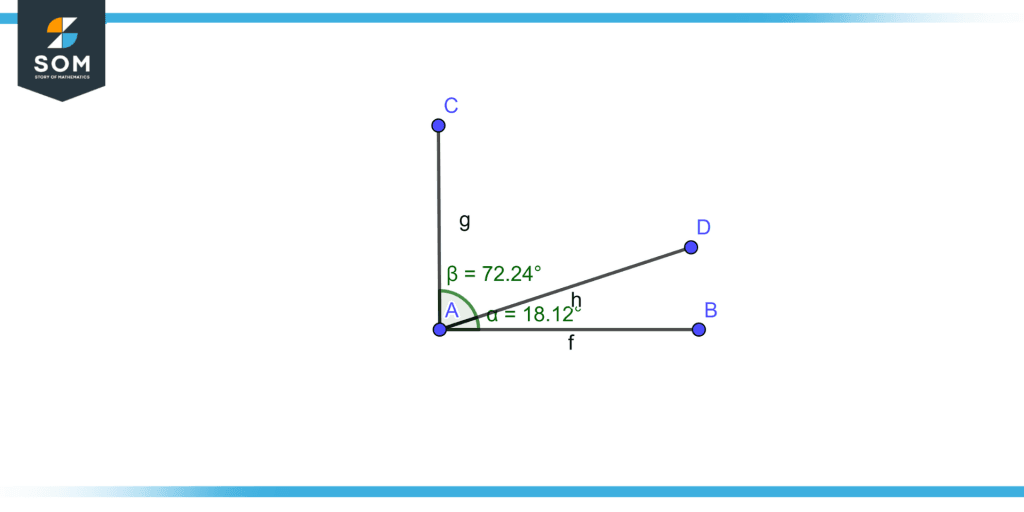
Figure 1 – Adjacent complementary angles

In figure 3 ∠DAB is 18.12°and ∠CAD is 72.24° the sum of  angles is  90° .

If two complementary angles are not adjacent to each other they are non-adjacent complementary angles as illustrated in figure 4.

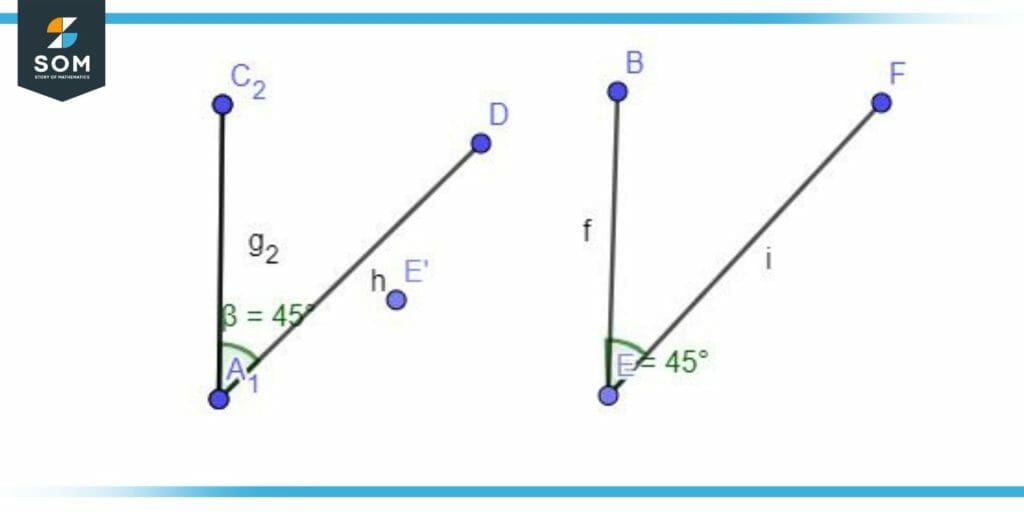
Figure 2 – Non-adjacent complementary angles

In figure 4, both the angles are non-adjacent, and their sum will be equal to 90°.

Complement of an Angle

Each angle is referred to as a “complement” of the other, and we know that the total of two complimentary angles equals 90 degrees. Therefore, an angle’s complement may be calculated by deducting it from 90 degrees. 90-x° is the counterpart of x°. Let’s calculate the angle’s complement, which is 57°. By deducting 57° from 90°, you may find its counterpart, which is 33°: 90° – 57°. Therefore, 33° is the complement of a 57° angle.

Proof of Complementary Angles Theorem

There are pairs of complementary angles that add up to 90°. Consider a diagram illustrated in Figure 2 to prove the complementary angle theorem.

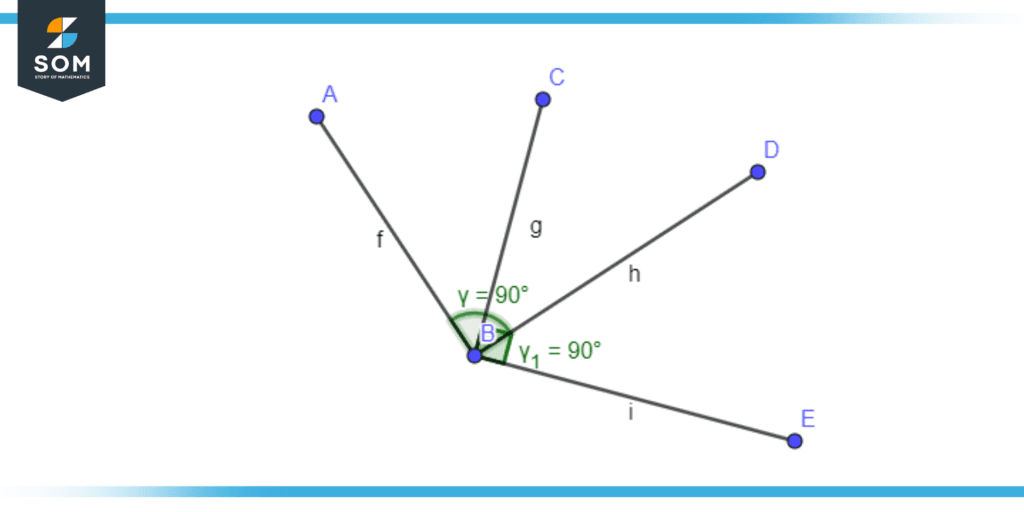
Figure 3 – Complementary angles.

We assume that <CBD is complementary to ∠ABC and ∠DBE.

As per the definition of Complementary angles, ∠CBD +∠ABC=90°, and  ∠CBD +∠DBE=90°. Now we can say that ∠ CBD +∠ABC=∠CBD +∠DBE. Now we can see that ∠ABC =∠ DBE; hence theorem is proved.

Difference Between Supplementary and Complementary Angles

Two angles are called supplementary if their sum is 180° and two angles are complementary of each other if their sum is 90°. The supplement of an angle x° is 180-x° whereas the complement of an angle x° is 90-x°. Both the supplementary angles can be joined to form a straight angle, whereas the complementary angles can be joined to form a right angle.

Complementary Angles And Their Importance in Mathematics

Complementary angles are one of the most important parts of trigonometry. Trigonometry is one of the most significant areas of mathematics that has a wide range of applications. The study of the connection between the sides and angles of the right-angle triangle is essentially the focus of the field of mathematics known as “trigonometry.”

As complementary angles is the angles whose sum is 90, are used in vast fields like astronomical research. Architects, surveyors, astronauts, physicists, engineers, and even crime scene investigators use complementary angles in a variety of professions.

Significance Of Right Angle Triangles

More specifically, right-angled triangles with a 90° internal angle are the subject of trigonometry. We may use trigonometry to determine any missing or unknowable side lengths or angles in a triangle. All lengths in right-angled are not equal to each other. The side with 90° is known as perpendicular, the opposite side of the perpendicular is the hypotenuse, and the line segment on which they stand is the base of the triangle, as shown in figure 1.

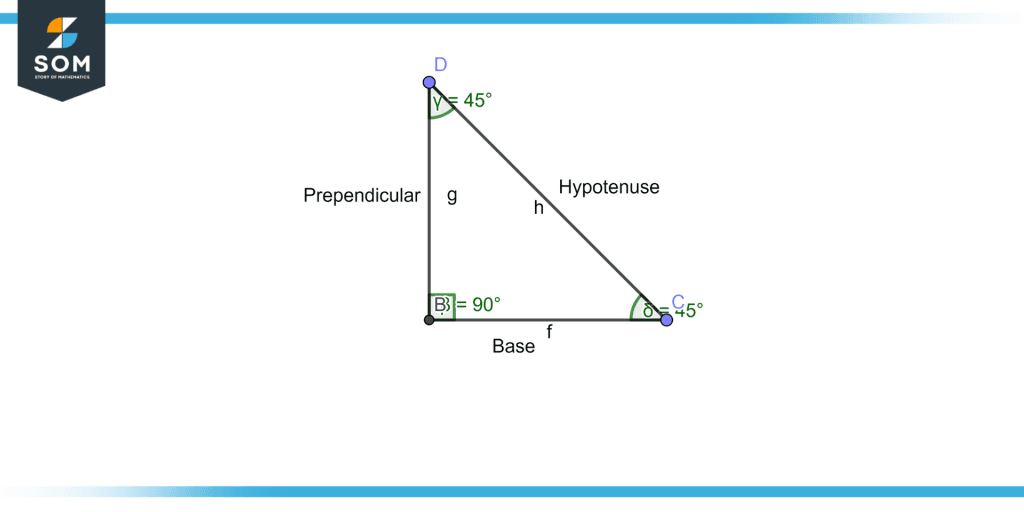
Figure 4 – A right-angled triangle; notice the presence of the ninety-degree angle.

As illustrated in Figure 1 we can see that the angle between the line segment h and f is 45° and between g and h is 45°, and the sum of the two angles is 90°, so both angles are the complement of each other.

The relationship between the acute and right angle of the right-angled triangle is defined by the trigonometric ratios, which are given below

$\sin(\theta)$= $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

$\cos(\theta)$= $\dfrac{\text{Base}}{\text{Hypotenuse}}$

$\tan(\theta)$= $\dfrac{\text{Perpendicular}}{\text{Base}}$

$\csc(\theta)$= $\dfrac{\text{Hypotenuse}}{\text{Perpendicular}}$

$\sec(\theta)$= $\dfrac{\text{Hypotenuse}}{\text{Base}}$

$\cot(\theta)$= $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

Finding Angles Given That They Are Complementary

Example 1

Calculate the values of two complementary angles A and B if A = (2x – 18)° and B = (5x – 52)°.

Solution

∠A = (2x – 18)° and ∠B = (5x – 52)°

We know that,

Sum of two complementary angles = 90°

∠A + ∠B = 90°

(2x – 18)° + (5x – 52)° = 90°

 7x – 70° = 90°

 7x = 90° + 70° = 160°

 x = 160°/7 = 22.85°

Now,

∠A = (2 × (22.857) – 18) = 27.714°

∠B = (5 × (22.857) – 52) = 62.286°

Hence, ∠A = 27.714° and ∠B = 62.286°

Example 2

Find the value of X in given figure 5.

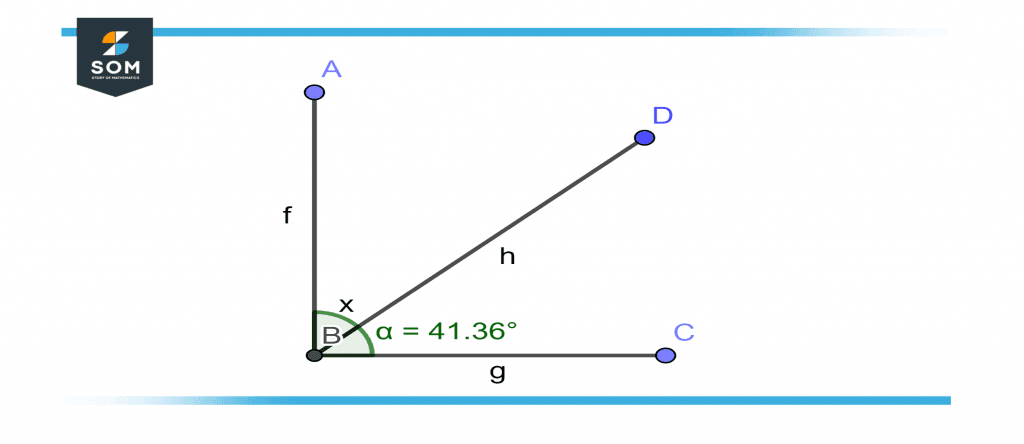
Figure 5 – Finding the unknown complementary angle x.

Solution

As illustrated in figure both angles x and 41.36° are complementary angles so their sum is 90°.

x + 41.36° = 90°

x = 90° – 41.36°

x = 48.64°

Therefore, the value of angle ‘x’ is 48.64°.

Example 3

Find x if the given angles illustrated in figure 6 are complementary angles.

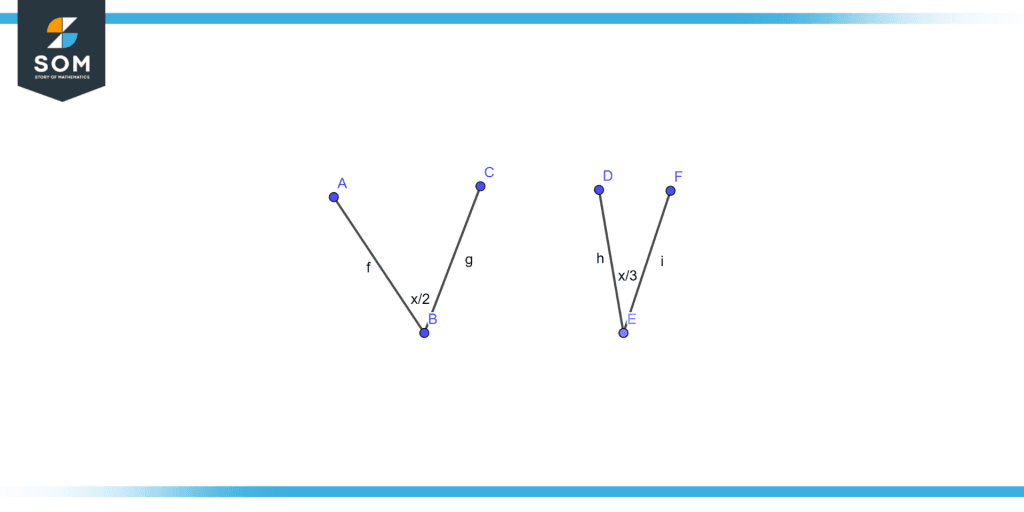
Figure 6 – Non-adjacent complementary angles with unknown values.

Solution

As we know the sum of two complementary angles is 90°

$\dfrac{x}{2}$ + $\dfrac{x}{3}$ = 90°

$\dfrac{5x}{6}$ = 90°

 x = 90° × $\dfrac{6}{5}$ = 108°

Therefore, the value of x is 108°.

Example 4

Find the values of angles A and B such that ∠A = (x – 25)° and ∠B = (2x − 25)° if both A and B are complementary of each other.

Solution

As ∠A and ∠B both are complementary so their sum is 90°.

 ∠A + ∠B = 90°

 (x – 25)° + (2x – 25)° = 90°

 3x – 50° = 90°

3x = 140°

 x = 46.6°

Thus, ∠A = 46.6 – 25 = 21.6° and ∠B = 2 (46.6) – 25 = 68.2°.

Therefore, ∠A and ∠B are 21.6° and 68.2°, respectively.

All images/mathematical drawings were created with GeoGebra.

Complement Set Definition < Glossary Index > Complex Number Definition