JUMP TO TOPIC
Complex Number|Definition & Meaning
Definition
In mathematics, a complex number is a part of a number system and is a sum of real and imaginary number parts of a number system. Every complex number may be written as a + bi, where a is the real part and b is the imaginary part.
Graphing a Complex Number
A complex number’s real and imaginary components, Re(z) and Im(z), can be written as a pair of ordered coordinates on the euclidean plane. The complex plane, sometimes known as the Argand Plane after its discoverer Jean-Robert Argand, is the euclidean plane in the context of complex numbers. The natural component a, concerning the x-axis, and the imaginary component ib, concerning the y-axis, are used to depict the complex number z = a + ib. Let us make an effort to define the two key phrases associated with the argand plane’s representation of complex numbers: the modulus and argument of the complex number.
Modulus of Complex Number
In the Argand plane, a complex number is represented by the coordinates (a, ib), and its distance from the origin is known as its modulus. It is the straight-line distance between the starting point (0, 0i) and the given coordinates (a, ib).
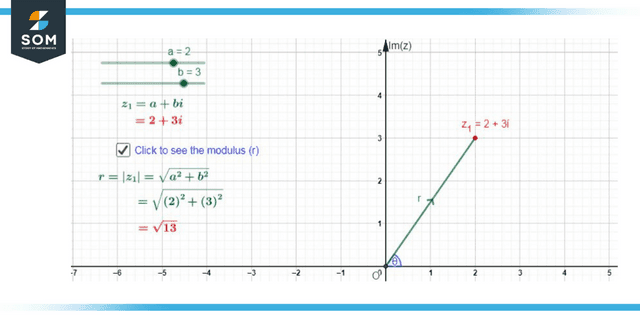
Figure 1: The modulus of a complex number.
Furthermore, this can be interpreted as a derivation of the Pythagorean theorem, with the modulus standing in for the hypotenuse, the fundamental component for the base, and the imaginary portion for the apex of the right triangle. In other words, the real part is squared along with the complex part, and the entire bracket is square-rooted. The answer to the problem gives the distance from the origin, or the modulus.
The Argument of a Complex Number
Complex numbers have arguments that describe the anticlockwise angle formed by the line between the complex number’s geometric representation of the origin and the positive x-axis. We calculate it by dividing the imaginary component by the real component of the complex number.
Cartesian Complex Plane
The usage of Cartesian coordinates on the complex plane is implicit in the definition of complex numbers, which requires using two arbitrary absolute values. The real part is typically displayed with rising values to the right along the horizontal (real) axis, often just called the x-axis. In contrast, the imaginary part is typically displayed along the vertical (imaginary) axis or the y-axis, with increasing values to the top.
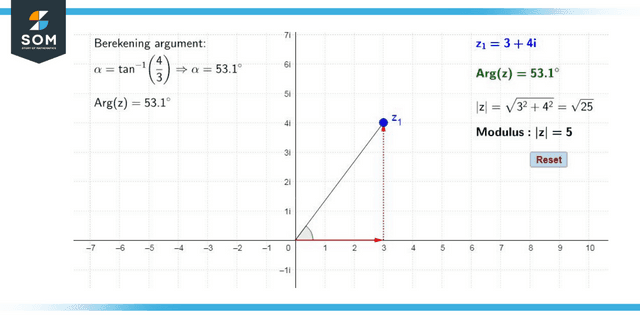
Figure 2: The argument of a complex number.
Coordinated point or position vector from the origin to the numbered location on the chart. A complex number z can have Cartesian, rectangular, or algebraic representations for its coordinate values.
In this context, multiplying a complex number by $i$ is the same as turning the position vector 90 degrees to the left of the x-axis.
Properties of a Complex Number
The following complex number properties will aid in your understanding of complex numbers and your ability to do arithmetic on them.
Conjugate of a Complex Number
The conjugate of a complex number is simply the original number with the imaginary component replaced by its additive inverse. The real component remains the same in the conjugate.
Two complex numbers are conjugates of each other if both their sum and product give a real number. Often, we use the conjugate by multiplying and dividing it with the provided equation to reduce the problem into a simpler sum.
Reciprocal of a Complex Number
If z = a + bi is a complex number, the reciprocal is (1 / z) = 1 / (a + bi). Evidently, multiplying a complex number by its reciprocal gives the complex unity 1 + 1i. When dividing by another complex number, the reciprocal is a helpful tool.
Ordering of a Complex Number
Ordering is not possible with complex numbers, even though it is possible in real numbers and related number systems. It is not possible to rank a complex number since they lack the organization of a field, and they cannot be sorted in any way that allows for addition or multiplication. A complex number’s magnitude, or how far it is from zero (the modulus), can be used to express it in a two-dimensional Argand plane.
Operations on Complex Numbers
Complex numbers are amenable to the same arithmetic operations as their natural-number counterparts, including addition, subtraction, multiplication, and division. The different arithmetic operations performed on complex numbers are described here. The addition and conjugate concept of the complex number is explained in the examples at the end.
Addition of Complex Numbers
Adding a natural number to a complex number requires adding the natural number to the real part of the complex number.
We add complex numbers the same way as we add natural numbers, though with a small difference. Since complex numbers contain real and imaginary parts, we need to ensure we add compatible parts separately (i.e., real + real and imaginary + imaginary). Thus, if x = a + bi, and y = c + di, then z = x + y = (a + c) + (b + d)i.
Clearly, if the second complex number is purely real or purely imaginary, only the real or imaginary part is summed in the result.
There are 5 laws for the additive property of a complex number:
- Closure Law
- Commutative Law
- Associative Law
- Additive Identity
- Additive Inverse
Figure 3: Addition of two complex numbers.
Subtraction of Complex Numbers
The method of subtracting complex numbers from natural numbers is like the process of subtracting natural numbers, again keeping the compatibility of real and imaginary parts in mind. In this case, subtracting any two complex numbers involves performing the operation across the real part of each number and then repeating the procedure across the imaginary part of each number.
Things To Remember
These two points should be kept in mind while solving a problem with complex numbers:
- Real numbers are essentially complex numbers with purely real parts. However, every complex number is not necessarily real, as it can be purely imaginary or a mixture of real and imaginary.
- The distinction between complex numbers and imaginary numbers is that complex numbers can exist without becoming imaginary numbers.
Solved Examples of Complex Number Exercises
Example 1
What is the final solution after multiplying (2 + 3i) (2 – 6i)?
Solution
It should be noted that the real number of the problem is added or multiplied with the real part only; whereas, the imaginary number is added or multiplied with the complex region only. Therefore, the solution is as follow:
= 4 – 12i + 6i – 18i^2
= 4 – 6i + 18
= 22 – 6i
If plotted, “22” will be on the real axis or the x-axis, and the “-6” will be on the imaginary axis or the y-axis.
Example 2
Simplify the following expression using the complex conjugate:
(7 – i)/(2 + 10i)
Solution
Here the denominator’s conjugate is multiplied and divided by the problem given above.
= [(7 – i)/(2 + 10i)] x [(2 – 10i)/(2 – 10i)]
= (14 – 72i + 10i²)/(4 – 100i²)
= (4 – 72i)/104
= (4/104) – (72/104)i
Simplified Version:
= (1/26) – (9/13)i
All images/mathematical drawings were created with GeoGebra.
