JUMP TO TOPIC
Component Vector|Definition & Meaning
Definition
Any vector can be broken down into its constituent parts pointing in a set of well-defined directions. These parts are called the vector’s components.
It is sometimes necessary to decompose the vector into its parts to help perform various vector operations.
A vector’s components dictate how much of the vector’s magnitude lies along each of the axes of the coordinate system.
What Is a Component Vector
A vector can be split down into its components to reveal its structure. Vectors can be computed by first dividing the components of a vector for each of the axes, and then we may compute the components. In general, vectors are represented in either a two-dimensional complex plane with an x-axis and a y-axis or a three-dimensional space with an x-axis, y-axis and z-axis correspondingly.
Vectors are a special kind of mathematical representation that has both magnitude and direction associated with them.
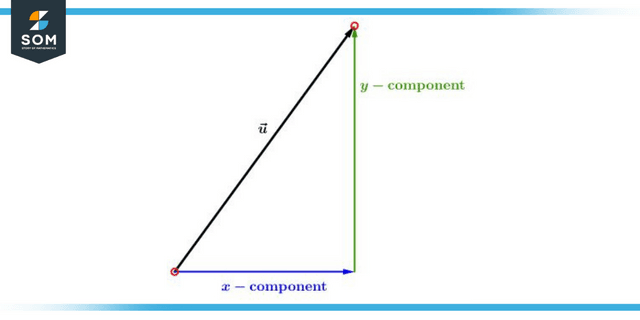
Figure 1: Components of a vector
In a coordinate system with only two dimensions, the direction of a vector can be found by an angle the vector makes with the positive x-axis.
The Formula of Component Vector
We want to define a vector V in a plane with only two dimensions. The vector V can be split into two components: denoted by Vx and Vy.
Now let us assume that a right angle, denoted by the symbol, is established between the component x of the vector V. If we draw a parallel line to the y-component. The vector V and its x-component, denoted by Vx, will create a triangle with a right angle (Vy).
We now have the expression:
cos θ = Vx / V
sin θ = Vy / V
As a result, the following formula can be used to find the constituents of any given vector:
Vx = V cos θ
Vy = V sin θ
The magnitude of the vector, which is termed V, may be determined with the help of the Pythagorean theorem.
In addition, the vectors can also be expressed in the three-dimensional space using the equation A=ai+bj+ck. The unit vector all along the x-axis, y-axis, and z-axis are denoted by me, j, and k, respectively, in this expression. These unit vectors help distinguish the constituents of the vectors about each of the axes, and they do so by providing a reference point.
The components of vector A about the x-axis, y-axis, and z-axis are denoted by the letters a, b, and c.
Orthogonal Vectors
Using the coordinate system to represent three-dimensional vectors is a simple process. Let’s acquire a basic understanding of orthogonal representation under our belts before moving on to the topic of vector representation.
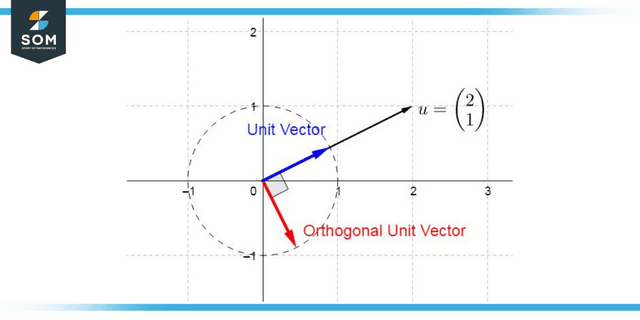
Figure 2: Representation of orthogonal vectors
When we talk about orthogonal representation in the context of coordinate geometry, we refer to parameters that are placed at right angles. In an orthogonal three-dimensional system, we have three axes that are perpendicular to each other. These axes represent the x, y, and z dimensions, respectively.
We can have three distinct unit vectors when dealing with orthonormal or orthogonal systems, with one unit vector corresponding to each direction.
Are Scalars Comprised of Components of Vectors?
Scalars are not the same thing as the components of a vector. The individual components that make up a vector are likewise vectors, and like the vector as a whole, they have both a magnitude and a direction. It is also possible to specify the components of a vector for one of the axes in either the coordinate plane or the three-dimensional space.
Properties of Vector Component
- Magnitude and direction are the two sub-components that can be extracted from a vector when broken down.
- We may compute the vector’s horizontal and vertical components using a hypotenuse method. This approach requires us to use the angle that the vector creates with the two components as the input.
- Scalar quantities are physical quantities that a single number can represent. In contrast, vector quantities are physical quantities that can be represented by two components: direction and magnitude. Scalar quantities include mass, height, volume, and area, while vector quantities include velocity, displacement, and acceleration.
- It is possible to decompose vector values into their parts along the horizontal and vertical axes.
- A unit vector is known as a vector with a magnitude of 1.
- Since vectors are primarily represented by arrows that have both a magnitude and a direction, any quantity represented by a vector must also have both a magnitude and a direction.
- Displacement, acceleration, and velocity are the three most frequent physical quantities typically expressed in vectors. Because acceleration is the rate of velocity change relative to time, it is necessary to consider both the direction and amount of acceleration.
- Because the computation of one requires the value of the other, movement, speed, and acceleration are all related to one another in some way. This is because all three are considered to be vector quantities.
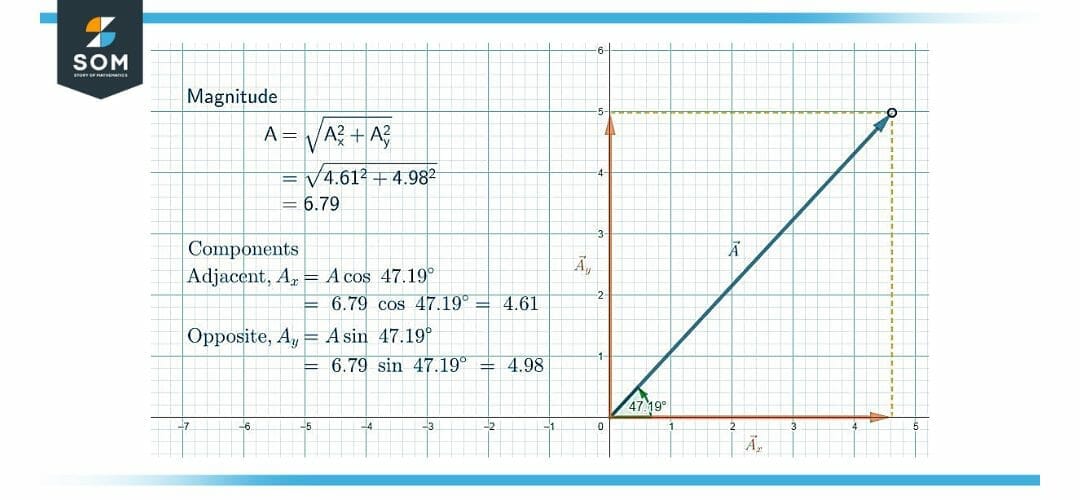
Figure 3: Different aspects of a component vector
Example Problems Requiring Vector Components
Example 1
A boat travels at the velocity of 30 kmph to the west. A current of magnitude 7 kmph is present at N30° W, find the velocity and direction of the boat?
Solution
Vector B = <30 cos(180°), 30 sin(180°)>
Vector C = <7 cos(120°), 7 sin(120°)>
Addition of both the vectors give a resultant vector, <-33.5, 6.06>.
To find the velocity:
Modulus of the resultant = \[\sqrt{(-33.5)^2 + (6.06)^2} \]
= 33.04 kmph.
To find the distance:
Tan θ = 6.06 / -33.5
Tan^-1 (6.06 / -33.5) = θ
= -10.25
Example 2
An outer force is pushing a box on a ramp with 20N towards the west; whereas, the friction applied is 10N to the east because of the conveyer belt. Find the magnitude with which the box will move and the direction of the movement.
Solution
Force applied to the west is greater than the force applied to the east; therefore, the magnitude of the force is 10N.
20N – 10N = 10N force to the west
In the ideal case, friction is neglected, and therefore, the acceleration would be 20N to the west.
All images/graphs are created using GeoGebra.
