JUMP TO TOPIC
Compounding|Definition & Meaning
Definition
Compounding is the process of earning on the initial investment and the interest credited to the principal investment. It has the ability to make investments grow at a larger scale with the passing of time. It can be applied on a loan or on an initial investment/deposit in an account.
Compounding refers to the exponential growth of money as shown in figure 1. The exponential graph shows that after reaching a certain point, the y-values drastically increase which refers to the substantial amount of earnings.
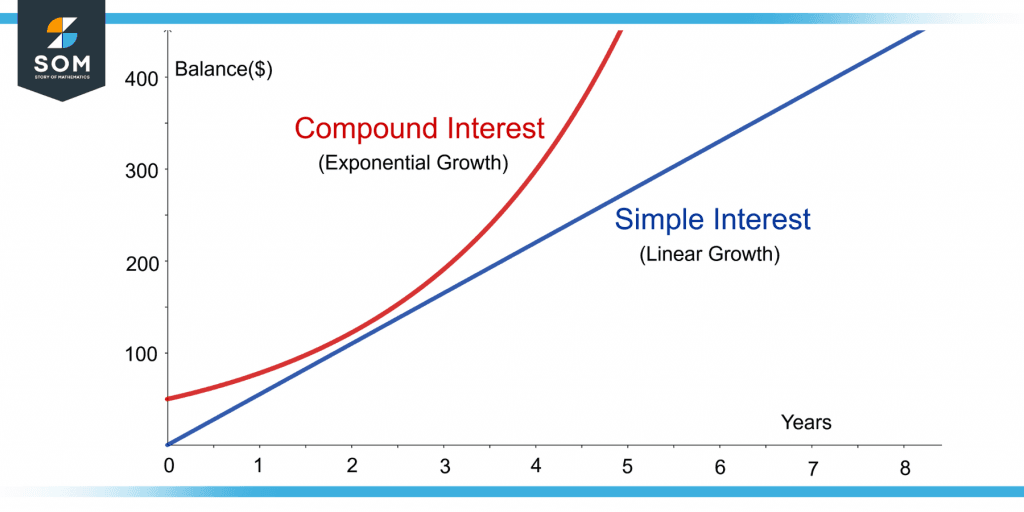
Figure 1 – Exponential Growth of Compounded Interest Compared to the Linear Growth of Simple Interest
Types of Interest
We normally encounter two types of interest: simple and compounded. To understand compounded interest comprehensively, one must know about simple interest.
Simple Interest
Simple interest is the process of applying interest on a loan or a deposit over a period of time.
Unlike compounded interest, simple interest applies only to the principal investment and not the interest accumulated over time.
Figure 2 shows an example of simple interest.
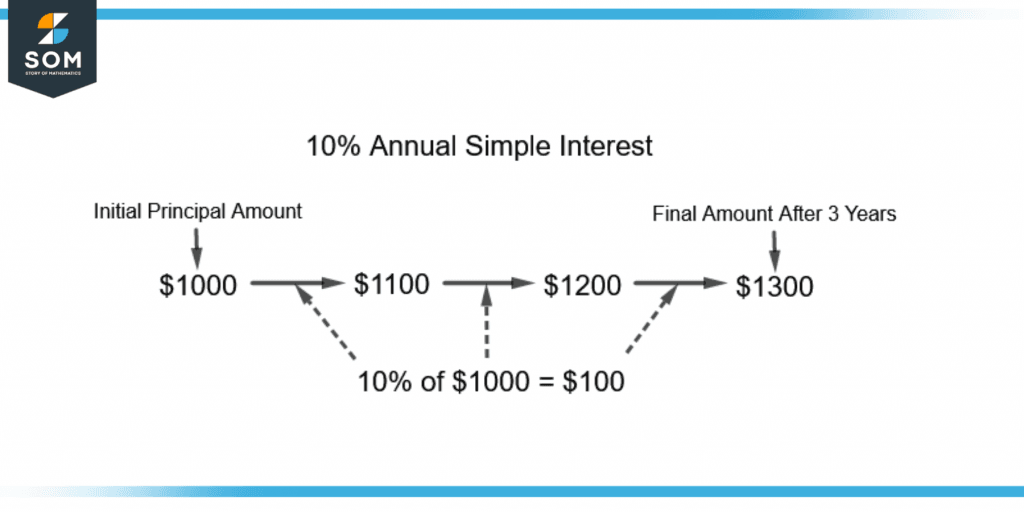
Figure 2 – Demonstration of Simple Interest
The simple interest in figure 2 can be calculated using the formula given below for simple interest.
A = P(1 + rt)
Where P, A, r, and t are respectively the principal investment, the final amount, the annual interest rate, and the time passed since the initial investment (in years).
From figure 2:
P = $1000 , r = 10% = 0.1 , t = 3 years
So, the final amount will be:
A = P(1 + rt)
A = 1000[1 + 0.1(3)]
A = 1000[1 + 0.3]
A = 1000(1.3)
A = $1300
Compounded Interest
Compounded Interest is earning interest on the initial investment and on the previously accumulated interest.
It means that as time goes by, the principal investment becomes the previous principal plus the interest added to it, on which the interest is added again and again.
Figure 3 shows the same example as in figure 2 for compounded interest.
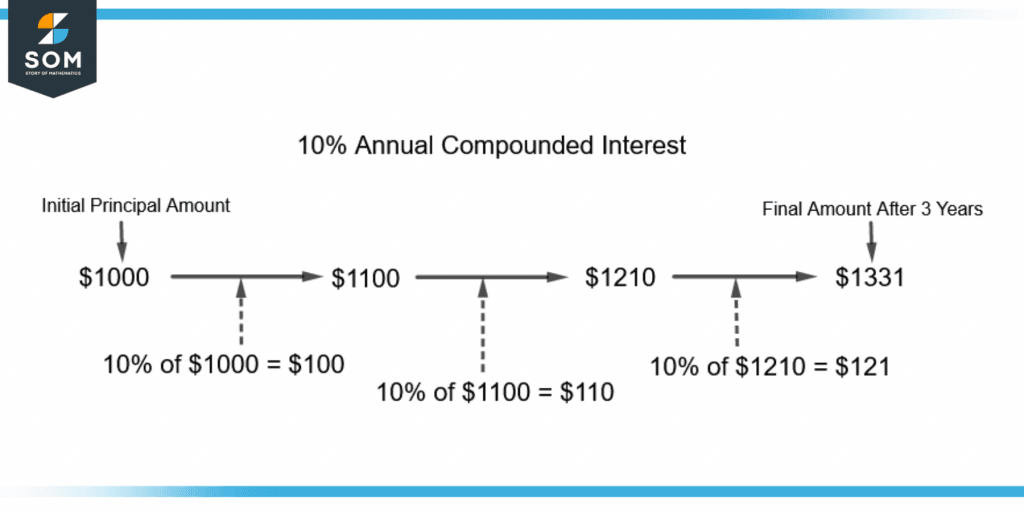
Figure 3 – Demonstration of Compounded Interest
Compared to simple interest, compounded interest yields more earnings over the same time period hence it is more potent in financial dealings.
Periodic Compounded Interest
Periodic Compounding refers to interest compounded over a period of time. The formula for periodic compounded interest is given as follows:
\[ A = P { \Big[ 1 + \frac{R}{n} \Big] }^{nt} \]
Where A and P are the final and principal base amounts, and R, n, and t are respectively the interest rate, the number of times interest is received in a year, and the time elapsed (in years).
The interest rate R is usually given in percentage. It is divided by 100 to get the rate in decimal which is plugged into the equation.
From figure 3, the compounded interest can be calculated as follows:
\[ A = 1000 { \Big[ 1 + \frac{0.1}{1} \Big] }^{1(3)} \]
A = 1000 $[ 1 + 0.1 ]^{3}$
A = 1000 $[ 1.1 ]^{3}$
A = 1000 (1.331)
A = 1000 (1.331)
A = 1331
So, the final earnings amount to $1330.
The Role of Time in Interest Compounding
Time plays an essential role while dealing with interests. For compounded interest, it serves as a key pillar for enhancing the investment to a greater extent.
Figure 4 shows the importance of time in compounded interest.

Figure 4 – Importance of Time In Compounded Interest
With twice the time gone by, the final earnings become approximately twice with compounded interest. Hence more time produces more gains in investment.
Value of “n”
The value of n changes with the compounded time period associated with the annual interest explained as follows:
Monthly
For monthly compounded interest, the value of “n” is 12 as the interest received would be twelve times a year.
If the 24% annual interest rate is compounded monthly, the extra money received every month would be according to 24/12 = 2% interest rate.
Weekly
For compounded interest applied weekly, “n” will be 52 as there are fifty-two weeks in a year.
Daily
The value of “n” will be 365 for daily compounding as there are 365 days in a year.
Quarterly
The number of times interest is received in a year quarterly would be four times, so the value of “n” would be 4.
Semi-Annually
Semi-annually means half a year. The value of “n” would be 2 for interest compounded semi-annually.
Annually
For annually, “n” is 1 as annually means once a year as in figure 3.
The value of “n” only divides the annual interest over the specific period which is compounded.
Figure 5 shows a 12% annual interest division over different time periods. The interest rate decreases with the increased period divisions annually.

Figure 5 – Division of Annual Interest Over Different Time Periods
Continuously Compounded Interest
For continuously compounded interest, the following formula is used:
A = P. $e^{Rt}$
Notice that this formula does not have the “n” factor as it is not for annual compounding over a period.
This shows constant compounding as the exponential function keeps on increasing until specified by the time t in years.
Interest Compounding Example
Ali deposits $40,000 in his savings account with a 10% annual interest rate compounded semi-annually.
How much money will be accumulated in the account after 20 years at this interest rate?
Solution
The word “semi-annually” in the problem refers to the formula for periodic compounded interest. The formula is given as:
\[ A = P { \Big[ 1 + \frac{R}{n} \Big] }^{nt} \]
Here, the initial principal amount P deposited in the account is $40,000.
The interest rate R is 10% or 10/100 = 0.1 and the number of times the interest is received in a year is semi-annually, so “n” is 2.
The time t passed on the initial deposit is 20 years. Placing the values in the formula gives:
\[ A = 40,000 { \Big[ 1 + \frac{0.1}{2} \Big] }^{2(20)} \]
A = 40,000 $[ 1 + 0.05 ]^{40}$
A = 40,000 $[ 1.05 ]^{40}$
A = 40,000(7.039988)
A = 281,599.5
The final amount after 20 years compounded semi-annually at the 10% annual interest rate will be approximately $281,600.
All the images are created using GeoGebra.
