Computation|Definition & Meaning

Computation is the process of performing mathematical operations such as addition, subtraction, multiplication, and division to obtain a numerical result. 

The process of computation can be carried out manually, with the assistance of a calculator, or by using computer software.

Figure 1: Computation is carried out manually, calculator, or by using computer software.

Numerical Computation

The use of computers to find solutions to problems involving real numbers is what is meant by the term “numerical computation.”

During this process of finding a solution to an issue, there are a few stages that stand out from the others more or less clearly. The first step is the formulation of the plan.

When developing a mathematical model of a physical scenario on a computer, scientists need to keep in mind that they want to use that model to find a solution to a problem at some point in the future. As a result, they will provide for defined objectives, appropriate input data, adequate checks, as well as the type and amount of output they desire.

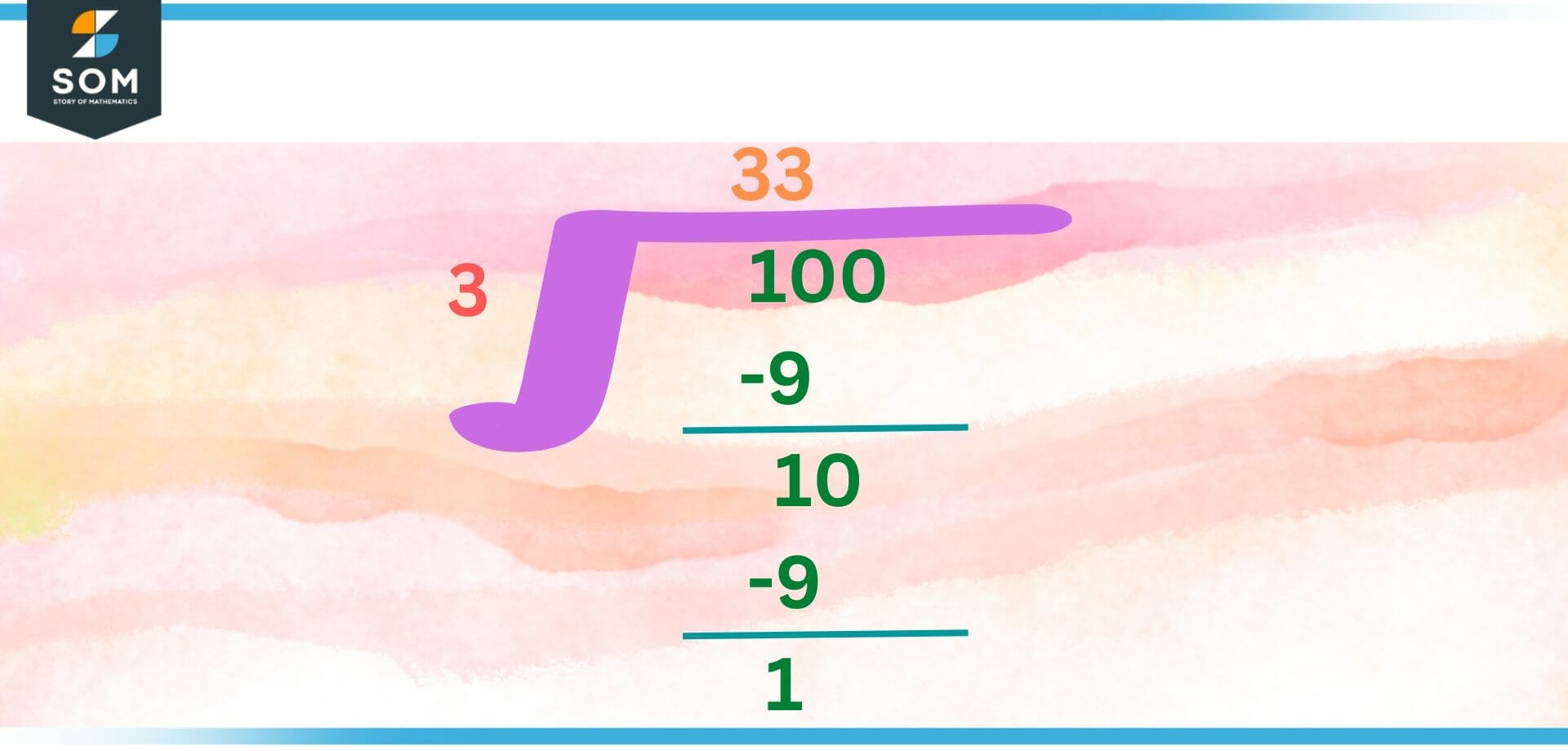
Figure 2: Long division in numerical computation

When a problem has been stated, the next step in the process is to create the numerical methods that will be used to solve the problem, along with a first error analysis. An algorithm is a specific kind of computational procedure that may be applied to the solution of a problem.

An algorithm is a comprehensive and unambiguous collection of steps that may be applied to the solution of a mathematical issue. Algorithms are used to find the answer to mathematical problems. Numerical analysis is utilized to assist in the process of selecting or constructing effective algorithmic solutions.

In order to solve the issue, we need to settle on a particular method or collection of algorithms; in addition, numerical analysts need to take into account all of the potential error sources that could have an impact on the outcomes. They need to think about the level of precision that is expected.

To find a suitable step size or the required number of iterations, evaluate the magnitude of the round-off and discretization errors, and determine an appropriate step size.

The suggested algorithm ought to be converted by the programmer into a set of unambiguous instructions for the computer, which are then carried out in the appropriate order. The first thing you’ll do in this process is look at the flow chart.

A flow chart is nothing more than a list of steps, which are typically presented in the form of logical blocks that the computer is intended to carry out.

The level of difficulty of the flow will be proportional to the level of difficulty of the problem as well as the amount of detail that is presented. However, it should be possible for someone other than the programmer to follow the flow of information from the chart. This is because the programmer is the only person who should be able to do it.

A flow chart is a helpful tool for programmer; nonetheless, they are required to translate the flow chart’s primary functions into a computer program. In addition to this, it serves as an efficient method of communication with people who are interested in comprehending the functions that are performed by the program.

Characteristics of Numerical Computing

Accuracy: Every single numerical procedure has the potential to generate errors. It’s possible that the reason is due to the correct mathematical technique being used or that it’s because the computer is accurately representing and changing the numbers.

Efficiency: Another factor to take into account when picking a numerical approach for solving a mathematical model is its level of efficiency. Efficiency means the amount of work that must be done in order for the approach to be utilized by either people or computers.

Numerical instability: Numerical instability is another issue that arises when using a numerical method, and it’s important to be aware of this. Any errors that are factored into the calculation, regardless of where they came from, will increase it in some way. These errors often occur very quickly, which can lead to disastrous outcomes in some circumstances.

Process of Numerical Computing 

• The mathematical model construction.
• The development of an acceptable numerical system.
• The actual application of a solution.
• The solution is checked for accuracy.

Numerical Method

The term “Numerical Method” refers to a collection of strategies that can be utilized to approximate the steps involved in mathematical procedures. We are forced to resort to approximations either because we are unable to solve the procedure analytically or because the analytical method is too difficult to solve (an example is solving a set of a thousand simultaneous linear equations for a thousand unknowns).

Different Kinds of Numerical Methods

Numerous instruments are at the disposal of numerical analysts and mathematicians, which they put to use in the process of formulating numerical approaches to the resolution of mathematical issues. Changing a given problem into a “near problem” that can be readily solved is the most significant concept, which was described before and is applicable to all different kinds of mathematical problems. This principle cuts across all types of mathematical difficulties.

There are many more concepts, which vary depending on the kind of mathematical issue that is being solved.

An Introduction to Numerical Methods for Solving Common Division Problems the Solutions to the Following Common Division Problems Are Given Below:

• The simplest method for solving ODEs is the Euler method.
•  clear and vague methods must solve the problem at every step
• The clearest variation from the Euler approach is the Euler Back Road.
• The direct method of the second system is the trapezoidal law.
• One of the two major groups of first value problems is the Runge-Kutta method.

Newton Method

There are some equations that cannot be resolved using algebra or any of the other methods available in mathematics. To accomplish this, we use numerical approaches. One of these methods is called Newton’s method, and it enables us to compute the answer to the equation f (x) = 0.

Simpson Law

The value of the other significant ones cannot be determined using integration rules or fundamental functions. Simpson’s law is a mathematical formula that determines the total value of a direct combination based on its component parts.

Trapezoidal Law

Calculating the numerical value of a direct combination can be done with the help of a numerical method known as the trapezoidal rule. The value of the other significant ones cannot be determined using integration rules or fundamental functions.

Non-numerical Computation

A non-numerical computation is a type of computation that does not require standard numerical methods and computations but rather deals with various kinds of information and data. This style of computation is referred to as a “non-numerical computation.”

Symbolic computation, graph theory, logic and reasoning, and string manipulation are a few examples of different types of computation that are not numerical.

Figure 3: Different Algebraic Expressions that can be solved in non-numeric computation

The process of manipulating mathematical symbols and expressions in a manner that is consistent with the principles of algebra and calculus is known as symbolic computation. It is put to use in computer algebra systems (CAS) to carry out algebraic manipulations and make formulas easier to understand.

The study of graphs and networks is the focus of the mathematical field of graph theory, which is a subfield of mathematics. In the field of computer science, it is employed for a variety of purposes, including problem-solving, data analysis, and network optimization.

The non-mathematical style of computation, known as logic and reasoning, entails the formalization and manipulation of logical assertions and arguments. Logic and reasoning are often used interchangeably. For the sake of problem-solving, decision-making, and the representation of knowledge, it is utilized in the fields of artificial intelligence, computer science, and philosophy.

The term “string manipulation” refers to the process of manipulating and analyzing strings of characters, including but not limited to words, phrases, and complete sentences. Pattern recognition, the processing of text, and the analysis of data are all examples of applications for this kind of computation in the fields of computer science and software engineering.

A wide variety of information and data that does not utilize typical numerical methods and calculations are the focus of non-numerical computing. Non-numerical computing is crucial to the study of a wide variety of subfields within computer science and mathematics, including symbolic computation and graph theory, logic and reasoning, and the manipulation of string data.

Conclusion