Cosine|Definition & Meaning

Visual Understanding 

Consider a right triangle ABC. Say side AB is the base of the triangle, Side BC is perpendicular, and side AC is Hypotenuse, then we can define Cosine as the ratio of Side AB and side AC. In other words, the ratio of a triangle’s base to its hypotenuse is referred to as Cosine, which is visually represented as follows.

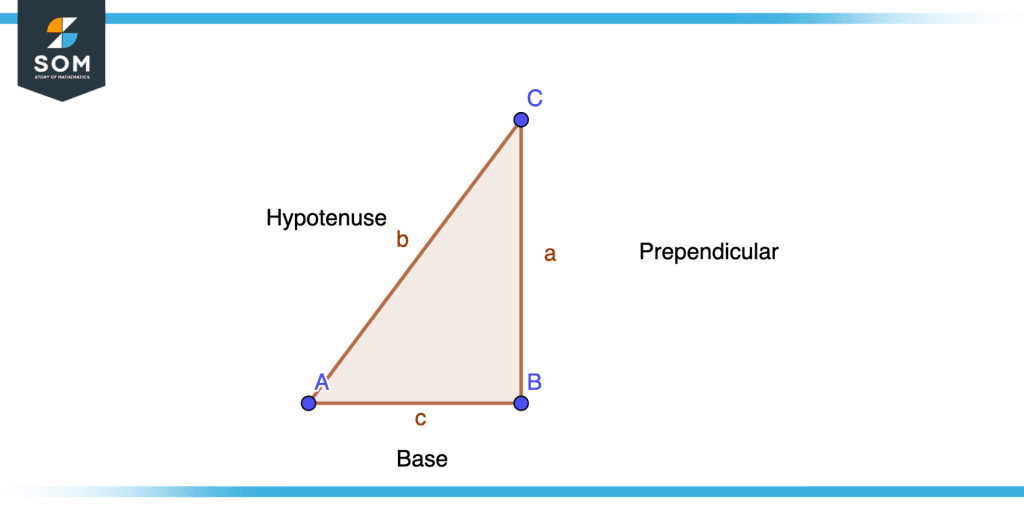
Figure 1 – Visual Understanding of Cos Function

AB=Base of Triangle

BC=Prependicular

AC=Hypotenuse

$\cos\alpha=\dfrac{Base}{Hypotenuse} $

Mathematical Formula

From the above figure, we know that the Base is equal to side AB and Hypotenuse is equal to side AC so we can write

$\cos\alpha=\dfrac{AB}{AC} $

Properties of Cosine

Property 1

In the quadrants the positivity and negativity of cosine changes as it moves from first to second and second to third and from third to fourth. The positive range for the Cosine function lies in quadrant 1 and quadrant 4 whereas the negative range lies in quadrants 2 and 3 as shown in the figure.

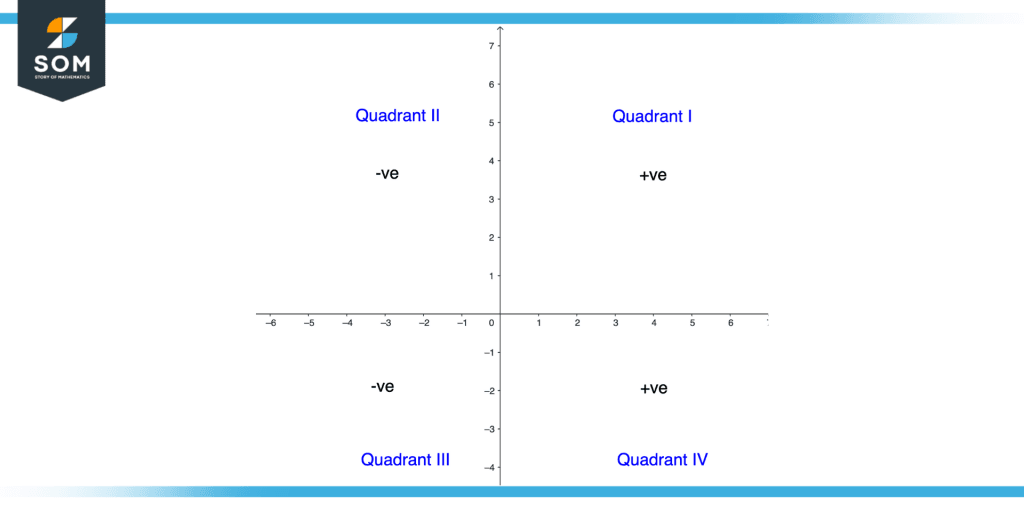
Figure 2 – Cos Positivity and Negativity in Quadrants

In order to verify the property, we will use a calculator.

• In Quadrant 1

$\theta $ ranges from 0 to 90 degrees so we will apply cosine to the lower limit and upper limit of quadrant 1.

Lower Limit: $\theta=0 $, $\cos(0)=1$

Upper Limit: $\theta=90$, $\cos(90)=0$

• In Quadrant 2

$\theta $ ranges from greater than 90 degrees to 180 degrees so we will apply cosine to the lower limit and upper limit of quadrant 2.

Lower Limit: $\theta=91 $, $\cos(91) = -0.0174$

Upper Limit: $\theta=180 $, $\cos(180) = -1$

• In Quadrant 3

$\theta $ ranges from greater than 180 degrees and smaller than 270 degrees so we will apply cosine to the lower limit and upper limit of quadrant 2.

Lower Limit: $\theta=91 $, $\cos(91) = -0.0175$

Upper Limit: $\theta=269 $, $\cos(269) = -0.0174$

• In Quadrant 4

$\theta $ ranges from 270 degrees to 360 degrees so we will apply cosine to the lower limit and upper limit of quadrant 2.

Lower Limit: $\theta=270 $, $\cos(270)=0$

Upper Limit: $\theta=360 $, $\cos(360)=1$

This property is visually illustrated in the figure below.

Property 2

The derivative of cosine is equal to the negative of the sine function. In other words, Cos is the complement of sin

$\dfrac{d}{dx}(\cos(x))=-\sin(x) $

Property 3

The integration of the cosine function gives the sine function.

$\int \cos(x) dx=\sin(x) + C$

Property 4

The cos function is a periodic function.

$\cos\alpha=\cos(\alpha + 2p)$

Property 5

The cos function is an even function.

$\cos(-\alpha)=\cos(\alpha)$

Property 6

Trignometry formulas for two angles, a and b, can be written as

$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$

$\cos(a-b)=\cos(a)\sin(b)+\sin(a)\cos(b)$

Graphical Representation of Cosine Graph

The cos graph starts from 90 degrees and repeats itself after every 360 degrees.+1 and -1 are the maximum and minimum values in the graph of Cos. There is a slight difference between the sin and cos graphs where the sin graph crosses or sweeps the origin whereas the cos graph never does so. The graph for cosine is shown in the figure below.

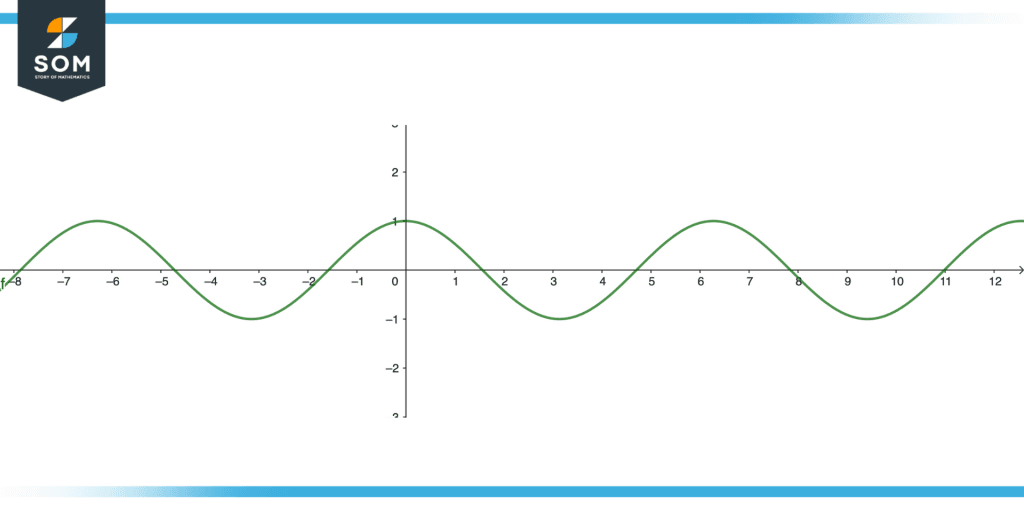
Figure 3 – Cos Function Graph

Properties of Cos Graph

1. The graph of cosine never sweeps from the origin point.
2. For every positive and negative value of theta, the cos graph maintains its continuity and repeats after every 360 degrees.
3. The amplitude of the cos graph can be referred to as 1 with positive 1 being the maximum value and negative 1 being the smallest value.

Law of Cosines

A triangle’s side lengths are related to one of its angles through the law of cosines. The use of trigonometry allows us to measure distances and angles that can’t be calculated any other way. When we know two sides and the enclosed angle of the triangle, we can apply the law of cosines to compute the third side.

In a triangle, the cosine of its angles and the length of its sides can be determined by the law of cosine. In trigonometry, a right triangle is represented by the cosine law, which generalizes Pythagoras’ theorem.

Statement

Consider a triangle with sides x, y, and z. Then the square of one of the sides, say z, is equal to the difference between the sum of squares of side x, and side y and two times the product of side x and side y and angle between them.

$z^{2}=x^{2}+y^{2}-2xy\cos(Z)$

The cosine rule is another name for the law of cosine. Any triangle can be solved with the help of this law. This rule can be used, for example, to find the third side of a triangle when you know the lengths of two sides and the degree included between them. The illustration is shown in the figure.

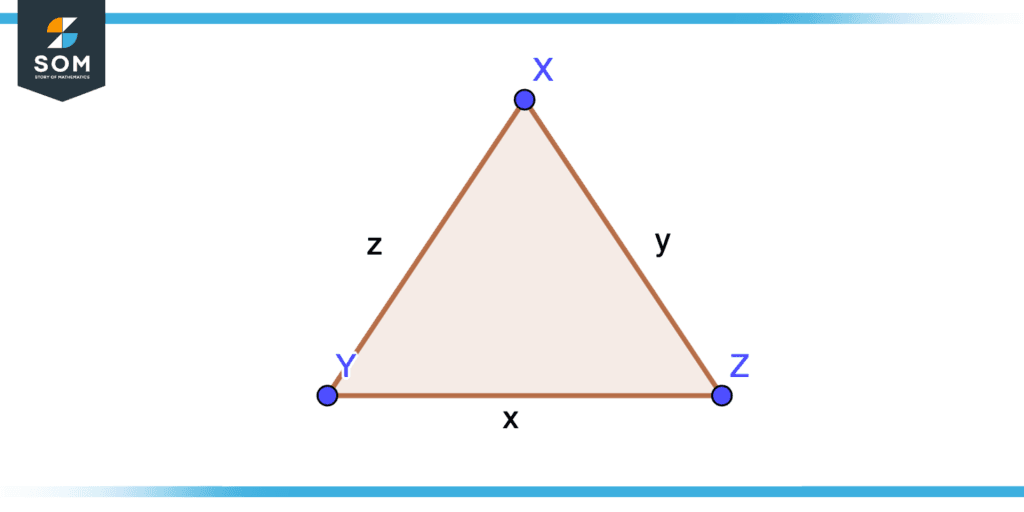
Figure 4 – Illustration of Law of Cosines

Formula

There are three laws of cosines. Consider a triangle having three sides x, y and z. In order to find:

• Side x, when side y, z is given along angle X

\[x^{2}=y^{2}+z^{2}-2yz\cos(X)\]

• Side y, when side x, z is given along angle Y

\[y^{2}=x^{2}+z^{2}-2xz\cos(Y)\]

• Side z, when side y, z is given along angle Z

\[z^{2}=x^{2}+y^{2}-2xy\cos(X)\]

Properties

1. The Law of cosines is used to find an unknown side of triangle when two other triangles are given.
2. The Law of cosines is used to find the angle between the sides when all three sides are given.
3. The Law of cosines is not limited to just right-angle triangles it can be easily applied to any other triangle whose sides or angles are to be found.

Solved Examples With the Cosine Function

Example 1

Consider four values of theta and compute the cos function for all the values of theta using the calculator.

Solution

$\theta=0,90,180,270,360$

$\cos(0)=1$

$\cos(90)=0$

$\cos(270)=0$

$\cos(360)=1$

Example 2

Consider a triangle ABC with side AC=2 AB=5 BC=$\sqrt2$ Find the angle $\alpha$. The figure from this problem is shown below.

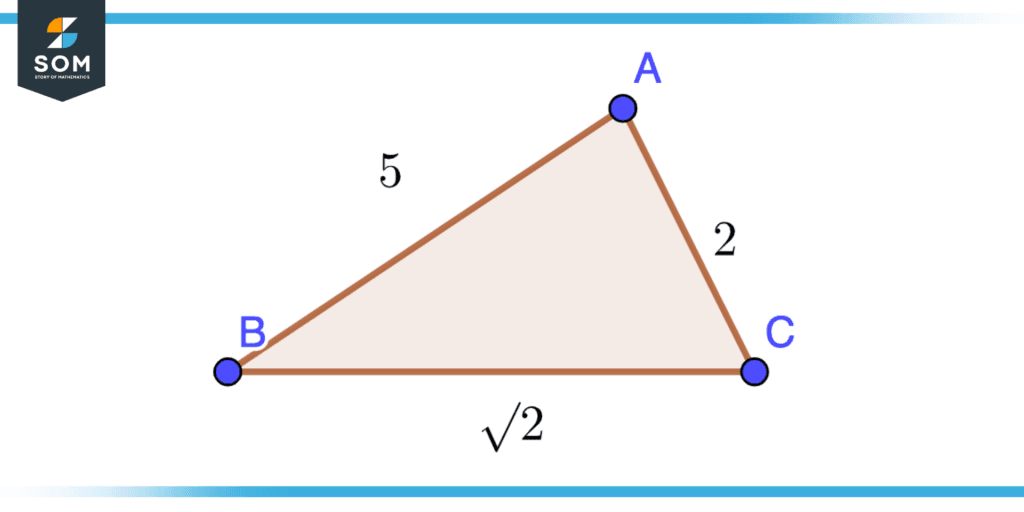
Figure 5 – Cos Function Example

Solution

$\cos\alpha=\dfrac{Base}{Hypotenuse} $

$\cos\alpha=\dfrac{BC}{AB} $

$\alpha=\arccos\dfrac{\sqrt2}{5} $

$\alpha=73.57^{\circ}$

Example 3

Consider the following triangle with side AB=4 BC=5 AC=6 and finds the angle A. The figure from this problem is shown below.

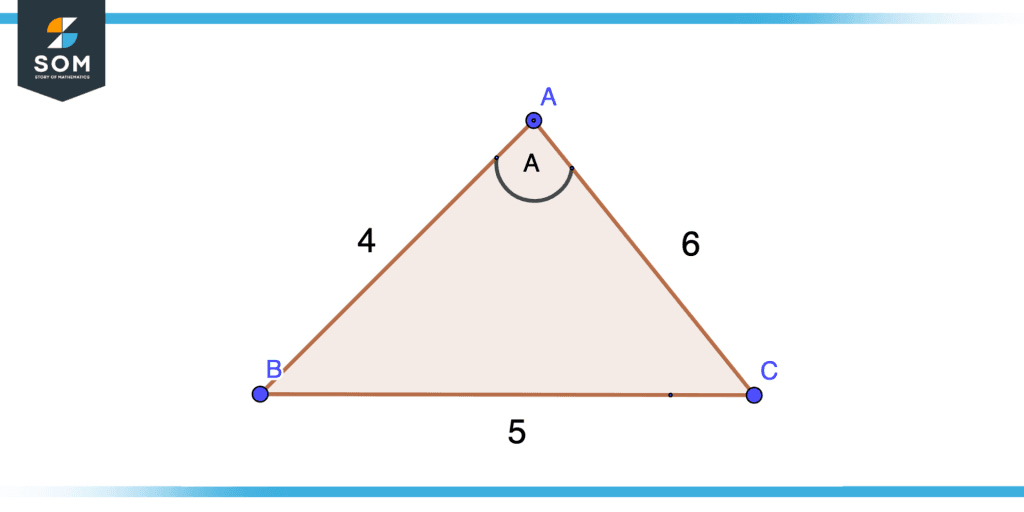
Figure 6 – Law of Cosine Example

Solution

Applying the law of cosines:

$a^{2}=b^{2}+c^{2}-2bc\cos(A)$

$5^{2}=6^{2}+4^{2}-2.6.4\cos(A)$

$25=36+16-48 x \cos(A)$

$-48\cos(A)=-27$

$\cos(A)=\dfrac{-27}{-48}$

$\cos(A)=0.5625$

$A=\arccos0.5625$

$A=55.77^{\circ}$

All mathematical drawings and images were created with GeoGebra.

Cosh Definition < Glossary Index > Cosine Rule Definition