Cosh|Definition & Meaning

In applied mathematics, hyperbolic functions are equivalents of regular trigonometric functions but expressed by means of the hyperbola instead of a circle. 

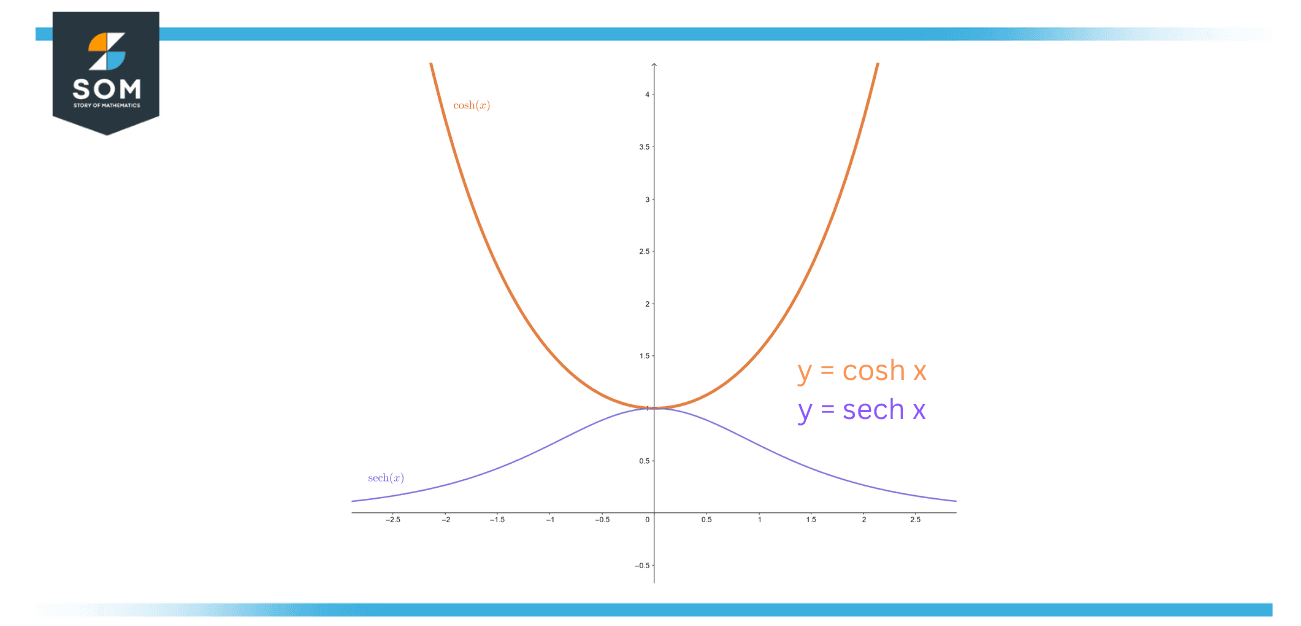
Figure 1 – Graph of cosh x and sech x

Here we are going to look into the cosh (x), which is defined by the formula given below:

\[\cosh(x) = \dfrac{e^x + e^{(-x)}}{2} \]

In applied mathematics, the exponential functions are used in a variety of even and odd combinations that deserve to be given their own names. These hyperbolic functions are similar in many ways to the trigonometric functions because of their association with the hyperbola in the form of a circle.

Because of this, they are communally termed hyperbolic functions and separately termed hyperbolic sine, hyperbolic cosine, and so forth.

What Are Trigonometric Functions?

Looking at a right-angled triangle, the side that is opposite to the right angle is known as the hypotenuse, and if we choose one other angle and name it θ theta, then the other remaining sides are usually labeled as the opposite side, and the adjacent side (the side next to θ). The ratio of any two sides, like adjacent/ hypotenuse, will constitute a function with a special name, the cosine of theta or cos (θ).

Cos(θ) = $\dfrac{\textsf{adjacent}}{\textsf{hypotenuse}}$

Similarly, considering the other possible ratios, we can construct the other trigonometric functions:

Sin(θ) = $\dfrac{\textsf{opposite}}{\textsf{hypotenuse}}$

Tan(θ) = $\dfrac{\textsf{opposite}}{\textsf{adjacent}}$

The cosine can be defined using a visual representation by considering a circle of diameter 2, having center O at the origin inside the (x, y) plane. Consider point A on the edge of the circle having the coordinates (1, 0). Now the distance from that point to the origin is called as OA and has a length of 1 unit.

Let there be another point P on the line of the circle’s arbitrary coordinates (a, b). The angle between the two lengths, OA and OP, is defined by θ. Here theta is the radian representation.

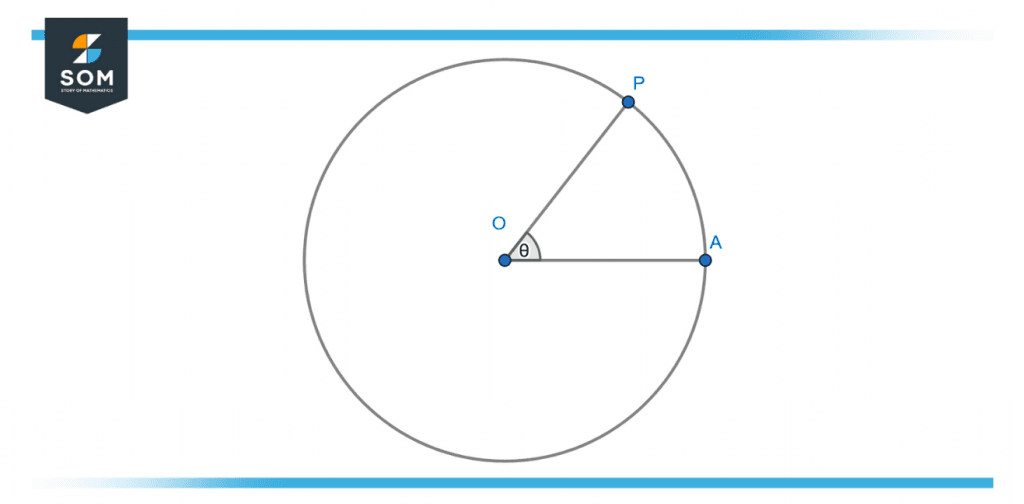
Figure 2 – A circle of unit radius

In simpler terms, the cosine of θ is described as the projection of P on the x-axis.

What Are Hyperbolic Functions?

In applied mathematics, hyperbolic functions are equivalents to regular trigonometric functions but expressed by means of the hyperbola instead of a circle. While the points (cos t, sin t) are derived from a circle having a unit radius, the functions (cosh t, sinh t) develop the rightmost half of the unit hyperbola.

Their derivatives are also similar to the derivatives of trigonometric functions, except the sign. We know the derivatives of sin(t) and cos(t) are, respectively, cos(t) and –sin(t), while the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t).

Hyperbolic functions arise where one needs to compute angles and distances in hyperbolic geometry. They are also used in various solutions of linear differential equations, cubic functions, and Laplace’s equation. Laplace’s equations are significant in numerous fields of physics, which include electromagnetic concepts, heat fusion, etc.

All the hyperbolic functions acquire a real value termed a hyperbolic angle. The hyperbolic angle is double the size of the area of the hyperbolic segment it is constructed in.

Defining Hyperbolic Cosine

We can draft the graph for hyperbolic cosine by utilizing the given information of the exponential $e^x$ and $e^{−x}$. Initially, let us compute the value of cosh 0 by taking x = 0. Thus, the exponents become $e^x$ = 1 and $e^{−x}$ = 1. Thus:

\[\cosh(x) = \dfrac{e^0 + e^{(-0)}}{2} \]

= (1 + 1) / 2 = 1

Rewriting the cosh x to determine the change when the value of x gets large:

\[\cosh(x) = \dfrac{e^{x/2} + e^{x/2}}{2} \]

The graph below shows the behavior of the exponential when x gets large.

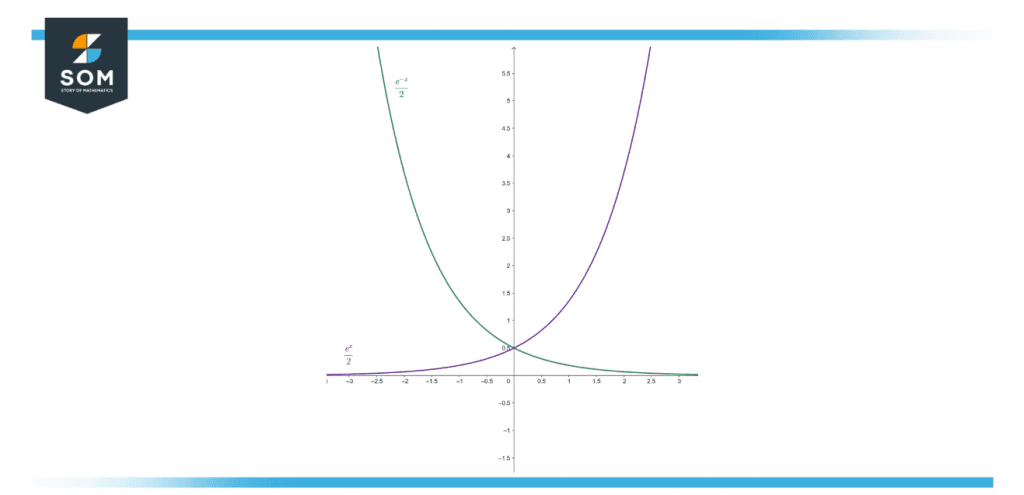
Figure 3 – Graph of $e^x$ and $e^{-x}$

Looking at the graph, the positive exponential increases quickly when x gets larger, but the negative exponential decreases rapidly with the change in x. So as the x gets larger, the hyperbolic cosine gets closer and closer to the positive exponential, i.e., $e^{x/2}$:

$\cosh x = e^{x/2}$   for larger values of x

The graph of cosh x will eventually remain above the graph of the $e^{x/2}$ due to the fact that the second part of the function, despite being very small, will always be greater than zero. As the value of x gets bigger and bigger, the difference in both graphs gets minor and minor.

Now, Let’s say that the value of x becomes more and more negative, the positive exponential will fall drastically, but the negative exponential increases rapidly with the negative change in x. So as the x gets smaller and smaller, the hyperbolic cosine gets closer and closer to the negative exponential, i.e., $e^{-x/2}$:

$\cosh x = e^{-x/2}$   for large negative values of x

Even if the x is negative, the graph of cosh x will ultimately remain above the graph of the $e^{-x/2}$ because the first part of the sum, regardless of being very small, will always be greater than zero. As the value of x gets smaller and smaller, the difference in both graphs gets negligible.

Thus, we can construct the graph for cosh x. One thing to observe is that the graph is symmetrical about the y-axis because cosh x = cosh (-x), as described above.

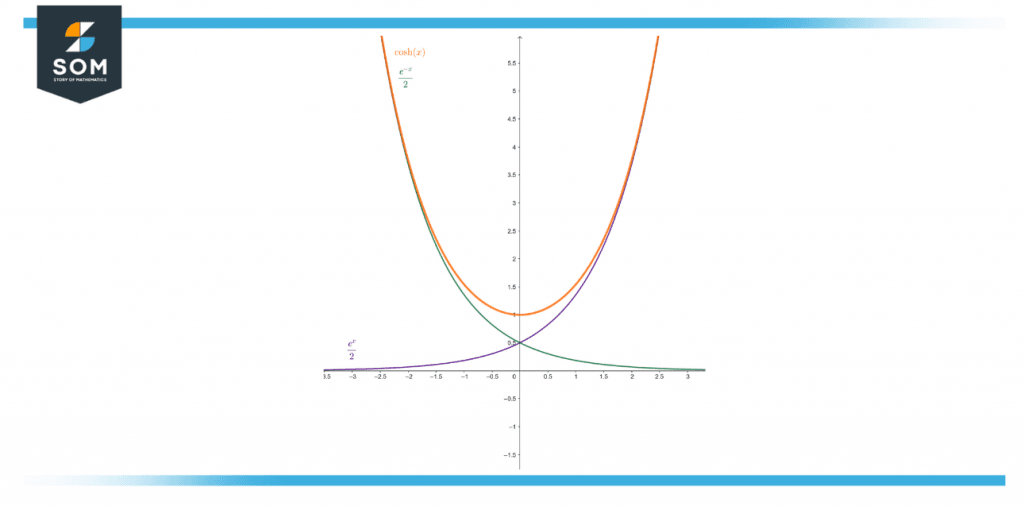
Figure 4 – Graph showing the hyperbolic cosine

Important Identity of cosh

Cosh, along with sinh, have various identities that look analogous to identities for the regular trigonometric functions of cos and sin, with a slight change in the signs. The identity looks like this:

\[\cosh^{2} x-\sinh^{2} x = 1\]

We can recall the trigonometric identity similar to the one above $\cos^2 x + \sin^2 x = 1$, with the plus sign changing to minus.

The identity given above can effortlessly be drawn from the fundamental definitions as follows:

\[\cosh^{2} x-\sinh^{2} x = \dfrac{e^x + e^{(-x)}}{2}-\dfrac{e^x – e^{(-x)}}{2}\]

\[= \dfrac{e^{2x} + e^{-2x}}{4}-\dfrac{e^{2x}-e^{(-2x)}}{4}\]

\[= \frac{1}{2}-\frac{-1}{2}\]

\[= 1\]

Another important identity to look for is:

Sinh(x + y) = sinh x cosh y + cosh x sinh y

Osborn’s Rule

Osborn’s rule implies that the trigonometric identities can be converted to their corresponding hyperbolic identities by replacing all occurrences of sins and cosine with their counter hyperbolic sine and cosine. Also, if them occurs a product of two sines, the corresponding hyperbolic product will have a negative sign.

For instance, $\cos(2A) = 2\cos^2(A)-1$ will be changed into $\cosh2A = 2\cosh^2(A)-1$ whereas,

\[\cos(2A) = 1-\sin^2(A) \Rightarrow \cosh(2A) = 1+\sinh^2(A)\]

In order to apply Osborn’s rule on other trigonometric identities, they must first be narrowed down to sines and cosines.

Solved Example

For the equation 5 cosh x + 3 sinh x = 4, solve for x.

Solution

Using the basic definitions of cosh and sinh, the given equation can be written as:

\[5 \dfrac{e^x + e^{(-x)}}{2} + 3 \dfrac{e^x + e^{(-x)}}{2} = 4\]

Simplifying it gives us the following:

\[4e^x + e^{-x} = 4\]

Multiplying by $e^x$ gives:

\[4e^{2x} + 1 = 4e^x\]

Rewriting this forms a quadratic equation:

\[4e^{2x}-4e^x + 1 = 0\]

Solving the quadratic equation gives:

\[e^x = \dfrac{1}{8} (4 \pm \sqrt{0})\]

\[e^x = \dfrac{1}{2}\]

Hence:

\[x = \ln\left(\frac{1}{2}\right)\]

\[= \ln 2^{-1}\]

\[= -\ln2\]

All images/mathematical drawings were created with GeoGebra.

Correlation Definition < Glossary Index > Cosine Definition