JUMP TO TOPIC
Counting Number|Definition & Meaning
Definition
Any number except zero that we can use to count things is called a counting number. This means that the number cannot be negative, it cannot be a fraction, and it cannot be a decimal. Therefore, the infinite set {1, 2, 3, …} represents all the counting numbers. The set of natural numbers is equivalent to the set of counting numbers in most contexts.
Counting numbers from 1 to 10 have been depicted in Figure 1 below:

Figure 1: Counting numbers from 1-10
Counting numbers, also known as natural numbers, are a set of positive integers used to represent the number of elements in a set or collection. They are the numbers that we use to count objects or quantities, such as the number of apples in a basket or the number of people in a room. Counting numbers start at 1 and go on indefinitely, and each number represents one more than the number before it (e.g., 1, 2, 3, 4, etc.).
The fundamental skill we begin learning in kindergarten is how to count.
This is employed in daily life as well. Example,
- Give the time indicated by the clock.
- Counting the students in the room
- purchasing a variety of toffees, etc.
Both even and odd numbers are included in counting numbers. For example, 6 – even number and 9 – odd number. The numbers can be counted in a variety of ways, for instance:
- Counting by 2 – 2, 4, 6, …
- Counting by 3 – 3, 6, 9, …
- Counting by 4 – 4, 8, 12, …
- Counting by 5 – 5, 10, 15,…
- Counting by 6 and so on.
The set of counting numbers is usually represented by the symbol N or sometimes by the symbol Z^+. The set of counting numbers is infinite and does not include negative numbers, zeros, or fractions. They are the foundation of the number system and are used to perform basic mathematical operations such as addition, subtraction, multiplication, and division.
It is important to note that counting numbers do not include negative numbers, zeros, or fractions. They start at 1 and go on indefinitely. They can be used to count and organize any set of distinct objects, quantities, or concepts.
The counting numbers can be organized in a number system, where counting numbers are the positive integers, and the operations of addition, subtraction, multiplication, and division can be applied to them. The set of counting numbers is infinite, and it is one of the most basic concepts in arithmetic and is a foundation for many branches of mathematics.
The purpose of counting numbers is to provide a way to quantify and organize the elements of a set or collection. They are used to measure and compare quantities and to perform arithmetic operations such as addition, subtraction, multiplication, and division. Counting numbers are also used as the basis for many mathematical concepts and structures, including number theory, combinatorics, and algebra.
In addition to that, counting numbers also play a fundamental role in many fields, such as computer science, cryptography, and probability theory. For example, in computer science, counting numbers are used to represent the number of elements in a data structure, while in cryptography, counting numbers are used to represent the number of possible keys.
In summary, counting numbers provide a way to measure and organize quantities, and they play a fundamental role in many areas of mathematics and its applications.
Types Of Counting Numbers
There are several types of numbers that are commonly used in mathematics, including:
- Natural numbers: These are the counting numbers or positive integers that are used to count the number of elements in a set or collection. They are represented by the symbol N or sometimes by the symbol Z^+.
- Integers: These are numbers that include both natural numbers and their negatives, but not fractions or decimals. They are represented by the symbol Z.
- Rational numbers: These are numbers that can be expressed as the ratio of two integers, such as fractions or decimals that terminate or repeat.
- Irrational numbers: These are numbers that cannot be expressed as the ratio of two integers, such as the square root of 2 or pi.
- Real numbers: These are numbers that include all rational and irrational numbers.
- Complex numbers: These are numbers that include a real part and an imaginary part, represented by the symbol i, which is the square root of -1.
- Transcendental numbers: These are numbers that are not algebraic numbers, meaning they cannot be the root of any non-zero polynomial equation with integer coefficients.
These are the main types of numbers, but there are also different classifications of numbers based on their properties or characteristics.
Classification of Counting Numbers
There are different ways of classifying counting numbers based on their properties or characteristics. Some types are given below:
Prime numbers: These are counting numbers that are divisible only by 1 and themselves. Examples are 2, 3, 5, 7, 11, etc.
Composite numbers: These are counting numbers that are divisible by more than one positive integer. Examples are 4, 6, 8, 9, etc.
Perfect numbers: These are counting numbers that are equal to the sum of their divisors, excluding themselves. Examples are 6 and 28
Happy numbers: These are counting numbers that are defined by a specific set of rules and are said to be “happy” when they follow those rules.
Triangular numbers: These are counting numbers that can be represented by the form n*{(n+1)/2} where n is a natural number.
So, counting numbers are not classified into different types, but different properties of numbers can be used to classify them.
Uses And Advantages of Counting Numbers
- Measuring and quantifying: Counting numbers are used to measure and quantify the number of elements in a set or collection. They provide a way to count and organize objects or quantities, such as the number of apples in a basket or the number of people in a room.
- Arithmetic operations: The basis of the number system, counting numbers are used to carry out fundamental mathematical operations like addition, subtraction, multiplication, and division.
- Mathematical concepts and structures: Counting numbers are used as the basis for many mathematical concepts and structures, including number theory, combinatorics, and algebra.
- Applications: Counting numbers play a fundamental role in many areas of mathematics and its applications, such as computer science, cryptography, and probability theory.
- Counting and Number theory: Counting problems often lead to number theoretical solutions. For example, counting the number of ways to partition a number into smaller numbers is related to the study of partitions of integers in number theory.
- Simplicity: Counting numbers are simple to understand and use. The concept of counting numbers is one of the first concepts that children learn in math, and it is a foundation for many other mathematical concepts.
- Versatility: Counting numbers are versatile, as they can be used in many different fields and for many different purposes. They can be used to count and measure anything from physical objects to abstract concepts, and they can be used in both simple and complex mathematical problems.
Overall, counting numbers are a fundamental concept in mathematics and have many uses and advantages across many fields.
Numbers 1–10 on Fingers
Children can learn and assimilate the basic characteristics of natural numbers by representing numbers with finger configurations. The illustration below demonstrates how we can represent the numerals from one to 10 with our fingers.

Figure 2: Counting numbers using fingers
Names of Numbers 1 to 20
The names of the numerals from 1 to 20 are shown in the following table.
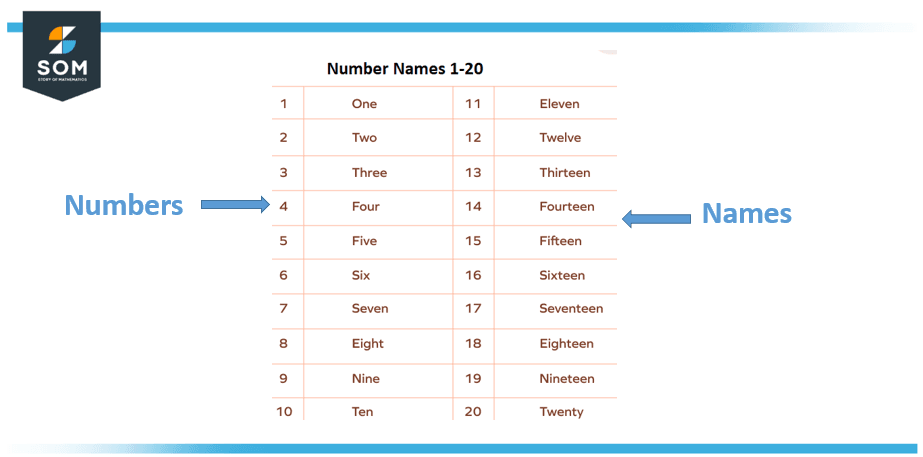
Figure 3: Names assigned to numbers.
Different Methods of Number Counting
The numbers can be counted forward.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, etc.
Numbers can be counted backward.
10, 9, 8, 7, 6, 5, 4, 3, 2, for instance.
You can also utilize skip counting. Skip counting is a technique for counting on other numbers except 1.
- By twos: 2, 4, 6, etc.
- By threes: 3, 6, 9
- 4 times out of 10: 4, 8, 12
Solved Examples of Counting Numbers
Example 1
Give at least five examples of counting numbers from real life
Solution
Some examples of counting numbers from real life include:
- The number of apples in a basket
- The number of people in a room
- The number of pages in a book
- The number of cars in a parking lot
- The number of words in a sentence
- The number of days in a month
Example 2
Write the even counting numbers between 10 to 20.
Solution
Even numbers are divisible by 2.
Counting numbers between 10 to 20: 11, 12, 13, 14, 15, 16, 17, 18, 19
So, even numbers between 10 to 20: 12, 14, 16, 18
All images/mathematical drawings were created with GeoGebra.
