Csch|Definition & Meaning

The hyperbolic functions can be thought of as being analogous to either the trigonometric functions or the circular functions. In most cases, the hyperbolic functions are expressed by the algebraic formulas which involve the exponential term (e^y) and its inverse (e^-y), where e refers to Euler’s constant. There are six hyperbolic functions in total namely cosh (y), sinh (y), tanh (y), coth (y), csch (y), sech (y). Graphical illustration of sinh (y) and tanh (y) are shown below as an example. 

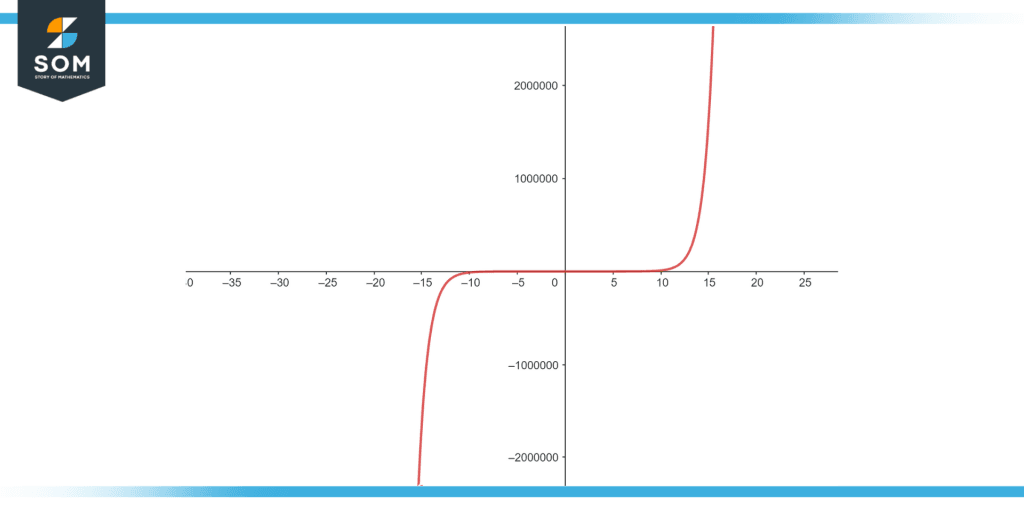
Figure 1: Illustration of Sinh (y)

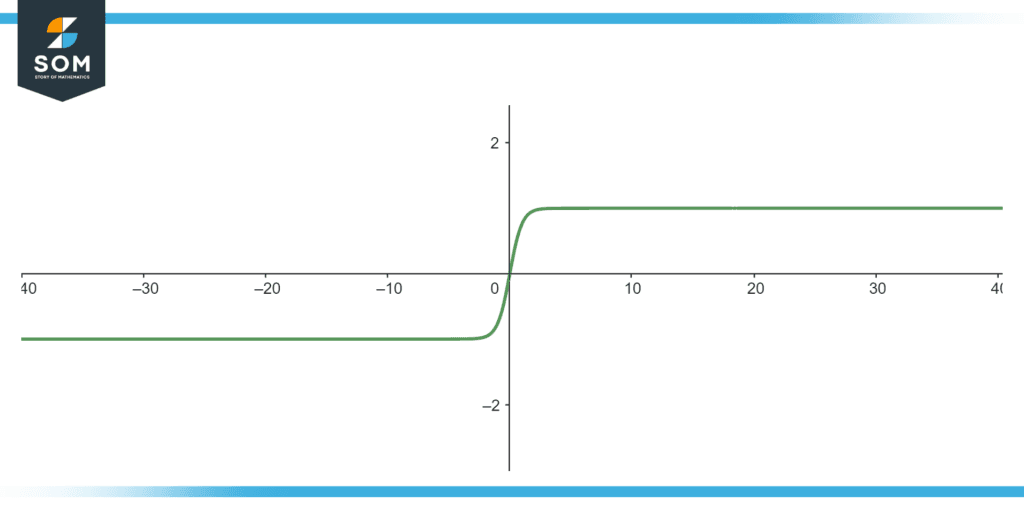
Figure 2: Illustration of tanh (y)

In this article, we will discuss the hyperbolic cosecant function, its properties, characteristics, and its various representations.

What Is a Hyperbolic Cosecant Function?

Hyperbolic cosecant function, abbreviated as csch, is a hyperbolic function. The simplest definition of cosecant hyperbolic function is that it is the inverse form of the hyperbolic sine function. The mathematical form of the relation is shown below.

\[ \operatorname {csch} (y) = \frac {1} {\operatorname {sinh} (y)} = \frac{1} {\frac{e^y – e^{-y}} {2}} = \frac{2}{e^y – e^{-y}} \]

Hyperbolic cosecant of function f (y) = csch (y) is visually illustrated in the below diagram.

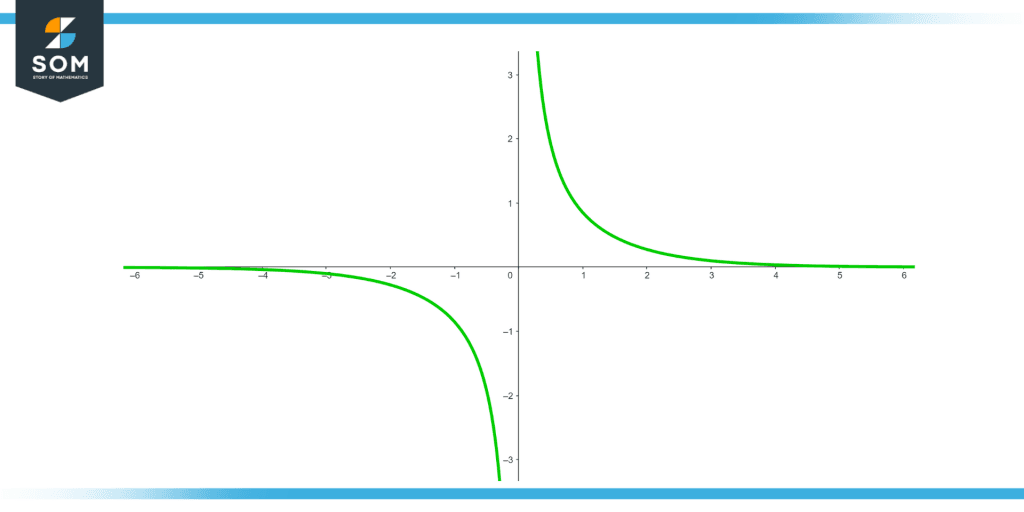
Figure 3: Graphical Representation of Hyperbolic Cosecant Function

Representation via Other Mathematical Functions

We can mathematically describe the hyperbolic cosecant function with some other mathematical functions that are more generic in nature. As we have already seen that the hyperbolic cosecant function could also be described as the inverse of the hyperbolic sine function. Similarly, hyperbolic cosecant can also be described as an inverse of some other special functions as described below:

\[ \operatorname {csch} (\mathrm{y}) = \frac{1} {y_0\left(\begin{array} {ll}3 & y^2 \\ 2 & 2\end{array}\right)} \]

\[ \operatorname {csch} (\mathrm{y}) = \sqrt{\frac {2} {\pi}} \ frac{i} {\sqrt{i \cdot y} \cdot j_{\frac{1}{2}} \cdot(i \cdot y)} \]

\[ \operatorname {csch} (\mathrm{y}) = \sqrt{\frac {2} {\pi}} \frac{i} {\sqrt{y} \cdot j_{\frac {1}{2}} \cdot(y)} \]

\[ \operatorname {csch}(\mathrm{y})=\sqrt{\frac{2}{\pi}} \frac{i}{\sqrt{i \cdot y} \cdot Y_{\frac{1}{2}} \cdot(i \cdot y)} \]

\[ \operatorname {csch}(y) = \sqrt{\frac{2} {\pi}} \frac{i} {\sqrt{y} \cdot j_{\frac{1}{2}} \cdot(y)} \]

\[ \operatorname {csch} (\mathrm{y}) = \frac{\sqrt{\frac{2} {\pi}}} {\sqrt{y} \cdot L_{\frac{1}{2}} \cdot(y)} \]

\[ \operatorname {csch}(\mathrm{y}) =\frac{i} {Se\ (1,0,i,y)} \]

Well-known Characteristics of the Hyperbolic Cosecant Function

Hyperbolic Cosecant Function for Special Values

The results of the hyperbolic cosecant functions against particular numbers of its argument can be determined simply from the related values of the spherical cosecant in the particular points of the circle. These values are as follows:

\[ csch(0) = ∞ \]

\[ csch \binom{\pi i} {2} = -I \]

\[ csch \left(\pi i\right) = ∞ \]

\[ csch \left(\frac{3\pi i} {2}\right) = -I \]

\[ csch \left(\frac{\pi i} {6}\right) = -2i \]

\[ csch \left(\frac{2\pi i} {3}\right) = \frac{2i} {\sqrt3} \]

\[ csch \left(\frac{7\pi i} {6}\right) = -2i \]

\[ csch \left(\frac{5\pi i} {3}\right) = \frac{2i} {\sqrt3} \]

\[ csch \left(\frac{\pi i} {4}\right) = -\sqrt2i \]

\[ csch \left(\frac{3\pi i} {4}\right) = -\sqrt2i \]

\[ csch \left(\frac{5\pi i} {4}\right) = \sqrt2i \]

\[ csch \left(\frac{7\pi i} {4}\right) = \sqrt2i \]

\[ csch \left(\frac{7\pi i} {4}\right) = \sqrt2i \]

\[ csch \left(\frac{\pi i} {3}\right) = -\frac{2i} {\sqrt3} \]

\[ csch \left(\frac{5\pi i} {6}\right) = -\ 2i \]

\[ csch \left(\frac{4\pi i} {3}\right) = \frac{2i} {\sqrt3} \]

\[ csch \left(\frac{11\pi i} {6}\right) = 2i \]

Derivative of Hyperbolic Cosecant Function

The first-order derivative of the hyperbolic cosecant function can be expressed using the hyperbolic cotangent function (coth), as described below:

\[ \frac{\partial\operatorname {csch} {(y)} } {\partial y} = – coth(y) cosch(y) \]

Whereas the n^th order derivative of the Hyperbolic cosecant function can be expressed as shown below:

 $\frac {\partial\operatorname {csch} {(y)} } {\partial y} = \\ cosch(y) \left(\delta_n+\left(n+1\right)!\ \sum_{K=0}^{n}\sum_{j=0}^{\left(\frac{k-1} {2}\right)} \frac{\left(\left({-1}^j\right)i^{-k-n}2^{1-k}\left(k-2j\right)^n{csch}^k\left(y\right)\right) cosh\left(\frac{1}{2} i\pi\left(n-k\right)+\left(k-sj\right)y\right)} {\left(k+1\right)\ j!\left(k-j\right)! \left(n-k\right)!}\ \right) $

Following is the Graphical illustration of derivative of Hyperbolic Cosecant of Function.

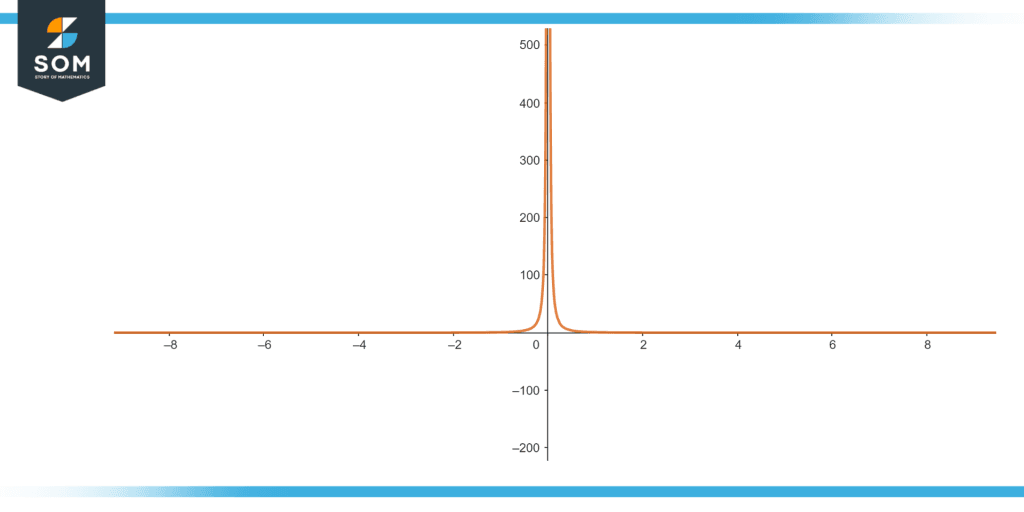
Figure 4: Illustration of Derivative of Cosech

Representation of Hyperbolic Cosecant in Series

Hyperbolic cosecant function can be expressed in the Laurent series expansion in the following manner. The series converges for all the finite numbers y where 0 < |y| < π.

\[ csch = \frac{1} {y} – \frac{y} {6} + \frac {7y^3}{360} – …… = \frac{1} {y} – \sum_{K=1}^{\infty}\frac{2\left(2^{2k-1}-1\right)B_{2k}\ Y^{2k-1}} {\left(2K\right)!} \]

Here 2k represents Bernoulli numbers.

Integral of Hyperbolic Cosecant Function

The hyperbolic cosecant function can also be represented through definite integral through the following equation:

\[ csch(y) = \frac{i} {\pi} \int_{0}^{\infty} {\frac{1}{t^2+t}t^\frac{iy} {\pi}}dt \]

Hyperbolic Cosecant Function of an Addition or a Subtraction

The addition or a subtraction argument of a hyperbolic cosecant function can be expressed using the hyperbolic cosine and hyperbolic sine function as shown in the following equation:

\[ csch (x + y) = \frac{1} {\cosh{(y)}\sinh{\ \left(x\right)+\cosh{\left(x\right)\ } sinh(y)}} \]

\[ csch (x – y) = \frac{1} {\cosh {(y)}\sinh {\ \left(x\right)-\cosh {\left(x\right)\ } sinh(y)}} \]

Hyperbolic Cosecant Function of a Multiple

The hyperbolic cosecant function of multiple arguments such as “2y”, “3y” …… “ny” can be expressed through hyperbolic cosecant functions and hyperbolic secant function. Two examples of this case of multiple argument are shown below:

\[ csch (2y) = \frac{1}{2} csch (y) sech (y) \]

\[ csch (3y) = \frac{{csch}^3\ (y)}{{3csch}^2\ \left(y\right)\ +4} \]

Hyperbolic Cosecant Function of a Half Angle

We can express half angle of hyperbolic cosecant function through the following equation. The equation, however, is only applicable to the horizontal half of the strip:

\[ csch\ \left(\frac{y}{2}\right)\ =\ \frac{\sqrt2}{\sqrt{cosh(y)-1}} \]

For the full horizontal strip, half angle of hyperbolic cosecant function can be expressed through the following equation:

\[ csch\ \left(\frac{y}{2}\right)\ =\ \frac{\sqrt{{2y}^2}}{y\sqrt{cosh(y)-1}} \]

Addition and Subtraction of Direct Functions

We can express the addition of two direct hyperbolic cosecant functions through the following equation:

\[ csch\ (x)\ +\ csch\ (y)\ =\ 2\ sinh\left(\frac{x}{2}\ +\ \frac{y}{2}\right)\ cosh\ \left(\frac{x}{2}\ -\ \frac{y}{2}\right)\ csch\ (x)\ csch\ (y) \]

We can express the subtraction of two direct hyperbolic cosecant functions through the following equation:

\[ csch\ (x)\ -\ csch\ (y)\ =\ -2\ sinh\ \left(\frac{x}{2}\ -\ \frac{y}{2}\right)\ cosh\ \left(\frac{x}{2}\ +\ \frac{y}{2}\right)\ csch\ (x)\ csch\ (y) \]

Multiplication of Direction Functions

We can express the multiplication of two direct hyperbolic cosecant functions through the following equation:

\[ csch\ (x)\ csch\ (y)\ =\ \ \frac{2}{cosh\ (a+b)\ -\ cosh\ (a\ -\ b)\ } \]

We can express the multiplication of hyperbolic cosecant function and hyperbolic secant functions through the following equation:

\[ csch\ (x)\ sech\ (y)\ =\ \ \frac{2}{sinh\ (a\ -\ b)\ +\ sinh\ (a\ +\ b)\ } \]

Applications of Hyperbolic Cosecant Functions

The hyperbolic cosecant function has numerous applications in various scientific fields including the field of mathematics and physics. The hyperbolic cosecant function is also employed in the research and understanding of water and sound waves.

An Example of the Csch Function

Find the derivative of the following function

\[ Z = 5 csch { \left(\frac{Y} {5}\right) } \]

Solution

Since we that:

\[ \frac{\partial} {\partial y}\operatorname {csch} {(y)} = – coth(y) cosch(y) \]

Therefore, we can find the derivative of the given problem as shown below:

\[ \frac{dz} {dy}=5\left(-csch\ \left(\frac{y} {5}\right)coth\left(\frac{y} {5}\right)\right).\frac{1} {5} \]

\[ \frac{dz} {dy}=5\left(-csch\ \left(\frac{y} {5}\right)coth\left(\frac{y} {5}\right)\right).\frac{1} {5} \]

\[ \frac{dz} {dy}=\ -csch\ \left(\frac{y} {5}\right)coth\left(\frac{y} {5}\right) \]

All images/mathematical drawings were created with GeoGebra.

Cross Section Definition < Glossary Index > Cube Definition