JUMP TO TOPIC
Cube Number|Definition & Meaning
Definition
An integer number multiplied by itself three times yields the cube of that number. In other words, the number we get by multiplying the number by itself once, and then once again, is called a cube number.
Cube numbers can be represented visually as a cube, hence the name.
The cube number is called a perfect cube of the number we multiplied to get to it, which is called its cube root.
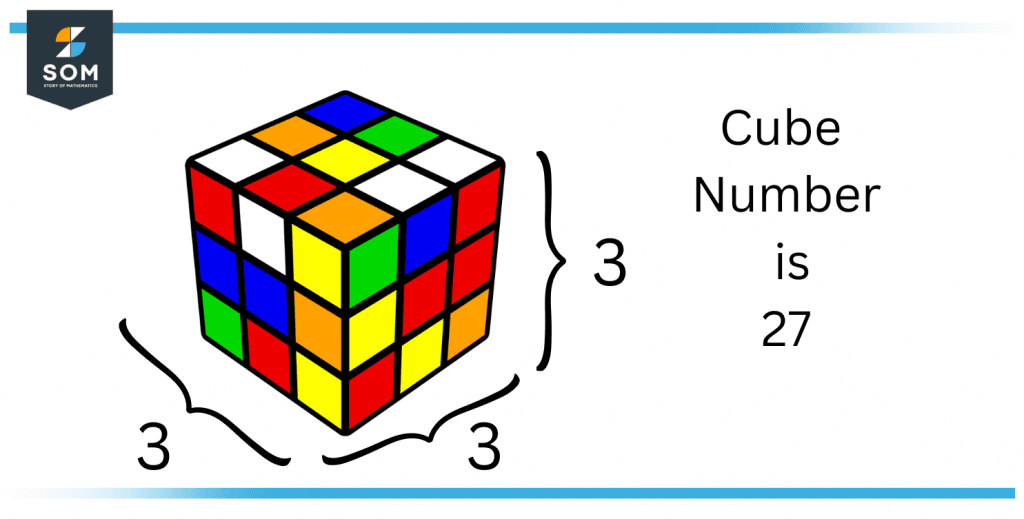
Figure 1: Concept of Cube
How To Find Cube Number
For example, $4 × 4 × 4 = 43 = 64$ i.e., this number is the exponential power of 3, or in other words, the result of multiplication by itself three times. For positive numbers, the cube number is also positive, while for a negative number, the cube number is also negative. This is because when a negative number is multiplied by itself number three times, it yields a negative number. For example, cube(-4) = – 4 × – 4 × – 4 = – 64 (i.e., three -ive signs multiplied by themselves yield a negative signed number). As we have seen, when -4 is multiplied three times, the result is – 64 i.e. a negative cube number. Following are a few more examples of cube numbers.
- – 3 × – 3 × – 3 = -33 = – 27
- 11 × 11 × 11 = 1331
- – 6 × – 6 × – 6 = -216
- 35 × 35 × 35 = 42875
In applications related to geometry, the volume of a cube = l × w × h, where l, w, h are the length, width, and height of the cube. As this calculation is done for a cube, therefore the length, width, and height are all equal lengths. Therefore, the volume of the cube is a$^3$ which reveals that the volume of the cube is also a cube number.
What Does Cubed Mean in Mathematics?
A cube number is a number that is the product of multiplying a number by itself and then by itself again. This is what we mean when we say that a value has been cubed. Cube numbers can also be represented in a visual way as diagrams of cubes, where the width, depth, and length each represent the number that is cubed. The representation of cube has been depicted in Figure 2 below.
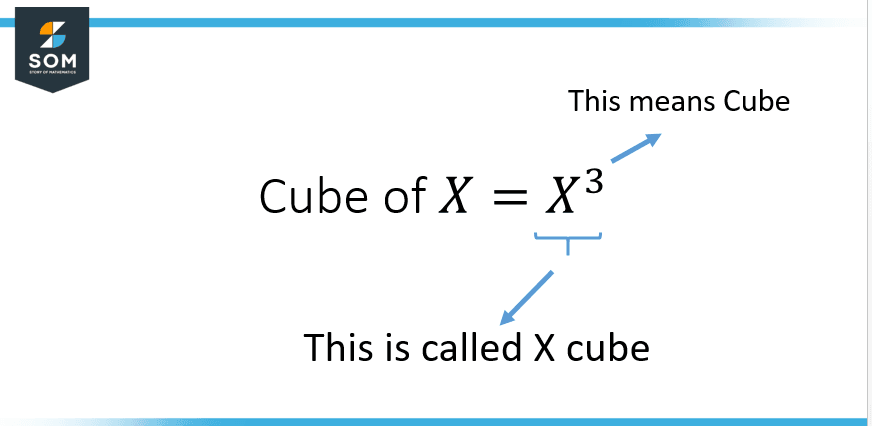
Figure 2: Symbol of Cube Number
How Are Cube Numbers Different From Square Numbers?
A square number is a number multiplied by itself once, whereas a cube number is one multiplied by itself before the process is repeated once more. This might sound a little complicated, but don’t worry, it’s really quite simple. Let’s take a look in more detail.
When we multiply 5 by itself, we get 25. So, the square of 5 is 25. Finding the cube of 5 involves just one extra step. Once we’ve worked out the square, we just need to multiply it by the original number again. In this case, the cube of 5 is 25 × 5 = 125. This can also be expressed as 5$^3$ = 125.
Cube Numbers in Real-life
While cube numbers are great for helping learners to understand number relationships and patterns, they have real-life applications too. For example, if we want to know the volume of a cubic object, such as a container, then we just need to cube the value of one of its sides.
By contrast, if a painter needs to know large the surface is of an object and knows the volume of an object already, they can work backward and find the cube root. By doing this, they’ll know how much paint they need. The information cube number tells in real-life problems is demonstrated in Figure 3 below:

Figure 3: Information obtained from a cube number
Perfect Cube Number
When we talk about a ‘perfect’ cube number, all we mean is a cube number that’s been created by multiplying a whole number, or integer, twice. All of the most common cube numbers that children learn at KS2 will be ‘perfect’. Here are the first four perfect cube numbers:
- 2 × 2 × 2 = 8
- 3 × 3 × 3 = 27
- 4 × 4 × 4 = 64
- 5 × 5 × 5 = 125
How Do You Cube a Number?
In arithmetic, the cube of a number is its third power. To cube a number, the number is multiplied by itself thrice = n × n × n. This can also be written like n$^3$.
Cube Numbers Facts
Following are some important facts about cube numbers:
- The last digit of the cube number will be the same as the number itself except for 2 which will change to 8 and 8 will get changed to 2 and 3 will be changed to 7, and 7 will be changed to 3. For example, cube number of 2 is 8 and of 3 is 27. In a similar way, cube 8 is 512, and cube of 7 is 343, and so on. Other than these numbers, the last digit of the cube number will be the same as the number itself e.g. the cube of number 6 is 216, a cube 9 is 729, a cube of number 11 is 1331, and so on. Note that the last digits of a resulting number and the number whose cube is taken are the same.
- The result for an even number cube will be an even number. For example 43 = 64 and so on.
- The result for an odd number cube will be an odd number. For example, 73 = 343, 93 = 729.
- The cube numbers can be either positive or negative. For example, both 64 and – 64 are cubes of 4 and – 4.
- The cube numbers can be written in terms of two, three, or more consecutive odd numbers e.g., 8 is a cube of 2 can be written as 3 + 5 = 8; whereas 27 can be expressed as a sum of 7 + 9 + 11 = 27.
Solved Examples
Example 1
Find the perfect cube of 19.
Solution
As discussed above, in order to find the cube number of 19 we multiply 19 by itself 3 times, that is, 19 × 19 × 19 = 6859 i.e., the required perfect cube number of 19 is 6859. Alternatively, we may write:
193 = 6859 or 19 × 19 × 19 = 6859.
Example 2
Compute the cube numbers for 9 and 11, and later, find the sum of the resulting cube numbers.
Solution
The perfect cube number of 9 is (9 × 9 × 9 = 729), and the perfect cube number of 11 is 1331 (11 × 11 × 11 = 1331).
Finally, the sum of the resulting cube numbers is = 729 + 1331 = 2060.
All images/mathematical drawings were created with GeoGebra.
