Cube Root|Definition & Meaning

Introduction To Cube Root 

The word root means the source, so by the literal definition, cube root means the cube of any number must be taken to get the original number. The product of a number multiplied thrice (three times) by itself is the cube of that specific number. A cube root is the inverse of the cube of any number, so if we take the cube root of a number, then the answer will always be the original number.

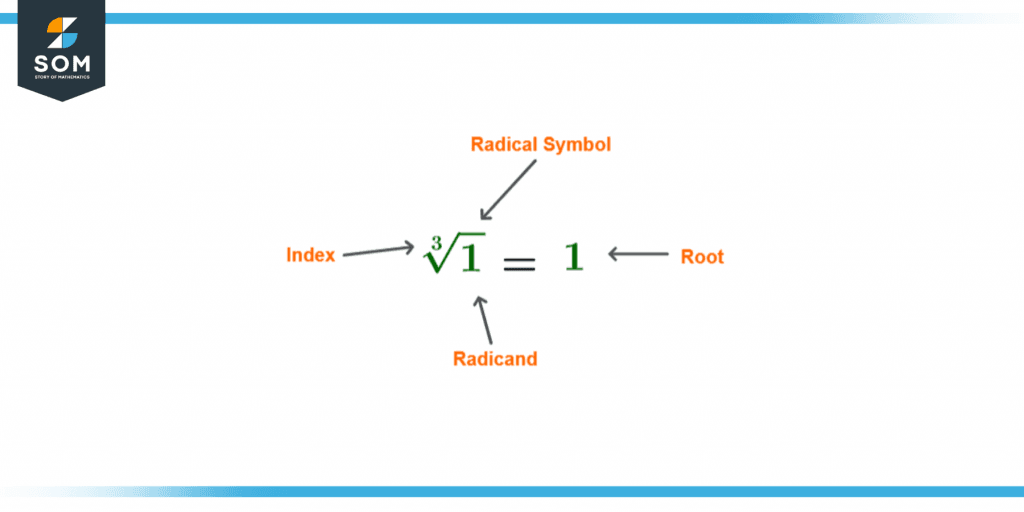
Figure 1 – Cube Root of 1

We represent the Cube root of any number by the radical symbol ‘$\sqrt{\phantom{a}}$ ’ with the 3 representing the cube. So the symbol of the cube root is ‘$\mathsf{\sqrt[3]{\phantom{a}}}$ .’ 

Let us take a number 2 to understand the concepts of cube roots. We know that when this number is multiplied three times, we get 8 as 2 × 2 × 2 = 8. So the number 8 is the cube of 2, which can be written as:

2³ = 8

Now to take the cube root of this number, we will use the inverse method. As discussed above cube root is a factor of the number itself:

$\mathsf{\sqrt[3]{8}}$ = 2

The cube root of 8 is, therefore, 2.

To solve the mathematical questions, we use the cube root formula to ease us. We can do this by finding the prime factorization of the number. After that, we take the cube root to the answer. Let us take the example of 64:

64 = 4 × 4 × 4

Now applying the cube root formula:

$\mathsf{\sqrt[3]{64}}$ = $\mathsf{\sqrt[3]{4\times4\times4}}$ = 4

Thus, 4 is the cube root of 64.

Perfect Cube

When we multiply 3 same integers with each other then the resulting cube is known as the perfect cube and similarly, the square root will be a whole number integer. Such numbers are known as cube numbers. 

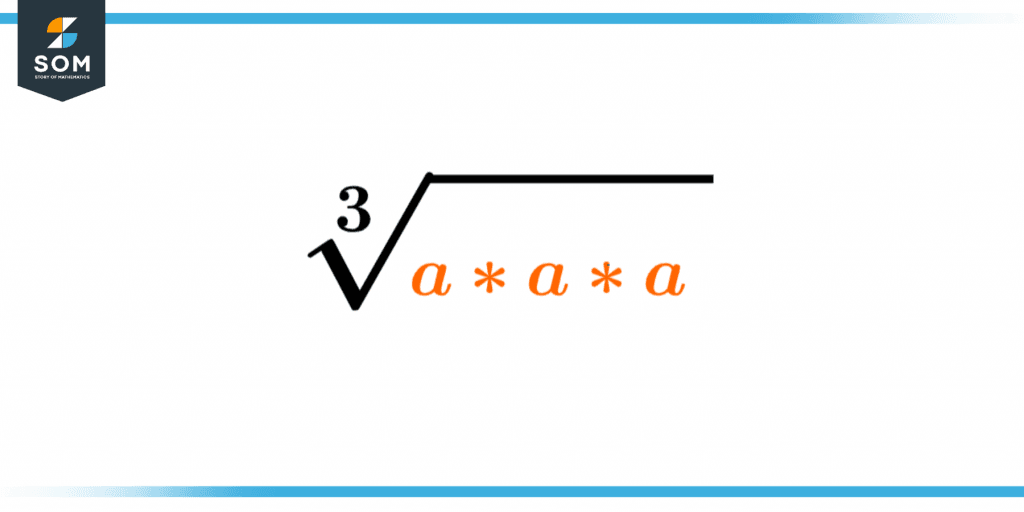
Figure 2 – Perfect Cube of A

Let us take the example of the number 27:

33 = 3 × 3 × 3 = 27

Now taking the cube root:

$\mathsf{\sqrt[3]{27}}$ = 3

Hence 27 is a perfect cube.

Not every number is a perfect cube if we take the example of the number 34 then we get:

$\mathsf{\sqrt[3]{34}}$ = 3.239

This is because it does not satisfy the condition in which the cube root must be a whole number integer.

Cube Root of Negative Number

The steps to find a negative number’s cube root are quite similar to the normal cube root. The following steps will be followed:

Let us consider a number x which is a negative number so to take its cube root we will rewrite it again while separating the negative sign from it:

Cube root of x = $\mathsf{\sqrt[3]{-x }}$

Cube root of x = $\mathsf{\sqrt[3]{(x(-1)}}$

Cube root of x = $\mathsf{\sqrt[3]{x } \left(\sqrt[3]{-1 }\right)}$

After separating the negative sign we do prime factorization on x and list all possible factors. We will then make groups of three and multiply them together so that we can get the cube root of x.

For -1 we will also calculate its cube root by following the same method and will multiply it by the cube root of x.

Note that the cube root of a negative number will always be a negative number and similarly the cube root of a positive number is also positive.

Properties of Cube Root

• The cube root of any odd number always give an odd number in the answer and similarly the cube root of all positive number will give a positive number.
• The cube root of all negative numbers is always a negative number.
• Any two imaginary cube roots, when multiplied will always give 1 as an answer.
• Cube roots are used to provide precise dimensions.

Examples of Cube Root

Example 1

Hailey is a part of a gaming club where you have to collect badges to level up. The highest record in this club is 216 badges. Find the number of Hailey’s badge if her level is the cube root of the highest record holder. Then tell how many more badges she needs to earn to become the record holder.

Solution

From the statement given above, we can say that the highest record is 216 so:

$\mathsf{\sqrt[3]{216}}$ = 6

So this tells that Hailey is on level 6 at the moment and to beat the record she needs:

216 – 6 = 210

210 badges are required for Hailey to reach the record but to break it she needs 1 more badge:

210 + 1 = 211 badges

Example 2

Todd wants to find the cube root of 2,744 for his math assignment. Help him find it.

Solution

We will solve this by using the prime factorization method so:

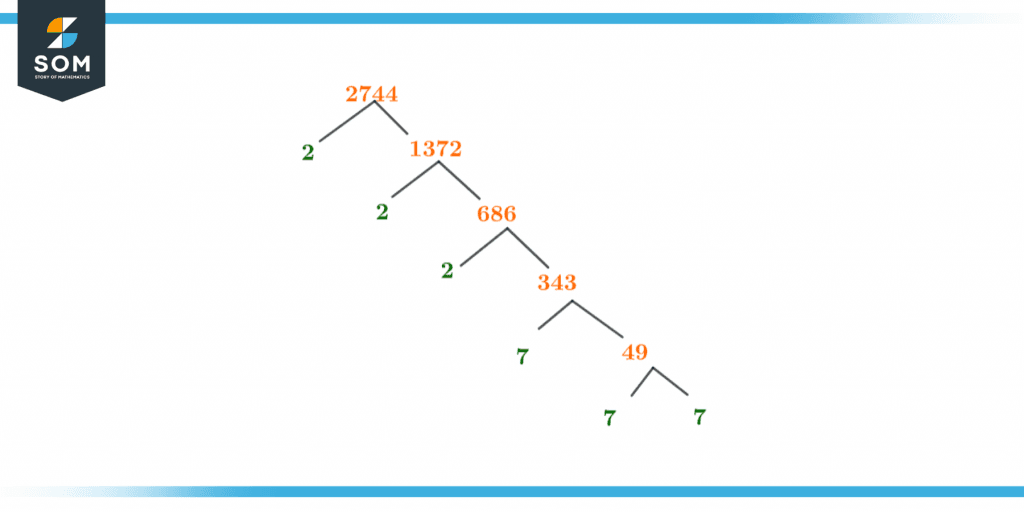
Figure 3 – Factor Tree Representing Prime Factorization of 2744

2744 = 2 × 2 × 2 × 7 × 7 × 7

Now we will group them so that we have 3 numbers in each pair:

2744 = (2 × 2 × 2) × (7 × 7 × 7)

2744 = 2³ × 7³

Now taking the cube root:

\[ \mathsf{\sqrt[3]{2^{3} \times 7^{3}} = \sqrt[3]{2^{3}} \times \sqrt[3]{7^{3}}} \]

= 2 × 7

= 14

So the Cube root of 2744 is the number 14.

Example 3

Solve and check whether the following numbers are perfect cubes or not

a) 512

b) 48

Solution 

a) 512

First, we use the prime factorization method:

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

Now we will group them together:

512 = (2 ×2 × 2) × (2 × 2 × 2) × (2 × 2 × 2)

512 = 2³ × 2³ × 2³

Now taking the cube root:

\[\mathsf{\sqrt[3]{ 512 } = \sqrt[3]{ 2^3 × 2^3 × 2^3}} \]

$\mathsf{\sqrt[3]{ 512 }}$ = 8

Hence 512 is a Perfect Cube.

b) 48

First, we use the prime factorization method:

48 = 2 × 2 × 2 × 2 × 3

Now we will group them together:

48 = (2 × 2 × 2) × (2) × (3)

48 = 2³ × 2 × 3

Now taking the cube root:

\[ \mathsf{\sqrt[3]{ 48 } = \sqrt[3]{ 2^3 × 2 × 3}} \]

\[ \mathsf{\sqrt[3]{ 48} = 2\sqrt[3]{ 6}} \]

$\mathsf{\sqrt[3]{48}}$ = 3.63

Hence 48 is not a Perfect Cube.

Images/mathematical drawings are created with GeoGebra.

Cube Number Definition < Glossary Index > Cubic Centimeter Definition