Cubic Meter|Definition & Meaning

What Is a Cubic Meter? 

A cubic meter or also known as meter cube meter³, is a unit described by the international systems of units. A meter cube is used for defining the volume of a 3-dimensional object. The object has to be 1 meter long, 1 meter wide, and 1 meter tall for the cubic meter to be accurate.

A cubic meter is also equivalent to 1000 liters, which means that you can put 1000 liters of water inside a cube of 1-meter measurement on all sides. The symbol to represent a meter cube is m³.

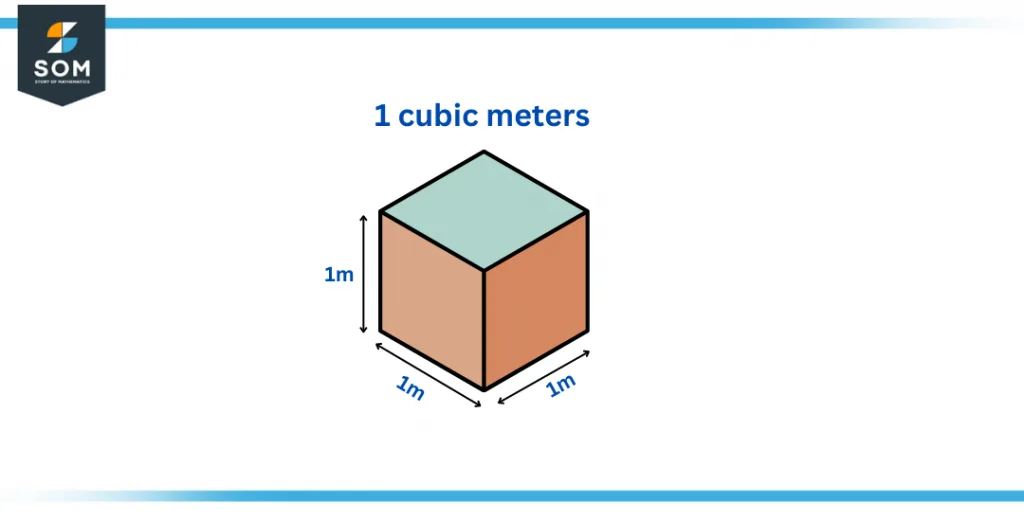
Figure 1 – One cubic meter as the volume of a cube

It is called a cubic meter because all the sides of a cube have equal length, and if one side is of 1-meter then the volume of a cube becomes,

Volume = length x breadth x width

Since,

 length = breadth = width = 1 m

Volume = V = 1m x 1m x 1m

V = 1m³ or 1-meter cube

The edge-to-edge distance of a cube must be 1 meter in length so that the volume can be calculated as 1 cubic meter. Another name that is used rarely in mathematical or physical literature is kiloliter, as 1000 is equal to a kilo.

Suppose you are building a sand castle, and you are interested in knowing how much sand you carry at every bucket full. For this, you need to know the volume of the bucket you are filling.

Cubic meters help determine the volume of any solid or liquid inside an object, like a bucket. To measure the exact volume of sand, fill the bucket until it is fully equipped with sand. Similarly, measuring the volumes of other objects, like the amount of space inside a deep refrigerator, the amount of soil required to suffice up a gardening bed, or the amount of water required to fill up a mini pool.

Visualizing a cubic meter is a bit hard task to perform, but it can be said that a person could fill up a container of 1 cubic meter volume with 260 gallons of milk.

What Is Volume?

The phrase volume can have different meanings depending on the type of application, it can be the volume of music on the radio or the ones we use in geometrical applications, but in mathematics, volume is the total space occupied by a 3-dimensional object in a given space.

Since it covers up space in 3-dimensional geometry, its units are measured in sets of cubes such as cubic meters, cubic inches, etc.

Explanation In Real Life

The concept of volume is used in everyday problems, from measuring the milk you buy from the store to filling up your backyard with gardening soil. Understanding the notion of volume will be especially crucial for any individual who plans to purchase compost for their lawn in the future.

Instead of being offered by mass, compost is frequently sold by volume. Some retailers sell sacks with cubic foot measurements. Massive amounts are offered mostly in cubic yards by some providers. It’s crucial to understand that one cubic yard contains 27 cubic feet while examining costs.

Water tables in the open sea are increasing by a decade due to human–caused climate change. However, predicting how large and how quickly they would grow is crucial for researchers.

Researchers can predict rising sea levels by estimating the volume of glaciers contained inside icecaps, such as those in Antarctica and Greenland. The encouraging stuff, as of 2022, is changing gradually, at a pace of around 1 inch per ten years. Is it devastating news? Around the year 2100, water levels would likely be 1.5–3, surpassing due to the acceleration of climate change.

Calculating Cubic Meter Volume

A cubic meter is an SI unit for calculating the volume of a 3-dimensional solid. A cubic meter is used to calculate the volume of liquid and solids, but since liquids are difficult to contain, the end result is just the volume of the solid they are collected in.

So for all types of 3-dimensional objects, the volume is calculated in cubic meters or sometimes in cubic centimeters, which all depends on the unit being used for the dimensions of the object in that circumstance.

For instance, we have a cube whose edges are 3m in length each; thus, the volume of the cube will be:

Volume = length x width x height

Or,

Volume = Edge x Edge x Edge

Since we have the edge distance and all the edges are of the same length, we will use the second formula:

V = Edge³

V = 3³

V = 9 m³

Now let’s say we have a cuboid with different side lengths of 2cm, 4cm, and 6cm, and we are required to find the volume of this cuboid. Using the first formula we wrote:

Volume = length x width x height

V = 2cm x 4cm x 6cm

V = 48 cm³

Cubic Meter Conversion

Sometimes the cubic meter can be a huge value, so to narrow it down or reduce the size of it, we have to convert it into a relatable unit that is used widely, such as cubic centimeters, cubic millimeters, and so on. We will be discussing a few conversions of cubic meters to other sets of units.

Cubic Meter To Cubic Centimeters

One cubic meter is a huge quantity when comparing it to cubic centimeters; since one meter is equal to 100 centimeters, one cubic meter is 100³ cubic centimeters or 1000000 cm³.

How Is It Done?

Since we know that one meter is equivalent to 100 centimeters. If we take a cube on both sides, it will result in cubic units. Thus,

1 cubic meter = 100 x 100 x 100 cubic centimeters

1 m³ = 100³ cm³

1 m³ = 1000000 cm³

Cubic Meter To Simple Meter

The formula to calculate cubic meters is as follows:

Cubic meter  = meter x meter x meter

Thus if we divide the volume by any two sides, we can get the conversion from cubic meter to meter.

The following conversion table will help you understand better.

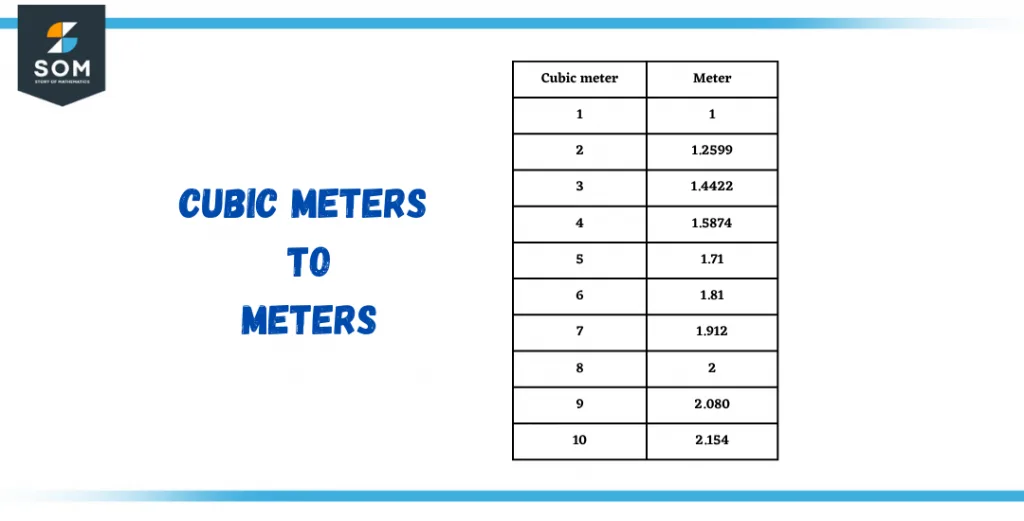
Figure 2 – Conversion of cubic meters to meters

Cubic Meter to Meter Square

When we are calculating the area of an object, we make use of a meter square as the unit, whereas meter cube is used as the unit for the volume of a 3-D object.

When finding the area, we make use of the length and width only, whereas, in volume, three sides come into play, length, width, and height. Thus the conversion of a meter cube to a meter square can be carried out by dividing the meter cube by the width of the object.

We should know that a one-meter cube is precisely equal to a one-meter square.

The below table will demonstrate the other conversions.

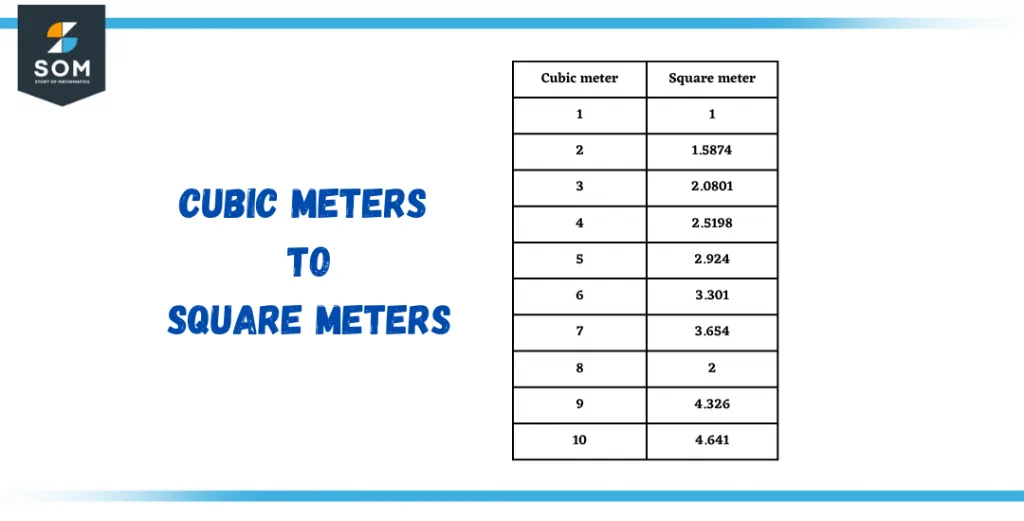
Figure 3 – Conversion of cubic meters to square meters

Cubic m to Cubic ft

One meter contains roughly about 3 feet of distance, precisely:

One meter = 3.280 feet.

So for cubic meters, we can multiply this 3 times to get the desired conversion:

One cubic meter = 1 meter x 1 meter x 1 meter

1 m³ =  3.280 ft x 3.280 ft x 3.280 ft

1 m³ = 35.31466 ft³

Similarly, some other conversions are given below:

1 m³ = 35.31 ft³

2 m³ = 70.63 ft³

3 m³ = 105.94 ft³

4 m³ = 141.26 ft³

5 m³ = 176.57 ft³

Example of Converting Cubic Feet To Cubic Meters

Convert 0.08 Cubic Feet to Cubic Meters?

Solution

Since we know:

1 cubic meter  = 3.280 feet

1 cubic feet  = 0.0283 meters

Therefore:

0.08 ft³ = 0.08 x 0.0283 m³

0.08 ft³ = 0.002265 m³

So, 0.08 cubic feet is equal roughly to 0.002265 cubic meters.

All images are created using GeoGebra.

Cubic Centimeter Definition < Glossary Index > Cylinder Definition