Cylinder|Definition & Meaning

What Is a Cylinder? 

A cylinder is a solid geometrical shape that comprises two flat and circular bodies at the ends, bounded by a curved surface at a particular distance. A cylinder is a geometrical figure in a 3-dimensional plane. The circular faces are the base of the cylinder, and the space or length between these two bases is called the height.

The bases are identical and parallel to each other. The center line merging the circular bases is the axis of the cylinder. The height is the perpendicular stretch between the bases. As the bases are circles, the curved surface is like a rectangle; hence the cylinder is a combined figure including circles and rectangles.

Unlike some other 3D shapes, the number of vertices of a cylinder is zero. An object holding a shape like a cylinder is said to be cylindrical. Many daily life objects are cylindrical in shape, for example, wood logs, cells, cold drink cans, pipes, fire extinguishers, and many more.

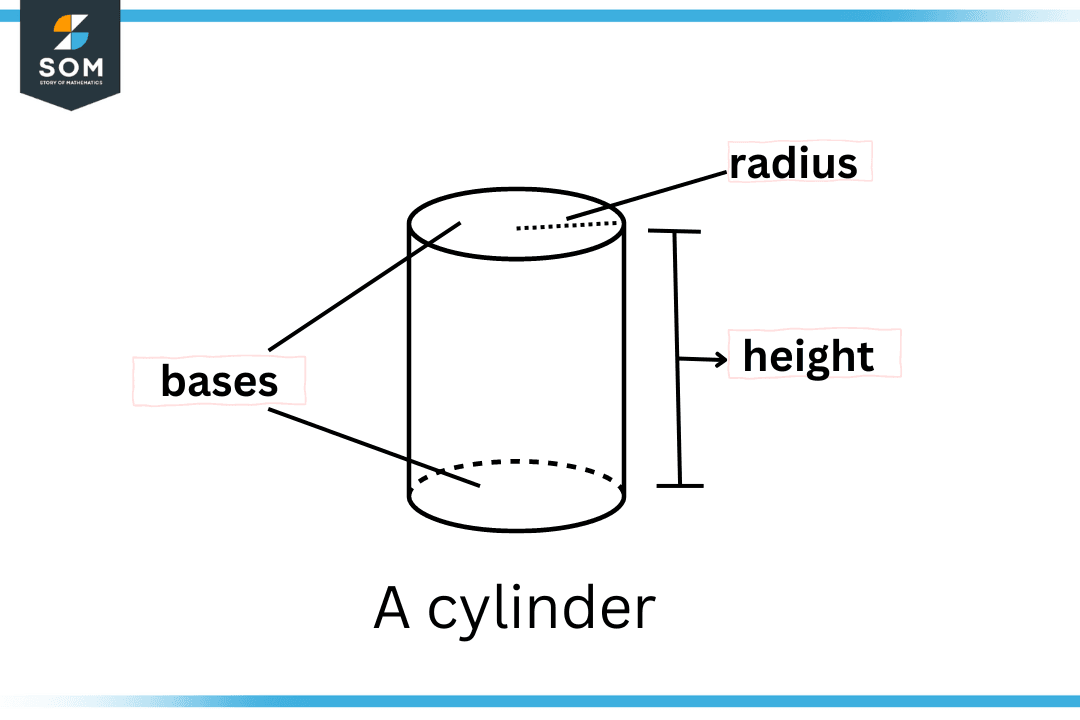
Figure 1 – A common geometrical cylinder

Properties of Cylinder 

The most basic properties of a cylinder are as follows:

• It may consist of two flat circular or elliptical bases.
• Its curved surface joins the bases of the cylinder.
• The bases of a cylinder are invariably parallel and congruent to each other.
• It has 2 two curved edges but no vertices.
• The distance of the bases from the center point to the exterior boundary is the radius of the cylinder. 
• The size of the cylinder is determined by the radius and height.
• Curved surface area, total surface area, and volume of a cylinder can be estimated using radius and height.
• Right Circular cylinders, oblique cylinders, and elliptical cylinders are some of the kinds of cylinders.
• A cylinder has two kinds of surface areas, i.e., lateral surface area and total surface area.

The Volume of a Cylinder 

It is the portion of space occupied by the cylinder in a 3-dimensional plane. The volume tells us how much of the quantity can be stored in the cylinder. It can be determined by multiplying the area of the base, i.e., πr², and height, i.e., h.

Cylindrical Volume = πr²h

Lateral Surface Area of a Cylinder

The portion of a cylinder that is slightly curved around the edges of the rounded area is represented as the lateral surface. It is the amount of space bounded between the borders of the curved area of the cylinder. Lateral surface area is also going by the name curved surface area. Using the formula given below, we can easily figure out the lateral area:

Cylindrical lateral area = 2πrh square units

Where r represents the radius and h stands for the height of the cylinder.

The Total Surface Area of the Cylinder

As the name indicates, it is the area shielded by the cylinder as a whole. It includes the area of the bases as well as the area of the curved part of the cylinder. The total surface area is evaluated by the addition of the lateral surface area and the area of the bases.

Area of circular base = πr² 

Cylindrical lateral area = 2πrh square units 

Since a cylinder has two circular bases, therefore we multiply the area of the circular base by 2.

Total area of surface = lateral area + 2(area of circular base) = 2πrh + 2(πr²)

Absolute cylindrical surface area = 2πr(h + r) square units

The Radius of the Cylinder

The Radius of the cylinder is determined by finding the radius of its bases. It is the length from its center point to the outer boundary. Radius is generally denoted by r. It is usually measured in cm,m, mm, and ft. The formula for finding the radius can be evaluated using the formula for the volume of a cylinder:

The volume of the cylinder = V = πr²h cubic units

r² = V\πh

r = √V\πh

Where r denotes the radius, V is the volume, and h is the height of the cylinder.

The Height of the Cylinder

The height is the measure of the length between the two bases of the cylinder. The notation used for height is h. The height is usually measured in m, cm, mm, and ft. The formula of height can also be determined by utilizing the equation provided below for the cylindrical volume:

The volume of the cylinder = V = πr²h cubic units

H = V \ πr²  

Where h denotes the height, V is the volume of the cylinder, and r stands for the radius of the cylinder.

Circumference of Cylinder

Since a cylinder includes circular bases, it also constitutes some circumference. The circumference of the cylinder is basically the measure of the length of the boundary of the circle. The circumference is measured in the same units as lengths. To estimate the circumference of a cylinder, we have the following formula:

Circumference of cylinder =  2πr 

Types of Cylinders

In geometry, there are four classifications of cylinders. Namely

• Right circular cylinder
• Oblique cylinder
• Elliptical cylinder
• Right circular hollow cylinder 

Let us discuss the differences and descriptions of these cylinders.

Right Circular Cylinder

A cylinder whose axis is at a 90-degree angle or perpendicular to the bases is known as a right cylinder. When the bases are circular in shape, it is named a right circular cylinder.

The volume of the right circular cylinder = πr²h cubic units

Right circular cylinder surface area= 2πrh + 2πr² square units

Right circular cylinder lateral area= 2πrh  square units

Oblique Cylinder

It is opposite to the right circular cylinder. The Oblique cylinder has no perpendicular axis; hence its sides incline over the base. Both bases are not directly in front of each other. It is a tilted or inclined form of a circular cylinder. The famous leaning tower of Pisa is an oblique cylinder.

The volume of the oblique cylinder = πr²h cubic units

Total Surface area of the oblique cylinder = h + 2πr²  square units

Lateral surface area of the oblique cylinder = 2πrh  square units

Elliptical Cylinder 

A cylinder whose bases are in the shape of an ellipse is known as an elliptical cylinder. Or we can also define it as a cylinder whose cross-section is an ellipse in shape.

The volume of the elliptical cylinder = πabL cubic units

Where a denotes the semimajor axis, b denotes the semiminor axis, and L is the length of the cylinder.

The lateral surface area of the elliptical cylinder = perimeter * height

Base area of the elliptical cylinder = abπ square units

Total surface area = 2A + L square units

Where A is the base area, and L is the lateral surface area.

Right Circular Hollow Cylinder

It is a cylinder that comprises two cylinders in such a manner that one is bordered by the other. Both cylinders are right circular cylinders. This cylinder has one point of the axis, and it is also perpendicular to the center of the base.

The term hollow in the name of this cylinder is due to the reason that the inner part of the cylinder is hollow, unlike the right circular cylinder. The right circular hollow cylinder has another name, i.e., cylindrical shell.

The volume of the right circular hollow cylinder = π(R² – r²)h cubic units

Lateral surface area = 2πrh square units

Base surface area = πr² square units

Total surface area of the right circular hollow cylinder = (2πrh + 2πr²) square units

= 2πr(h + r) square units 

Net of a Cylinder 

A geometric net, also referred to simply as a net, is a two-dimensional representation of a three-dimensional geometric shape. It displays what the figure would look like if its sides were flattened and all its faces were visible. In other words, it’s a pattern of a solid figure that can be folded into a 3D shape.

Three-dimensional figures can be made by folding nets. Unfolding a cylinder portrays two circles attached to either side of the rectangle. The circles symbolize the top and bottom circular bases of the cylinder, and the rectangle represents the curved part of the cylinder.

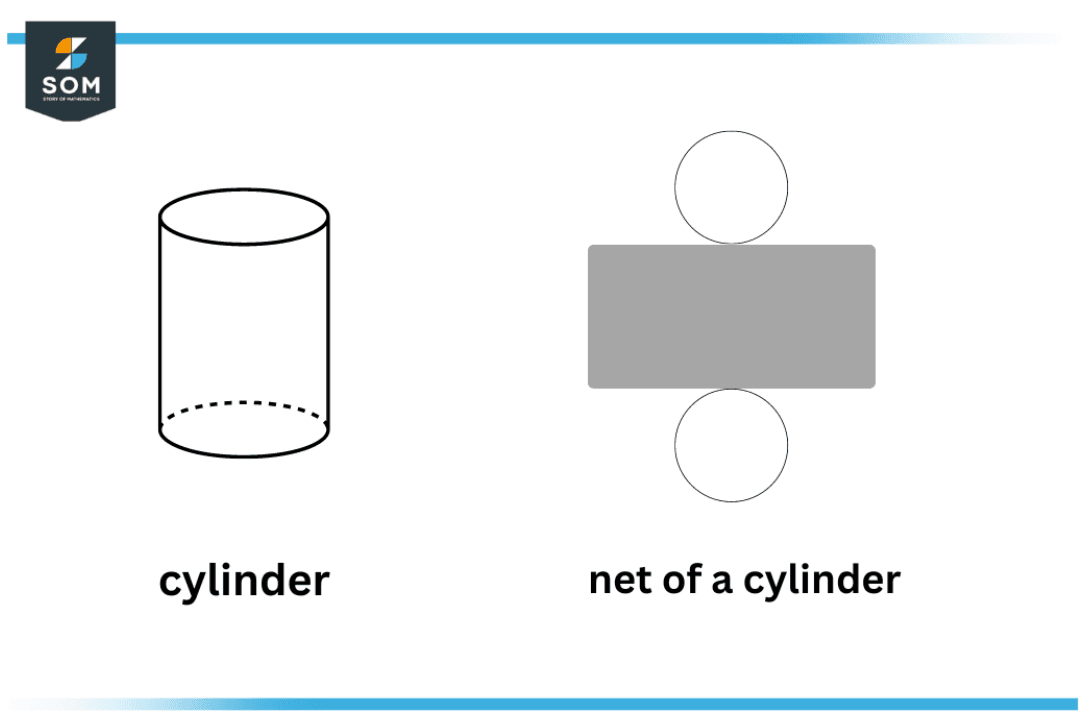
Figure 2 – Net of a cylinder

Other 3D Shapes

As a cylinder is a 3-dimensional figure, there are many other 3-dimensional shapes used in geometry, named as:

• • Cube
  • Cuboid

• Pyramid

• • Cone
  • Sphere

• Tetrahedron

All the 3-dimensional geometric figures have specific volumes and surface areas according to their geometric structures. They have a number of vertices, edges, and faces.

For example, a cube consists of 6 facades and has a total of 12 edges, and 8 symmetrical vertices, whereas a sphere has 1 curved face, zero edges, and zero vertices. The net of all the 3-dimensional shapes can also be formed. 

Cylindrical Objects 

Any object constituting a cylinder-like shape is said to be cylindrical. There are many cylindrical objects we see and use in our daily routine. The pencil holder we use for holding our pens and pencils is basically a cylinder. The LPG gas cylinder is cylindrical in shape.

The food cans or cold drink cans which we enjoy eating and drinking are examples of cylinders. Buckets and dustbins are also cylindrical in shape. The trunk and log of wood are also in the form of a cylinder. Candles, chimneys, drums, beakers, and test tubes are also examples of objects in a cylindrical shape.

Figure 3 – Some common examples of cylindrical shapes used in daily life

Practical Application of Geometrical Cylinders

Cylinders have a wide range of practical applications in engineering and technology, making them an important shape in the field. The most common uses for cylindrical shapes can be demonstrated as follows:

1. Containers: Cylinders are often used as containers for various products, such as liquids or solids. This is because they offer efficient use of space and can withstand stacking and pressure.
2. Pipes: Cylinders are also used in piping systems to transport liquids and gases, as they have a large interior volume and a small exterior surface area.
3. Engine Design: Cylinders play a key role in internal combustion engines. They are used to contain the fuel and air mixture, which is compressed and ignited to produce power.
4. Pressure Vessels: Cylinders are used as pressure vessels for storing compressed gases, boilers, and heat exchangers. They provide a strong and efficient structure to withstand high pressures.
5. Bearings: Cylinders are used as rollers and bearings in conveyor rollers, wheels, and gears. The smooth cylindrical surface offers low friction and wear resistance, making them ideal for high-speed and high-load applications.
6. Electrical Equipment: Cylinders are also utilized in electrical equipment such as transformers, inductors, and capacitors. They help control electromagnetic fields.
7. Medical Devices: Cylinders are used in medical devices such as syringes, catheters, and IV bags. The cylindrical shape is convenient and easy to use for administering fluids to patients.

Only a handful of numerous practical applications of cylindrical shapes were provided in the above topic in engineering and technology. Their versatility, combined with their strength and efficiency, make them an essential element in many products and systems. 

Solved Examples Involving Cylinders

Example 1

A cylindrical bucket with a height of 30cm and a 15cm wide base radius is filled with sand. What will be the total surface area and volume of the bucket?

Solution

Given data:

Height = h = 30cm

Base radius = r = 15 cm

Total surface area = A = ?

Volume = V = ?

First, we find the total surface area using the formula:

Cylindrical surface area = 2πr(h + r) square units

Putting the values of radius and height in the above formula:

A = 2 * 3.141 * 15(30 + 15)

   = 2 * 3.141 * 15(45)

   = 2 * 3.141 * 675

   = 1350 * 3.141

   = 4240 cm²

Finding the volume of the bucket by using the formula:

Volume of cylindrical bucket= πhr²

Putting the values of radius and height in the above formula:

V = 3.141 * 30 * (15)² 

V = 20.925 cm³.

Hence, the cylindrical bucket has a total surface area of 4240 cm² and a volume of 20.925 cm³.

Example 2

What will be the radius of the cylinder whose volume is 550 cm³ and height of 5cm? 

Solution 

Given data:

Height = h = 5cm

Volume = V = 550 cm³

Radius = r = ?

Using the formula of volume, we can find the radius as:

Volume = V = πhr² cubic units

r² = V \ πh

r = √V \ πh

Putting the values of volume and height in the above formula:

r = √550 \ (3.141*5)

r = √550 \ 15.705

r = 6 cm

Hence, a cylinder with a volume of 550 cm³ and a height of 5 cm has a radius of 6 cm. 

All images were created with GeoGebra.

Cubic Meter Definition < Glossary Index > Data Definition