Decompose|Definition & Meaning

Why Is Decomposing Important? 

It is essential to decompose the numbers to develop a clear concept of mathematics and geometry. Decomposition can either be of shapes or numbers. By decomposing the shape, we can get the parameters of the shape, while on the other hand, by decomposing the numbers, we can get a clear sense of numbers and their relations with the digits.

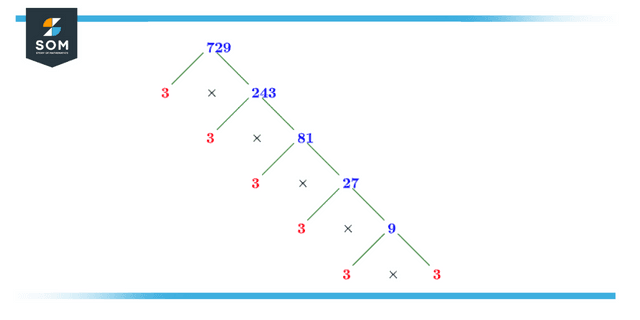
Figure 1: Illustration of decomposition by prime factorization

Composing vs. Decomposing

Compose is the exact opposite of decompose. As decomposing means breaking numbers into their parts, composing in math means writing numbers together. In simple words, the numbers taken apart to write them together are called compose. For example:

• Compose 7 hundreds, 8 tens and, 2 ones.

It is written as 700+80+2, which equals 782.

• Compose 12 thousands, 3 hundreds, 7 tens, and 3 ones.

It is written as 12000+300+70+3, which is equal to 12373.

• Compose 5 hundreds and 5 tens.

It is written as 500+50 and equals 550.

How Do Shapes Decompose?

The decomposition of shape is to break the shape into other smaller shapes. The newly formed shape can be wholly different or the same in a smaller size.

Let’s take an example of a square. We can break this square into several different types of shapes. We can break it into smaller squares, or we can break it into a triangular form, or it can be a combination of triangles and squares or what so ever.

Daily Life Examples

Some real-life examples of decomposing of shapes are as follows;

• If we cut a pizza, we break a circular shape into triangular shapes.
• If we cut A4 size paper into two halves, we break a rectangular shape into two smaller rectangles.
• If we cut a lemon into two halves, we break a circle into two semi-circles.

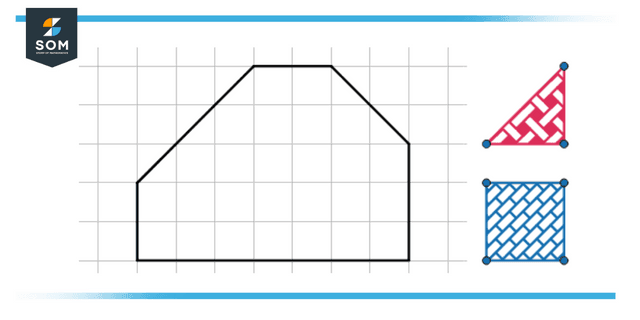
Figure 2: Illustration of decomposition of shapes.

It is an irregular shape which is decomposed into two different shapes, a triangle and a square. It can further be decomposed into a rectangle.

Process of Decomposing Shapes

There’s, as such, no rule for the decomposition of shapes. Consider an aeroplane. When you think of it, you will imagine only one figure. But when you think of it in shapes, different geometric shapes will definitely pop up in your mind. You can divide the figure into shapes like a trapezoid, rectangle, triangle and many others.

How To Decompose Numbers?

Decomposing numbers help us understand and comprehend patterns and relationship between large numbers or digits in an equation. Numbers are decomposed into thousands, hundreds, tens, and one’s places or are decomposed by breaking numbers into various addends.

Figure 3: Illustration of decomposition by the least common factor.

In this figure, 72 and 120 are being decomposed, and their least common factor is 360.

Methods To Decompose Numbers

There are a couple of methods to decompose numbers, as discussed below.

Method One: Decomposing Into Hundreds, Tens, and Ones

Firstly, we will figure out the concept of ones and tens if we have a two-digit number without any decimal place. Then the number on the left side is tens, and the number on the right is ones. After knowing which digit is at the tens place and which is at one’s place, break down the number into its parts. In others words, we can say numbers are taken apart.

A three-digit number with no decimal place, the number on the right side is ones, the number on the left-hand side is hundreds, and the number in the middle is tens. When we break the three-digit number, we will decompose it into three pieces: ones, tens and hundreds. The same principle is applied to large numbers and infinite numbers.

Now let us understand how decimals work. When we have digits on both sides of a decimal point, we must decompose them by breaking down numbers into parts on both sides.

• The tenth place is used by the single digit that comes right after the decimal point.
• The hundredth place is used when two digits are right after the decimal point.
• The thousandth place is used when there are three digits right after the decimal point.

The left side can be decomposed by the same method when there is no decimal point in the equation.

Method Two: Decomposing Into Various Addends

Decomposing addends means breaking the numbers into a different sets of numbers. If we subtract one addend from the actual number, the required answer should be the second ad, and when we add both, the actual number should be the sum we calculate.

Example 1

Decompose the number 561.58

Solution

• The hundreds place is 5, so it can be written as 500
• The tens place is 6, so it is written as
• 60
• The ones place is 1, so it is written as 1
• In tenths place, there is 5, so we can write it as: 0.5
• At hundredths place, there is 8, so we can write it as 0.08
• The final answer can be written as: 561.98 = 500 + 60 + 1 + 0.5 + 0.08

Example 2

Decompose the number 73

Solution

• At tens place, there is 7, which is separated and written as: 70
• In ones place there is 3, which is separated and written as 3
• The final answer that we get in the end is written as 73 = 70 + 3

Reminder: when a number is written in its standard form, it is called the standard form. But the form is expanded if written in its decomposed form.

According to the previous example that we have written, “73” is the standard form and “70 + 3” is the expanded form, as the numbers are shown in the decomposed way.

All images/graphs are created using GeoGabra.

Decimal Point Definition < Glossary Index > Decrease Definition