JUMP TO TOPIC
Decimal Point|Definition & Meaning
Definition
Decimal point, represented by “.“, is used to separate the whole part and the fractional point of a number. For example, in the number 23.75 the decimal point separates the whole part 23 from the fractional part of 75.
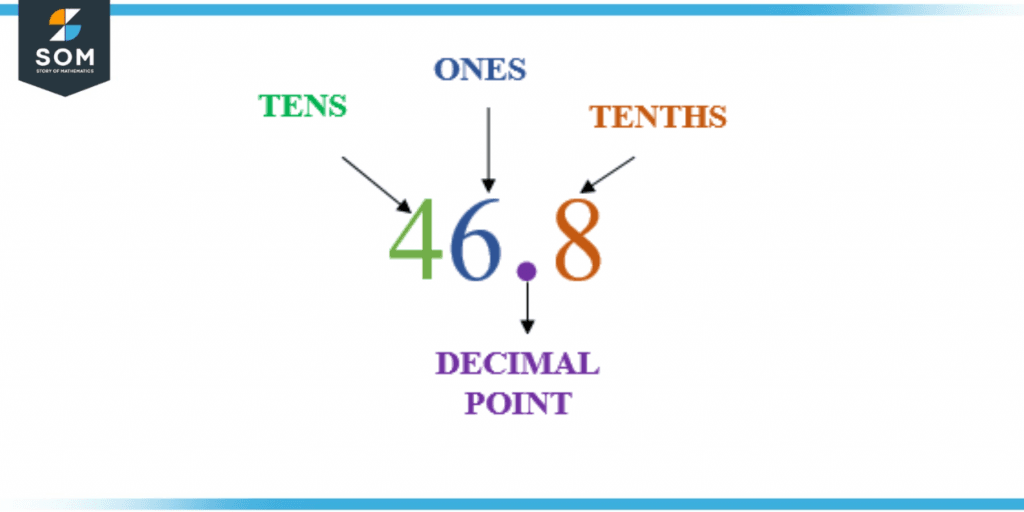
Figure 1 – Decimal Point
Here in the figure above decimal point is after 2 place values, and after it (to its right), there is only one place value.
Starting from the decimal points, the first place value or digit on the left side is the ones digit, followed by a tens, and further followed by hundreds, thousands, and so on. To the decimal point’s right, however, the first place value is tenths (1/10), the next is hundredths (1/100), then thousandths, and so on.
Concepts of Decimal
In mathematics, a decimal number is a symbol that represents the division of whole numbers into their component parts. In decimal notation, a value that isn’t a whole number is typically denoted by a period (.) or dot (.).
The decimal point indicates the order of the numbers in a decimal system. The numbers to the decimal point’s left represent the whole number, while the numbers to its right represent the fractional half. For instance, the number 3 represents the entire number (or integer) in the decimal number 3.11, whereas the digits to the right of the decimal “.11” indicate the fractional part.
Decimal numbers can also be expressed in scientific notation. In scientific notation, a decimal number is written as a number between 1 and 10, multiplied by a power of 10. For example, the decimal number 3.11 can be written as 3.11 x 10^0. In scientific notation, the decimal point is not used, but the exponent indicates the position of the decimal point.
Further Explanation
A combination of whole integers and fractional parts represents numbers in decimal notation. The decimal point is placed to the left of the fractional components and to the right of the integer components. In other words, it comes after the integer part and before the fractional part. For instance, the whole number in the numeric value 3.11 is 3, and the fraction part is 11.
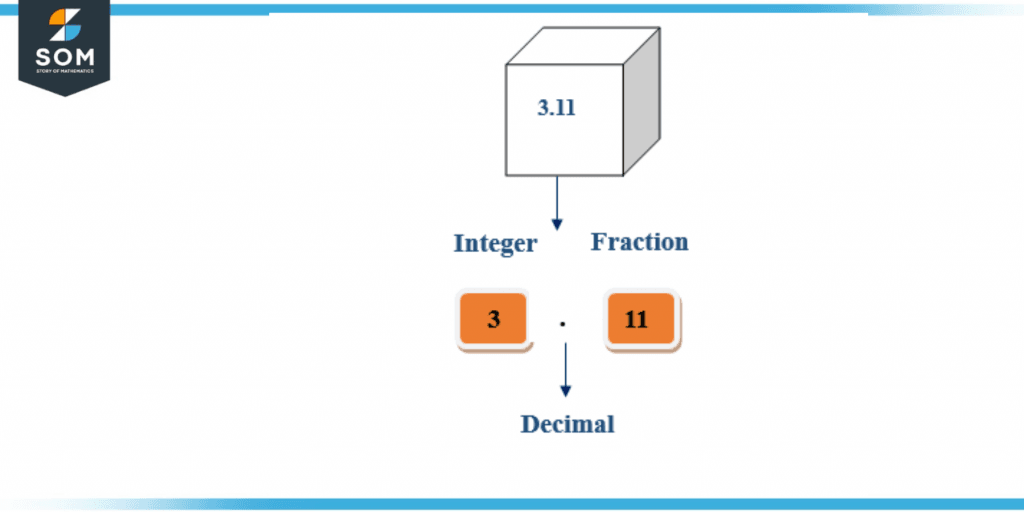
Figure 2 – Pictorial Presentation
Here in the figure above, the number represented is 3.11, where 1 is in the ones place, 1 is in the tens place, 3 is in the hundreds place, and the dot (.) between them represents a decimal point.
Decimals can also be used to represent ratios and proportions. For example, if a cake recipe dictates four and a quarter cups of flour, one and a half cups of sugar, and two and a quarter cups of milk, the proportion of flour to sugar to milk can be represented as 4.25 : 1.5 : 2.25 or 4.25/8 : 1.5/8 : 2.25/8.
By expressing these ratios as decimals, we can see that flour makes up 4.25/8 = 0.53125 or 53.125% of the recipe, sugar makes up 1.5/8 = 0.1875 or 18.75% of the recipe, and milk makes up the remaining 28.125% of the recipe.
Significance
Decimal points are also used in many financial transactions, such as calculating interest rates, currency exchange rates, and stock prices. For example, if a bank offers an interest rate of 3.5%, the decimal point indicates that the interest rate is not a whole number but rather a fractional part of a whole number.
Similarly, if a currency exchange rate is 1.23 dollars to 1 euro, the decimal point indicates that the exchange rate is not a whole number but a fractional part of a whole number.
Decimal points also play an important role in measurement and calculation. The decimal point is an important symbol in mathematics that is used to indicate the separation of whole numbers from fractional parts.
It is used in decimal notation to indicate a non-whole number and is also used in scientific notation, ratios and proportions, financial transactions, and measurement and calculation.
Understanding the decimal point is essential for understanding the meaning of decimal numbers.
Decimal Place and Decimal Point
A decimal place refers to the position of a digit in a number expressed in decimal notation. The decimal point separates the whole number part of a decimal number from its fractional part.
It’s important to understand the concept of decimal places and decimal points when working with decimal numbers, as it allows us to perform arithmetic operations like addition, subtraction, multiplication, and division and compare decimal numbers with precision. It also helps understand the concept of rounding decimal numbers down or up to a specified number of decimal places.
Decimal place refers to the position of a digit in a number expressed in decimal notation, while Decimal point is a symbol (.) used to separate the whole number part of a decimal number from its fractional part.
Understanding the concept of decimal places and decimal points is important in various fields, such as mathematics, engineering, and finance, as it allows us to perform arithmetic operations and compare decimal numbers with precision.
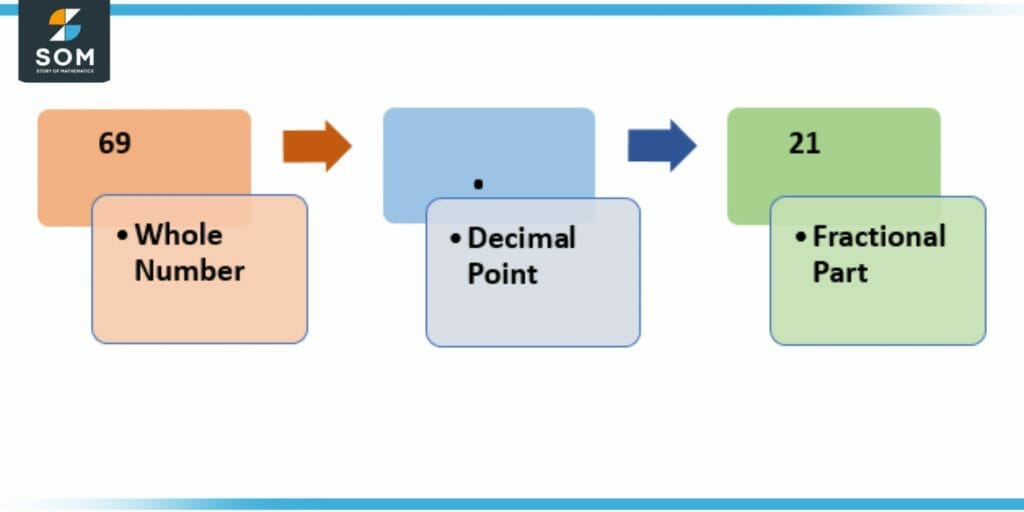
Figure 3 – Parts of Decimal Numbers
In this example, the number represented is 69.21, where the dot (.) represents the decimal point, the part to its left represents whole numbers, and the part to its right represents the fractional part.
A decimal place value chart is a visual representation of the place value system used in decimal numbers. It shows the relative position and value of each digit in a number, with the rightmost digit having a place value of ones, the next digit to the left having a place value of tens, the next digit to the left having a place value of hundreds, and so on.
Examples of Decimal Point and Its Usage
We’ll start with whole numbers and see how decimal points help make measurements more precise in these examples.
Example 1
Identify the place values in the whole number 3478.
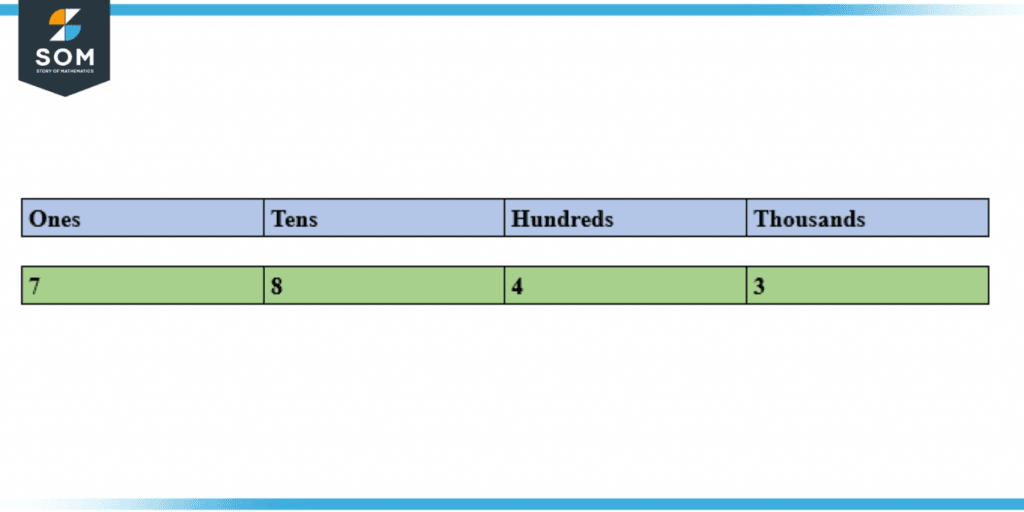
Figure 4 – Decimal Places in Example 1
Solution
In this example, the number represented is 3487, where 7 is in the ones place, 8 is in the tens place, 4 is in the hundreds place, and 3 is in the thousands place.
Example 2
Can the decimal point help make measurements more precise as compared to using just whole numbers?
Solution
The metric system measures length in meters and weight in grams. To make more precise measurements, decimal points are used to indicate the position of the digits.
For example, on a fully whole numbered scale, a person can only weigh 70 or 71 kg, but we know that this is not necessarily accurate. In most modern scales, weights are measured up to two or even three decimal places. On such scales, a person may weigh 70.5 kg, which is a much more precise and accurate measurement of the person’s exact weight.
Similarly, a room might be 3.25 meters long, which is clearly three and a quarter meters. Therefore, the added fractional part really helps make measurements a lot more precise and useful, which makes that information more useful.
Example 3
Break down the number 12.34 into its individual parts, and explain the positioning and place value of the digits before and after the decimal point.
Solution
In the number 12.34, the “4” is in the hundredth place, and the decimal point separates the whole number “12” from the fractional part “34“.
The position of a digit in a decimal number is determined by its place value, which is determined by the position of the digit relative to the decimal point. The place value of a digit to the left of the decimal point represents the number of ones, tens, hundreds, etc. The place value of a digit to the right of the decimal point represents the number of tenths, hundredths, thousandths, etc.
For example, in the number 12.34, the digit “1” has a place value of 101 (ten), the digit “2” is in the place of ones, so it has a place value of 100 (one), the digit “3” has a place value of 10-1, and the digit “4” has a place value of 10-2 (a hundredth).
All the figures above were created on GeoGebra.