Decimal Fraction|Definition & Meaning

What Is a Decimal Fraction? 

A fraction is said to be decimal if the fraction’s numerator is a power of 10, such as 10, 100, 1000, 10000, etc., and the denominator is also a power of 10. The relationship between a part and its total is described by the term “fraction.” Therefore, the entire is always divided into parts equal to a power of 10, such as 10, 100, 1000, and so on, whenever a decimal fraction is used.

For example, 7/10 suggests that we only consider 7 of 10 aspects of the problem. Firstly, converting a decimal to a fraction is to write the denominator as a power of 10, in which the number of zeros will be equivalent to the number of decimal places in the number that was given.

Adding Decimal Fractions

There are two ways, both of which are described in more detail below that you can add two or more decimal fractions:

First, the decimal fractions are converted to similar fractions, and then they are added.

Using the first approach, we begin by converting decimal fractions to pure decimals, and then we proceed to add the resulting numbers. For instance, let us add 2/10 + 34/100. Two-tenths, written as 0.2, are equivalent to thirty-four one-hundredths, written as 0.34. Now, 0.2 + 0.34 = 0.54. Consequently, 2/10 and 34/100 are added together to equal 0.54, which can also be represented as 54/100.

To demonstrate, let us add the same values using the second approach. Find the least common multiple of the denominators to change the provided fractions, 2/10 and 34/100, into fractions with the same value. The number 100 is the least frequent multiple of both 10 and 100. Multiplying the numerator and the denominator of 2/10 by 10 will get you the answer.

2/10 = (2 × 10)/(10 × 10)

2/10 = 20/100

Now, 20/100 + 34/100 = 54/100.

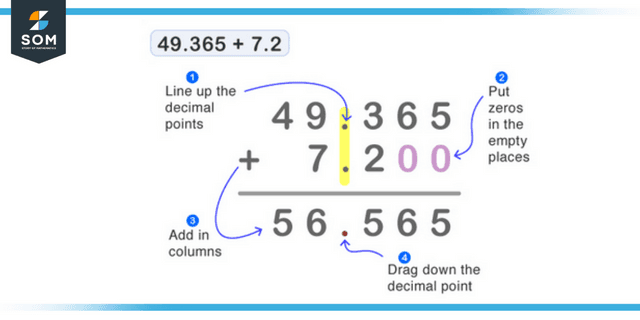
Figure 1: Representation of adding method of decimals

Subtracting Decimal Fractions

The process of subtracting decimal fractions from whole numbers follows the same steps as adding them. For instance, the problem 44/100 – 1/10 can be solved by writing the equation as 0.44 – 0.1, which results in the value 0.34, which is the same as 34/100.

Firstly finding the least common multiple of the denominators and converting them into fractions with like denominators is an additional method for subtracting 1/10 from 44/100. The least significant digit of 100 and 10 is 100. Multiplying the numerator and the denominator of 1/10 by 10 will get you the answer.

1/10 = (1 × 10)/(10 × 10)

1/10 = 10/100

Now:

44/100 – 10/100 = 34/100

Performing Multiplications on Decimal Fractions

When multiplying decimal fractions, you must first independently multiply each fraction’s numerator and denominator components. Adding the number of zeros is required to multiply powers of 10. For instance, 7/10 multiplied by 3/100 is (7 3) divided by (10 100), which equals 21/1000.

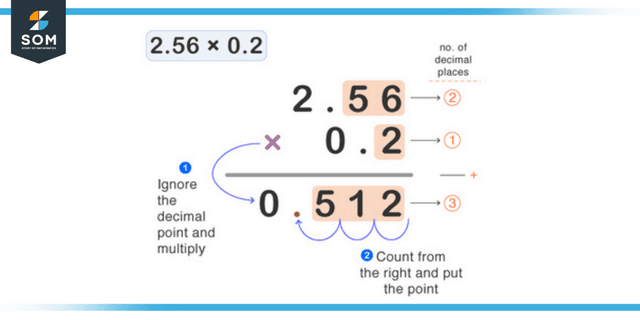
Figure 2: Representation of multiplication method of decimals

Calculating Divisions Using Decimal Fractions

The following steps must be followed to divide two decimal fractions:

Firstly, locate the inverse of the second fraction.

The second step is to do a multiplication using the first fraction and the inverse of the second fraction. That will be the appropriate response to provide.

This is equivalent to performing a standard division of fractions. For instance, 25/10 multiplied by 5/100 equals 25/10 times 100/5. Therefore, 5 times 10 is equal to 50. Therefore, 25/10 multiplied by 5/100 equals 50.

Types of Decimal Fractions

Based on the number of decimal places they include, decimals can be divided into the following categories:

• Terminating decimals
• Non-terminating decimals that recur indefinitely
• Decimals that do not repeat themselves and do not terminate

When it comes to decimal fractions, we are aware that every decimal fraction may be represented as a decimal, with the number of decimal places being equal to the number of zeros in the power of 10 written in the denominator. This is a well-known fact. Therefore, decimal fractions are considered examples of the type of decimal known as terminating decimals.

Conversions Between Decimal and Fractions

It is possible to convert a fraction to a decimal form if the fraction’s denominator can be stated in the manner of prime factorization using either 2 or 5, or both.

For instance, the denominator of the fraction three-quarters is four. It is possible to factor the number 4 as 2 times 2. Therefore, it is possible to convert this fraction to a decimal fraction. Since then is not a multiple of four, we shall proceed to the following power of ten, which is 100.

The number 100 is the 25th multiple of the number 4. Because of this, to turn 3/4 into a decimal fraction, we will need to multiply the numerator and the denominator by 25. It may be deduced from this that 3/4 = (3 25)/(4 25) = 75/100. Let us consider one more example.

However, there is another way for us to turn it into a decimal fraction. Divide 5 by 12. You should expect to receive around 0.42. A value of 0.42 is equal to 42/100. We can figure out how to convert a decimal to a decimal fraction.

Step 1: Determine the number of decimal places in the decimal number.

Step 2: Take away the decimal point from the number, and then divide it by a power of 10 such that the number of zeros equals the number of decimal places counted in Step 1.

Let us convert 0.42 to a fraction. 0.42 has two decimal places. This indicates that we must divide it by 100, the second exponent of 10, to get the answer (102). As a result, 0.42 equals 42/100.

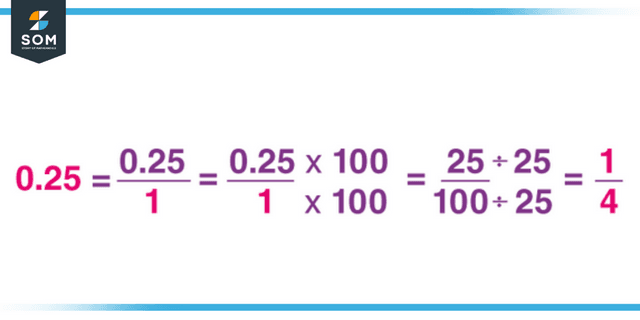
Figure 3: Conversion between decimal and fraction

Some Examples of Decimal Fractions

Example 1

In a class test of total 10 marks, student 1 get 8.5, student 2 get 6.75 and student 3 get 9.5 marks. What is the average of their marks?

Solution

8.5 + 6.75 + 9.5 = 24.75

24.75/3 = 8.25

Example 2

What is the decimal value of 36/10?

Solution

Dividing 36 by 10, we will get 3.6.

All images/graphs are created using GeoGebra.

Debit Definition < Glossary Index > Decimal Point Definition