Degree (Angles)|Definition & Meaning

In a plane with only two dimensions, an angle that measures one degree is referred to as a degree angle. Itt is one of the most frequently employed metrics to express the overall magnitude of angles in two-dimensional shapes. In geometry, trigonometry, and many other subfields of mathematics, a degree angle is a standard unit of measurement.

It is common practice to express the angle in terms of an arc length, which refers to the total distance traveled around the circumference of a circle that the angle subtends. For instance, traveling a quarter of the length of a circle corresponds to a 90 degrees movement around the circle.

Diagrammatic Representation of the Degree Angles

The following figure represents the one complete rotation of the circle, which is equal to 360 degrees. Each quarter is 90 degrees. 

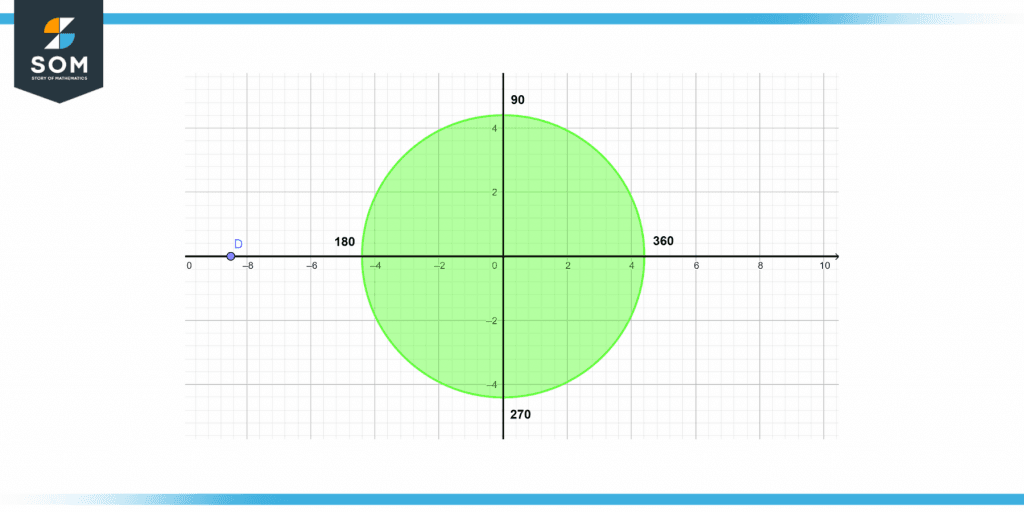
Figure 1 – Complete representation of degree angle

The different angles of the degree angle system are represented in the following figure.

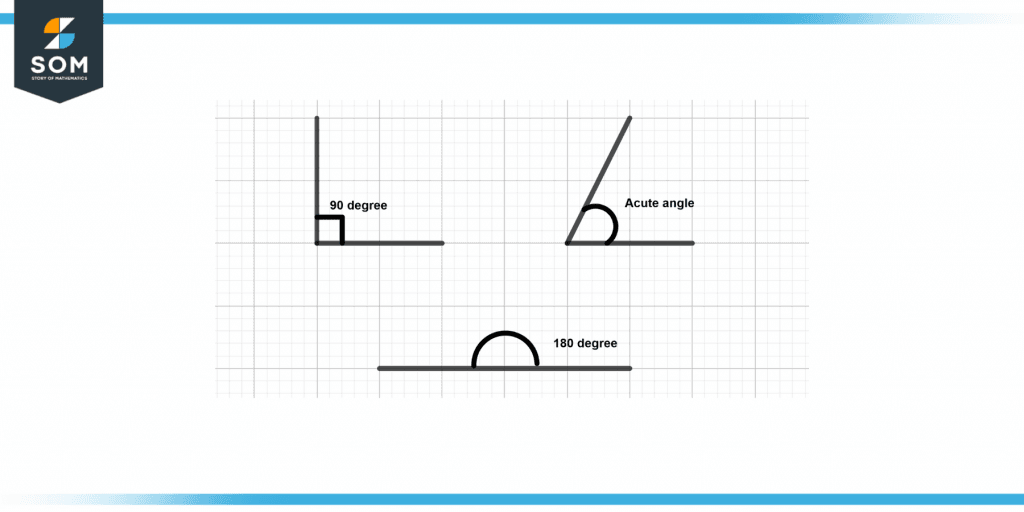
Figure 2 – Different angles of degree system

The following plot shows the degrees that are present in each quarter. Each of the four quarters has a degree angle of 90. To get from point A to point B, you will need to turn through an angle of 180 degrees to accomplish what you set out to do.

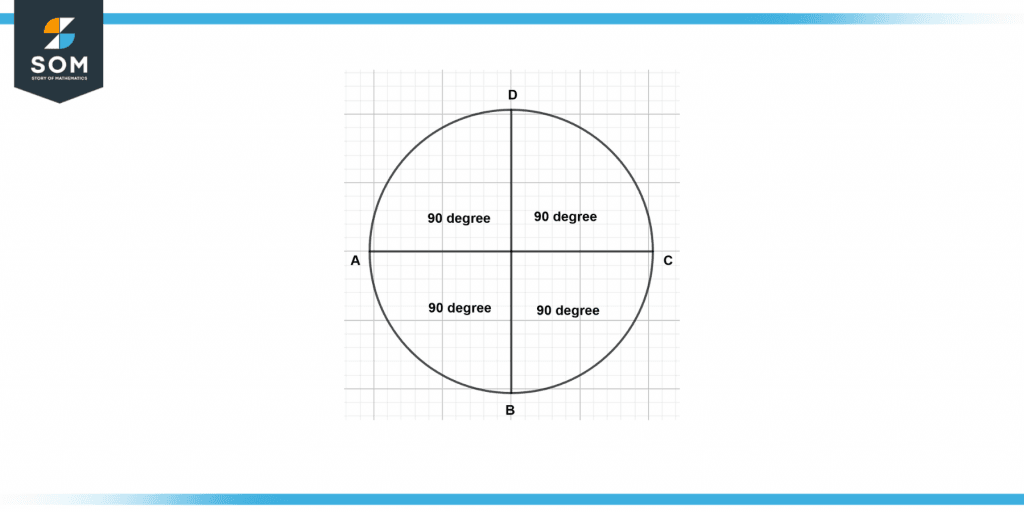
Figure 3 – Degree representation for each quarter

What Is an Angle in Degrees?

One of the most fundamental and crucial ideas in geometry is the concept of a degree angle. It measures both the size and the form of an angle. The measurement of an angle formed by two lines meeting at a common point is sometimes referred to as a “degree angle.” It can also be used to indicate the size of an angle created when an object is rotated by a certain degree.

The amount of rotation around a point equals one degree. The angle created by this rotation, which is expressed in degrees, is known as a degree angle. One degree of an angle is equivalent to 1/360th of a circle since a whole circle has 360 degrees.

The most frequent angle is a right angle, which is 90 degrees. Because it is used to determine the size and shape of angles and other objects, the degree angle plays a significant role in geometry.

In trigonometry and other mathematical applications, degrees are also used to measure angles. Everyday life also makes use of the degree angle. To ensure that a window or door frame fits properly, the angle of the frame is measured.

Applications of Degree Units in Angle Measurements

There are many applications for the degree angle in mathematics and science, as it is a standard unit of measurement for angles.

The angles of various geometric figures, such as triangles and circles, are measured in degrees. Trigonometry is the branch of mathematics that uses measurements in terms of angles to determine other quantities, such as lengths, distances, and even slopes and heights.

Stars, planets, and other heavenly bodies can all have their positions and orientations determined using degree angles. Forces, velocities, and accelerations in physics are all measured in terms of degrees of angle.

Degree angles have practical applications beyond the scientific realm as well. Cake pan angles, for instance, can be measured in degrees for more precise results. In the same way, builders utilize degree angles to set the pitch of a building’s walls, roof, and other components.

Chair and table angles, as well as other furniture angles, can be measured in degrees. Clothing measurements, such as the angle of a neckline or sleeve, can also be expressed in degrees.

Distinction Between Radians and Degrees

Radians and degrees are both angle measurement units that are used to calculate the size of angles and arcs in circles. The conversion factor is the primary distinction between both. Radians are the standard unit of angle measurement in mathematics and physics, and they are based on the radian, the natural unit of a circle.

A radian is basically the angle subtended by an arc on a circle where the length of the arc is equal to the circle’s radius.

In other words, if you draw a circle with a unit radius and an arc with a length of one on it, the angle subtended by the arc is one radian. This definition assumes that a whole circle has an angle of 2 radians. Conversely, degrees are the conventional unit of angle measurement in common use and are based on the ancient Babylonians’ sexagesimal system.

A degree is one-third of a whole circle. This signifies that the angle of a whole circle is 360°/180 is the conversion factor between radians and degrees.  Because the measurement is based on the natural unit of a circle, radians are commonly used in mathematics and physics, where precision is critical. Because degrees are easy to use and understand, they are commonly utilized in everyday applications such as navigation.

Furthermore, radians and degrees both measure angles in distinct ways. Radians measure angle size based on the length of an arc on a circle, whereas degrees measure angle size based on a fraction of a full circle. This means that the same angle can be measured in radians and degrees in various ways.

Numerical Example of Angle Conversion from Degrees to Radians

What is the equivalent of 180 degrees in radians?

Solution

To convert it into radians, we know that:

angle in radians = angle in degrees x ($\pi$ radians / 180 degrees)

By putting values, we get:

180 degrees in radians = 180 x ($\pi$ / 180)

180 degrees in radians = $\pi$ radians

All images/mathematical drawings were created with GeoGebra.

Degree Algebra Definition < Glossary Index > Degree Temperature Definition