JUMP TO TOPIC
Degree Algebra|Definition & Meaning
Definition
Degree Algebra is defined as the highest valued power of a variable in a polynomial expression while ignoring the coefficients. We can also find the sum of all the variables to get the highest degree of the expression.
Significance of Degree Algebra
Degree Algebra is the highest power of any polynomial expression when represented in its standard form. A polynomial is either the sum or difference between two or more than two algebraic expressions which have different exponents. To differentiate between polynomials we use degree algebra. The highest power of a variable is the degree in any expression.
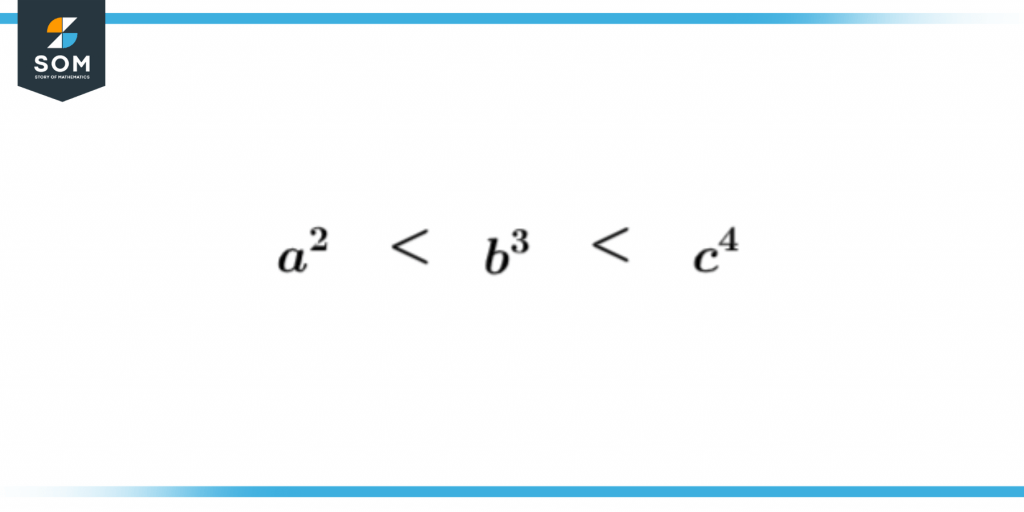
Figure 1 – Powers of variables in ascending order
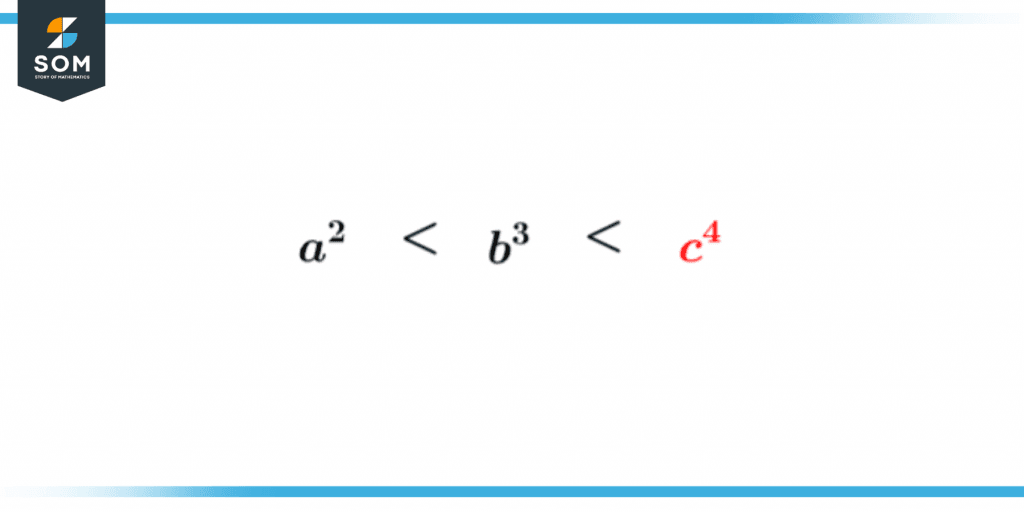
Figure 2 – The variable with the highest power represents the Degree
The importance of the degree of an expression can be summarized as follows:
- We can find the homogeneity of any polynomial expression by finding the degree of each term.
- The sub-types of polynomials have been defined based on the degree.
- The degree of an expression lets us know how many possible solutions can be calculated.
- While drawing a graph we use this concept to get accurate results.
Calculating the Degree of an Expression
Let us understand this concept better by looking at the following expression:
\[ 6x^2 + 2x^3 + 1\]
To find the degree of this expression we combine all of the like terms which can be determined by their variables. After that, we will arrange all these terms in descending order for our ease. To find the degree all of the coefficients must be ignored as they are irrelevant while finding the degree of a polynomial.
\[ 2x^3 + 6x^2 + 1 \]
Once this is done we can list the following:
\[2x^3 , \text{ Value} = 3\]
\[6x^2, \text{ Value} = 2\]
\[1, \text{ Value} = 0\]
Now the largest power will be the degree of this polynomial expression which is 3 in this case
Now to find the degree of this expression we will add the exponents together:
3 + 2 + 1 = 6
Hence the overall degree of this expression is 6.
To expand our knowledge further we will now find the degree for multivariable polynomials. Multivariable polynomials are defined as such types of polynomials where there is more than one variable in an expression. In such a case we add the exponents together where each exponent will be considered as a whole number.
Let us consider the following example:
\[ 4x^4y^2 + 7x^3y^2 – 34 \]
In this expression, we see 2 variables, x and y. So we will find the degree by adding each variable in a term to find the total degree. We can say that:
\[4x^4y^2 , \text{ Value}= 6\]
\[7x^3y^2, \text{ Value} = 5\]
\[34, \text{ Value} = 0\]
So the degree of this polynomial expression is 6.
Degree of Zero and Constant Polynomials
When all of the coefficients of a polynomial are zero, it is called a zero polynomial. If we have to tackle with a zero polynomial in any expression then we either consider it as undefined or its value is set to -1.
Constant polynomials are those terms in any expression which do not contain any variable with them and have constant values. As there is no variable so we consider their power to be equal to zero.
\[ f(x) = 2 \]
Its polynomial form will be:
\[ f(x) = 2x^0 \]
Illustrating the Degree Finding Process
Let us now understand the concepts of degree algebra through a pictorial format. Considering the following expression:
\[ 7x^3 + 4x^2 + 5 \]
In this expression, the algebraic degree will be the highest valued exponent. For that, we will follow the same steps which are; ignoring the coefficients, arranging all terms in descending order, and finding the degree of the expression.
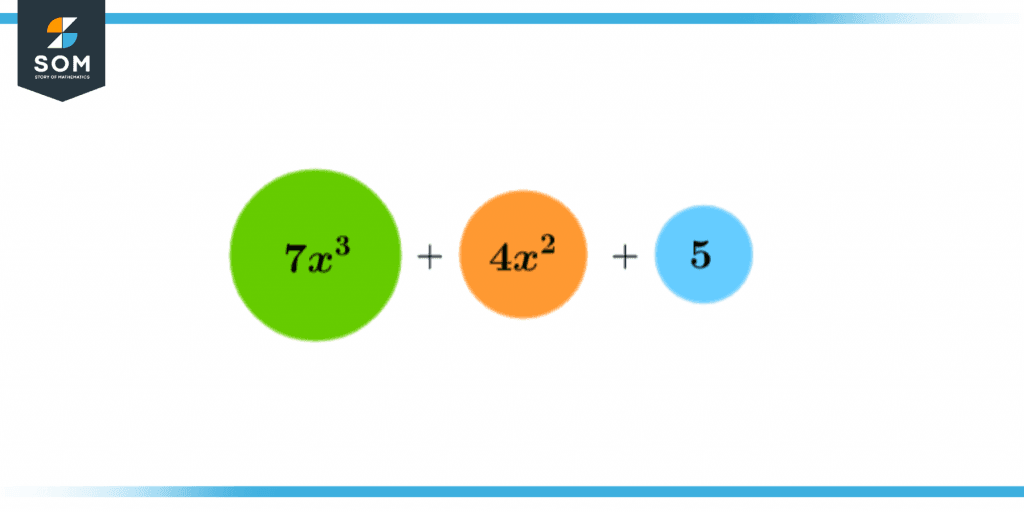
Figure 3 – Exponential Values of an Expression (larger circles represent the larger power)
In this figure, we have represented the value of each degree by the size of a circle for our better understanding. We can see that the first term is having the algebraic degree and is represented by the biggest circle compared with the number 5 which has the smallest circle meaning it has the smallest value of the exponent.
If we go further into multi-variables we can also find its degree by following the same methods. Let us look at the following example:
\[ a^3b^2 + a^3b^3 + a^2b^2 + a^2b \]
In this example, we will add the powers of both a and b to get the complete value of the exponent. The term with the highest value of exponent will be the degree of the expression.
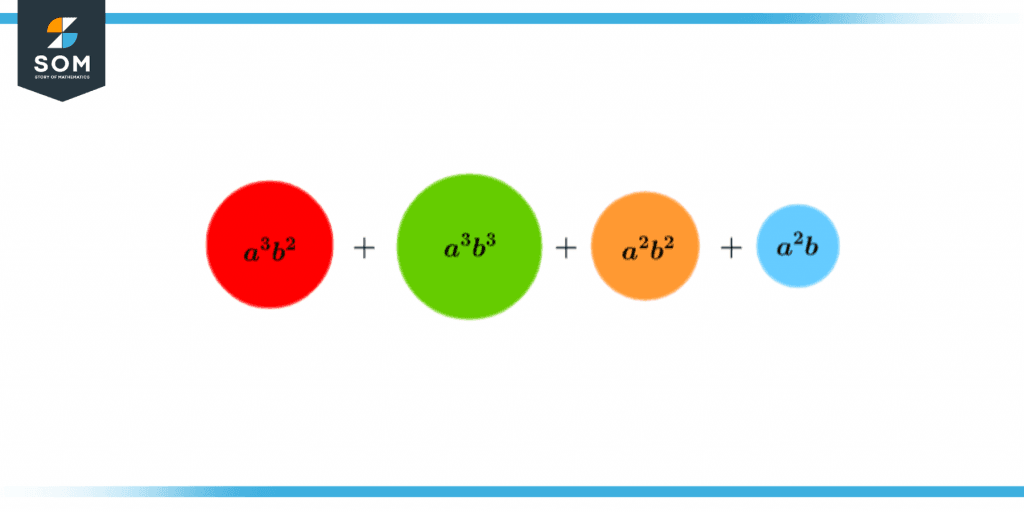
Figure 4 – Exponential Values of Multivariable Polynomials (larger circle represents larger degree)
This figure shows the size of each term based on its exponent’s value. The term with the highest value is:
\[a^3b^3 \]
So the degree of this expression is 6.
Solved Examples of Degree Algebra
Example 1
Josh’s math teacher has assigned him extra homework to improve his grades. Help him find the degree of each expression so that he can pass.
\[ 7x^6 + 13x^2 + x^3 + 4x^5 + 1 \]
\[ 3x^2 + 3y^3 + 3z^4 + 3x^5 + 3 \]
\[ 7x + 13y + 1 \]
Solution
In these expressions, we can find the degree by following the same methods.
- The degree of this equation is 6
- The degree of this equation is 5
- The degree of this equation is 0
Example 2
Solve and explain the following expression to find its degree.
\[ 8x^2 + 7x^3 + 2x^2 + 4x^5 + 5x^3 + 3 \]
Solution
Firstly we will arrange the terms according to their exponential values
\[ 8x^2 + 2x^2 + 7x^3 + 5x^3 + 4x^5 + 3 \]
Then we will group and solve the terms having the same exponential values
\[ (8x^2 + 2x^2) + (7x^3 + 5x^3) + 4x^5 + 3 \]
\[ 10x^2 + 12x^3 + 4x^5 + 3 \]
Now we will ignore all of its coefficients to find the degree
\[ x^2 + x^3 +x^5 + 3 \]
From this expression, we can say that the algebraic degree is 5.
Example 3
Find the degree of the following expression and explain your answer.
\[ x^2 + 2x^3 +x^6 \]
Solution
The degree of this expression is 6. The degree of an expression must always be of positive variables and never a negative variable.
Images/mathematical drawings are created with GeoGebra.
