Determinant|Definition & Meaning

Square matrices have an equal number of rows and columns. Thus, if the number of columns is n, then the number of rows must also be n, as illustrated below: 

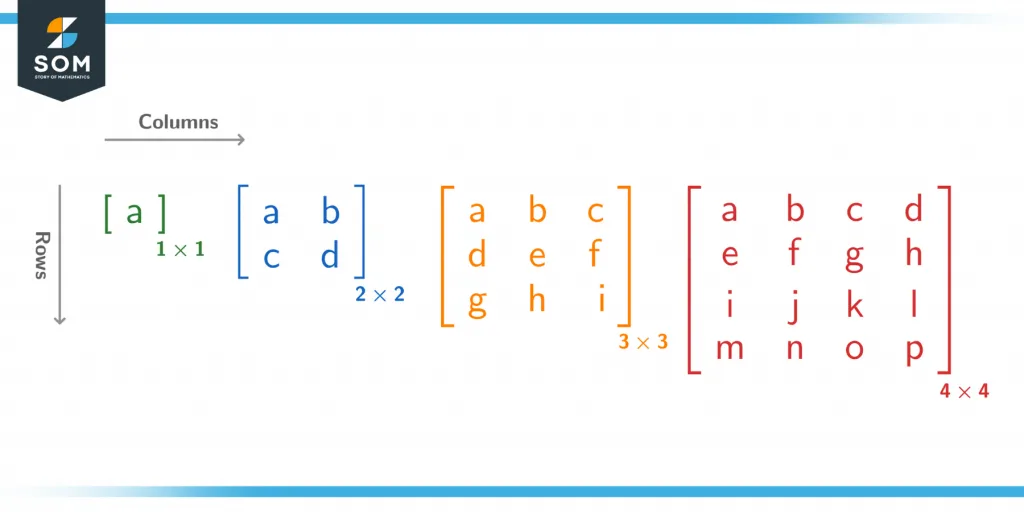
Figure 1 – Square matrices of increasing order.

Finding the Determinant

There are a few methods to calculate the determinant. By definition, the determinant is found using the Laplace Expansion method. Without getting too technical right away, we illustrate the process for 1×1 square matrices and higher.

1×1 Matrix

A 1×1 matrix is essentially a single scalar value. The determinant is the value itself. Very simple!

\[ A = \begin{bmatrix} \,a\, \end{bmatrix} \Rightarrow |A| = a \]

2×2 Matrix

We illustrate the process and formula for the determinant of a 2×2 matrix in the figure below.

Figure 2 – The determinant of a 2×2 matrix is the difference between the products of the primary and secondary diagonal.

3×3 Matrix

For this, we need to expand along the first row. The steps are mentioned and illustrated below:

1. Write out the determinant form (optional).
2. Take the first element along the row (blue and circled in figure) and find the 2×2 sub-matrix that does not contain the elements in its row and column (blue background in figure). Repeat for the second and third elements.
3.  Multiply the element with the determinant of its corresponding sub-matrix. You now have three terms: add the first, subtract the second, and add the third. This order is important!
4. Write the determinant of the 2×2 sub-matrices in expanded form and evaluate the result.

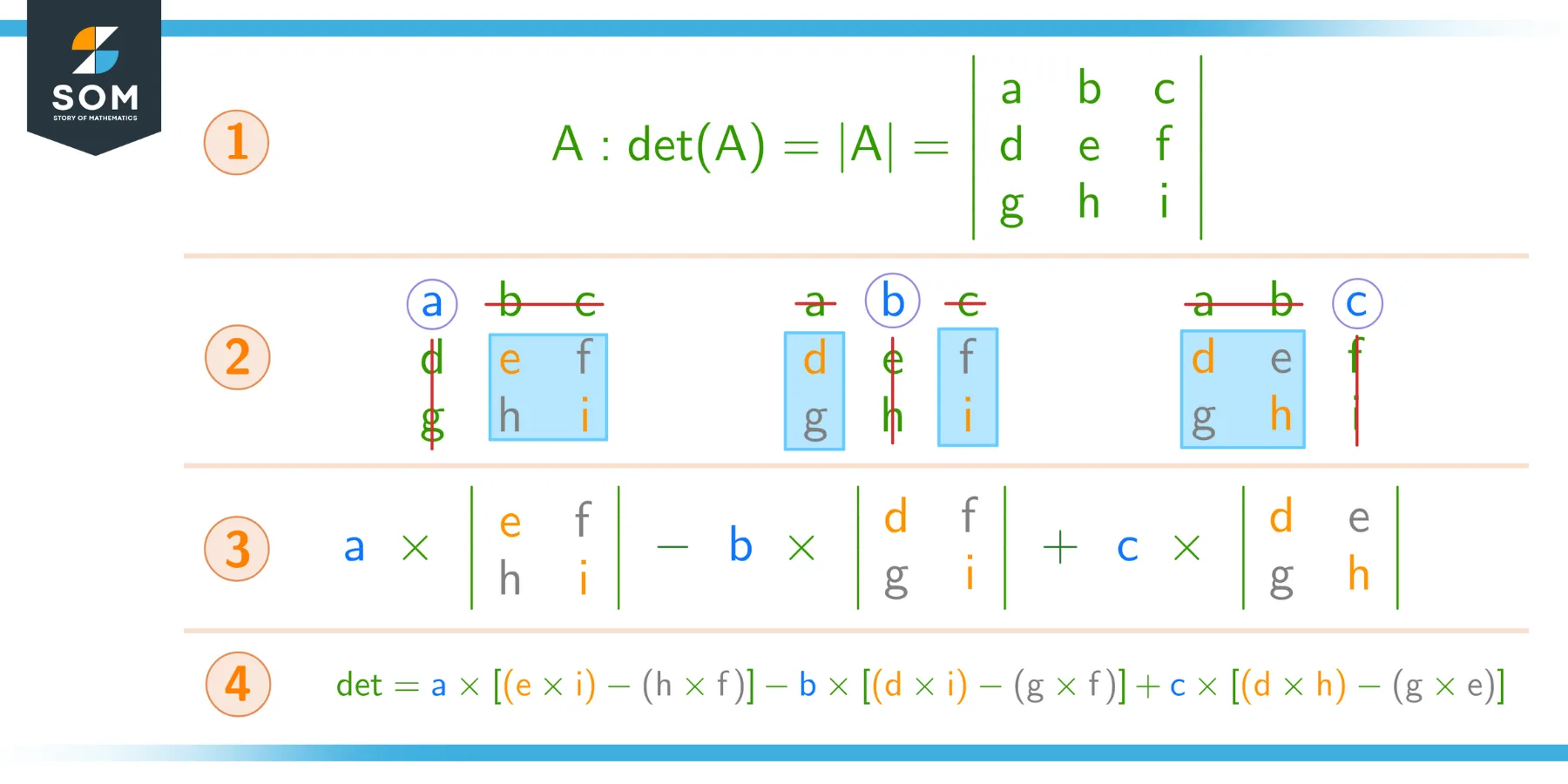
Figure 3 – Calculating the determinant of a 3×3 matrix by expanding along the first row.

If you apply the same process to the 2×2 matrix, you will still arrive at the correct result. In that case, the sub-matrix will be a 1×1 matrix (a scalar value).

4×4 and Higher-order Square Matrices

By now, we have established a pattern that we can use to find the determinant of higher-order square matrices. When expanding over the first row, the determinant has as many terms as the elements in that row. Therefore, we need two things:

1. The sign of each term.
2. The sub-matrix (or “minor”) of each element in the row.

The second one is easy enough. However, we must dive deeper and formally define the determinant for the first part.

Formal Definition of Determinant

The Laplace Expansion definition for the determinant (for expansion along the first row) is formulated as:

\[\text{det}(A) = |A| =\sum_{k\,=\,1}^{n} \left(-1\right)^{k+1} \times \left| A_{1,\, k} \right| \times a_{1, \,k}\]

Here, $a_{1,\,k}$ denotes the k^th entry in the first row (you can think of k as the column number), and $A_{1,\,k}$ represents the minor (sub-matrix) with the first row and k^th column removed. The term $(-1)^{k+1} \times \left| A_{1, \,k} \right|$ is called the “cofactor.” 

Determining the Sign

The $(-1)^{k+1}$ term from the formula assigns the sign to each expanded term in the determinant’s expression. It is simple: even-numbered entries have the minus, while odds have the plus. 

However, this is true only for expanding the first row. The truly general pattern is that if (i, k) represents the row and column number of the expanding element, then if:

• i + k = even, sign = positive
• i + k = odd, sign = negative

You can see this is true by checking the expansion of the first row. The first entry has (i, k) = (1, 1) and 1 + 1 = 2, which is even, so this term has a positive sign. There is a useful visual mnemonic to remember this alternating plus-minus pattern, which we illustrate below:

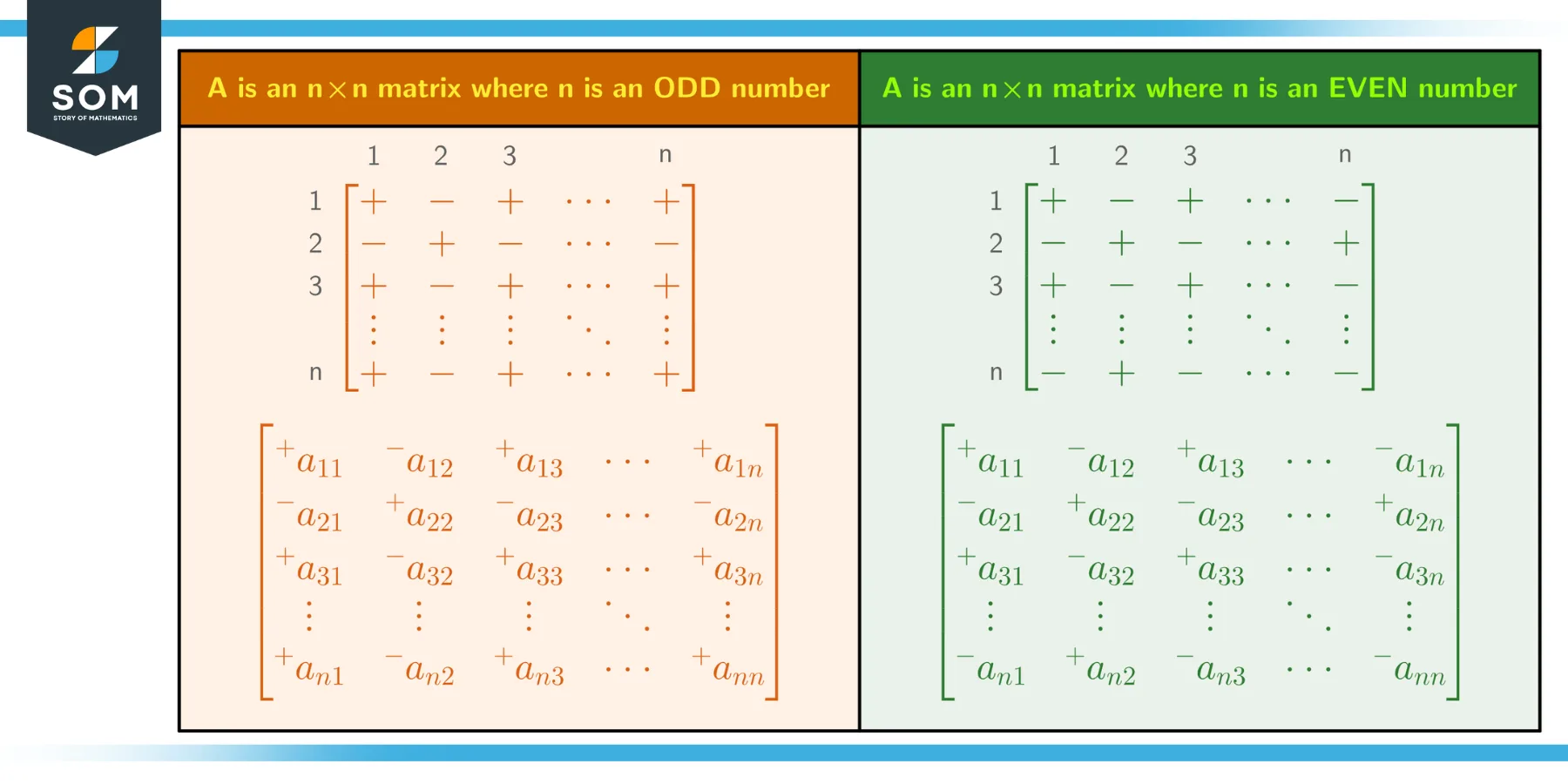
Figure 4 – A visual representation of the alternating plus-minus patterns created by the $(-1)^{i+k}$ term in the generalized Laplace expansion of a matrix.

Thus, if A is a 4×4 matrix:

\[ A = \begin{bmatrix} \,a & b & c & d\, \\ \,e & f & g & h\, \\ \,i & j & k & l\, \\ \,m & n & o & p\, \end{bmatrix} \]

The row and column numbers for the first row’s elements are a = (1, 1), b = (1, 2), c = (1, 3), and d = (1, 4). Thus, the signs for a, b, c, and d are respectively +, -, +, and -. The determinant of A would be:

\[ |A| = a \times \begin{vmatrix} \,f & g & h\, \\ \,j & k & l\, \\ \,n & o & p\, \end{vmatrix}-b \times \begin{vmatrix} \,e & g & h\, \\ \,i & k & l\, \\ \,m & o & p\, \end{vmatrix}+c \times \begin{vmatrix} \,e & f & h\, \\ \,i & j & l\, \\ \,m & n & p\, \end{vmatrix}-d \times \begin{vmatrix} \,e & f & g\, \\ \,i  & j & k\, \\ \,m & n & o\, \end{vmatrix} \]

We can extend this procedure to any nxn square matrix.

Calculating the Determinant by Expanding Other Rows and Columns

We do not need to always expand along the first row. It is often more convenient to expand along another row or column in the matrix (e.g., the second row has more zeros, which would simplify the calculation). For that, we need to keep a few things in mind, as discussed below.

Determinant by Expanding Other Rows

We can extend the original Laplace Expansion for the determinant to expand along any row ‘i’ as:

\[ \text{det}(A) = |A| = \!\!\!\!\!\!\!\!\!\! \sum_{\substack{k\,=\,1 \\ i\,\in\,\{1,\,2,\,\dots,\,n\}}}^{n} \!\!\!\!\!\!\!\!\! \left(-1\right)^{k+i} \times a_{i,\,k} \times \left| A_{i,\,k} \right| \]

Since the method to find the minor does not change, we can similarly expand from any row other than the first as long as we remember the plus-minus patterns. We illustrate the process for expanding a 3×3 matrix using the second row below:

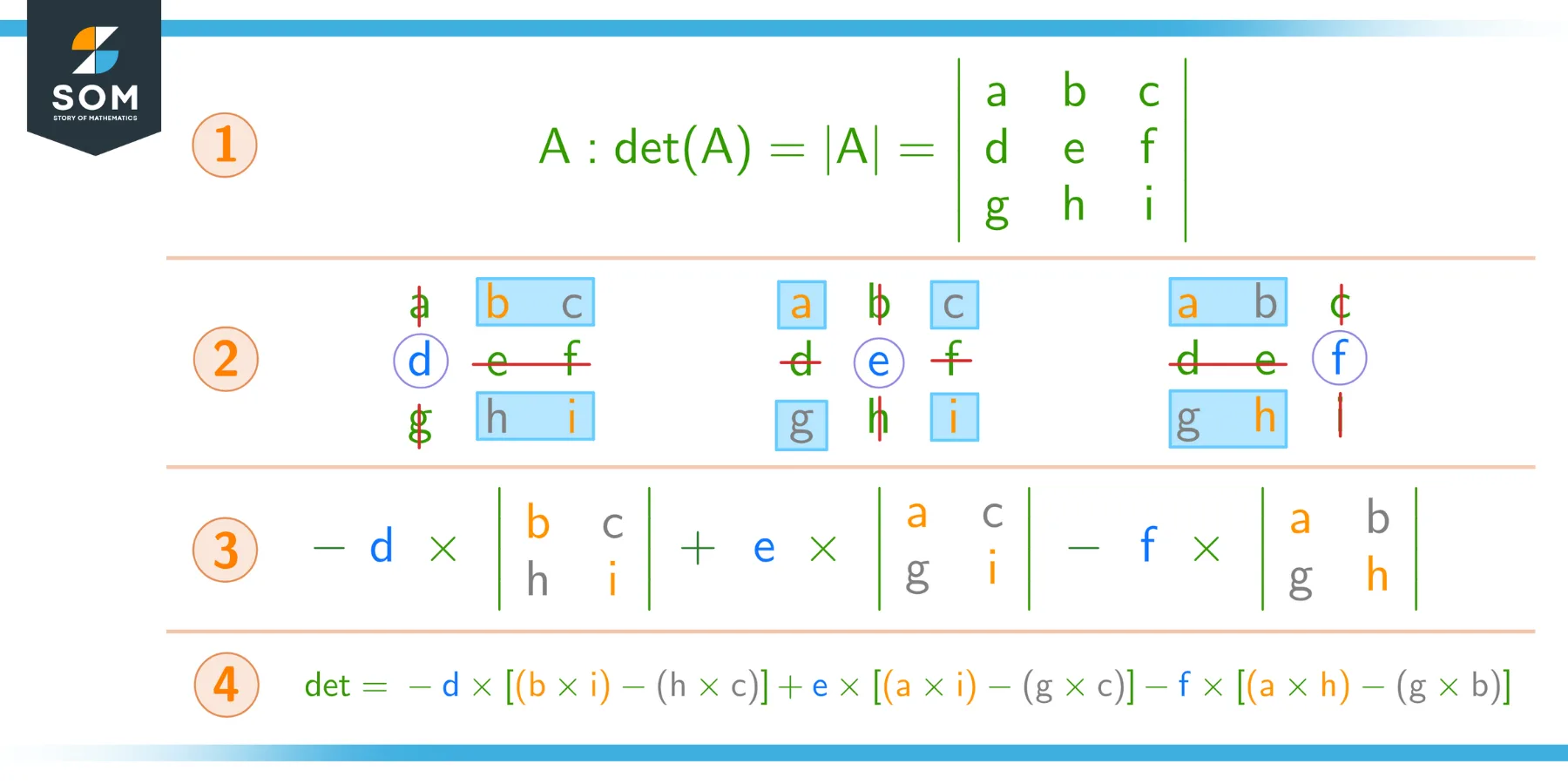
Figure 5 – Finding the determinant using Laplace expansion over the second row. Notice the sign changes compared to Figure 3 and verify this from the mnemonic in Figure 4.

Determinant by Expanding the Columns

Formally, we can extend the definition of the Laplace Expansion to the first column:

\[\text{det}(A) = |A| =\sum_{i\,=\,1}^{n} \left(-1\right)^{i+1} \times \left| A_{i,\,1} \right| \times a_{i,\,1}\]

Here, ‘i’ represents the i^th row. Similarly, we can expand along any column ‘k’ as:

\[ \text{det}(A) = |A| = \!\!\!\!\!\!\!\!\!\! \sum_{\substack{i\,=\,1 \\ k\,\in\,\{1,\,2,\,\dots,\,n\}}}^{n} \!\!\!\!\!\!\!\!\! \left(-1\right)^{i+k} \times a_{i,\,k} \times \left| A_{i,\,k} \right| \]

All that changed was the notation order (reflecting that the row number changes instead of the column number now).

Again, we must remember the plus-minus patterns. The minor-finding process remains the same.

An Example of Calculating the Determinant

Find the determinant of the following matrix:

\[A = \begin{bmatrix} \,3 & -1 & 0\, \\ \,2 & -2 & 3\, \\ \,9 & -3 & 0\, \end{bmatrix}\]

Solution

Expanding from the third column (it has two 0s, so the calculation will be easy):

\[ |A| = 0-3[3(-3)-9(-1)]+0 = 3(-9+9) = \mathbf{0} \]

A matrix with a zero determinant is called a singular matrix. The inverse of such a matrix does not exist.

Additionally, we can verify our result using the fact that when any two rows or columns of a matrix are multiples of each other (the first and third rows in our case), the determinant is zero.

Reason: Row-order operations simplify such a matrix to have one row or column completely 0. Since the determinant is constant for a given matrix and can be found by expanding any row or column, having a row full of zeros means the determinant must be zero.

All images/mathematical drawings were created with GeoGebra.

Deposit Definition < Glossary Index > Deviation Definition