Diagonal|Definition & Meaning

Figure 1 shows the demonstration of diagonals in different colors. The line segments AB, CD, and EF are the diagonals in the square, rectangle, and hexagon respectively. 

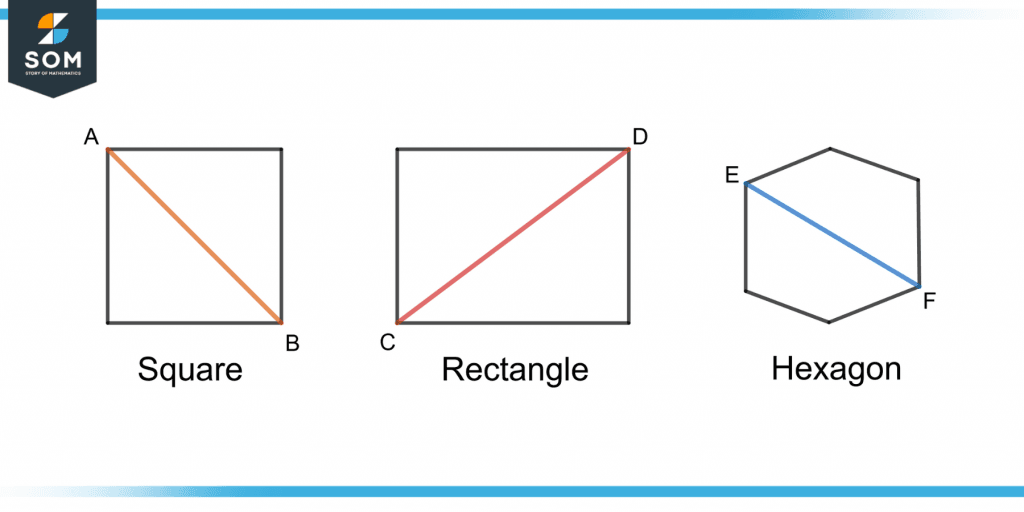
Figure 1 – Demonstration of Diagonals in Square, Rectangle and Hexagon

Historical Background

The word “diagonal” comes from the Greek word “diagonios” which means “from one angle to another”. Euclid and Strabo referred to it as a line joining two opposite vertices of a geometrical shape.

It also comes from the Latin word “diagonus” which means “inclining line”. So from the ancient perspective, a diagonal is a line segment having some slope titled at some angle connecting non-adjacent vertices.

Geometry

Geometry is the field of mathematics that involves the study of different shapes and their geometrical interpretations and calculations. Diagonals were recognized in the early developing stages of geometry.

The following terms play an essential role while understanding the concept of diagonal.

Polygon

A polygon is a geometrical shape consisting of three or more lines. It is a two-dimensional structure whose boundaries are the line segments connected to form a closed figure.

“Poly” means “many” so there can be as many line segments to form its boundary. Figure 2 shows different types of polygons.

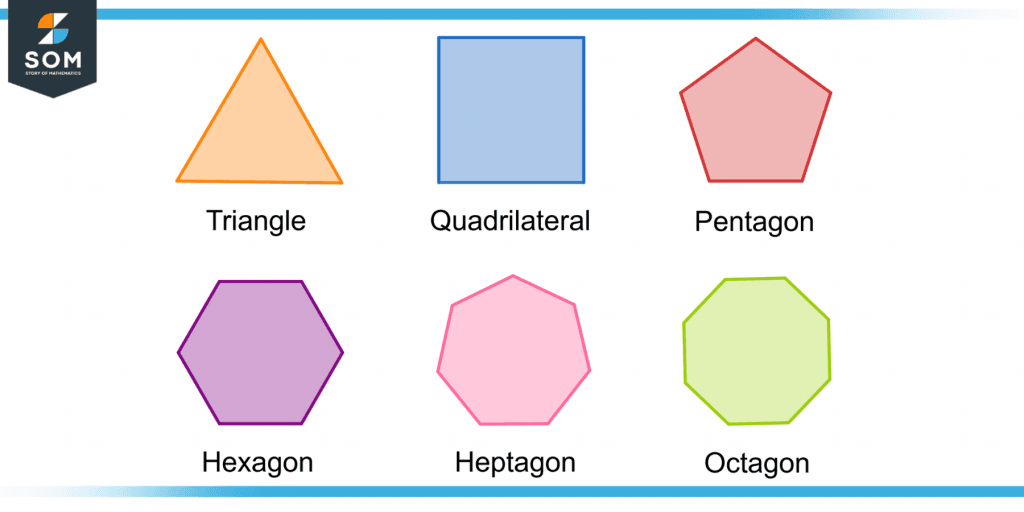
Figure 2 – Different Types of Polygons

Non-adjacent Vertices

The points which join the ends of the two sides of a polygon are known as the vertices. Two sides having a common vertex are known as adjacent sides.

Non-adjacent vertices always form diagonals. These are the vertices that don’t share a common side. They are opposite to each other and are not joined by a common edge.

Figure 3 shows the non-adjacent vertices in some polygons.

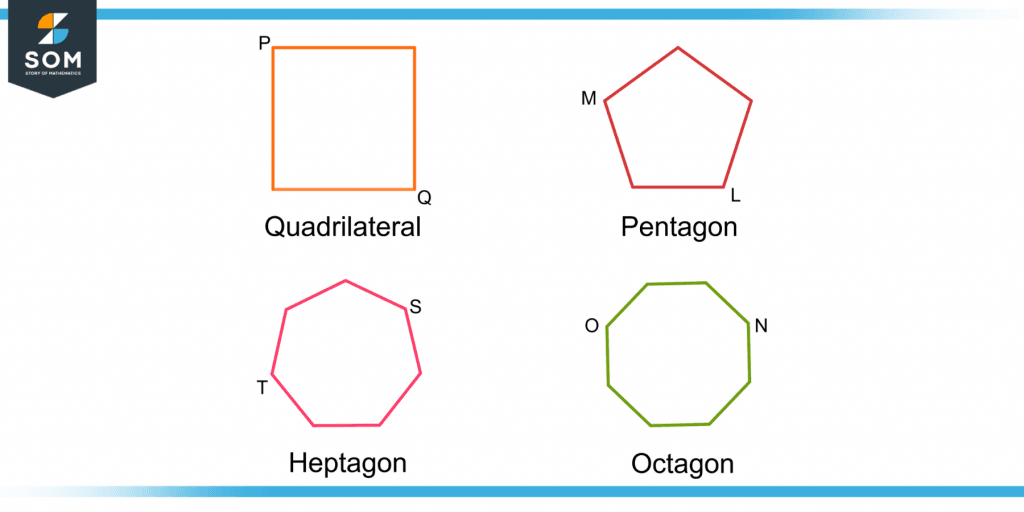
Figure 3 – Non-adjacent Vertices in Different Types of Polygons

Edges

Edges are the sides of a polygon. The adjacent vertices are connected by a line segment that forms a polygon’s edges. The diagonal is not one of these edges.

Concave Polygons

Concave polygons are such polygons that have at least one internal angle greater than 180°. The two sides are bent inwards. Figure 4 shows a concave pentagon.

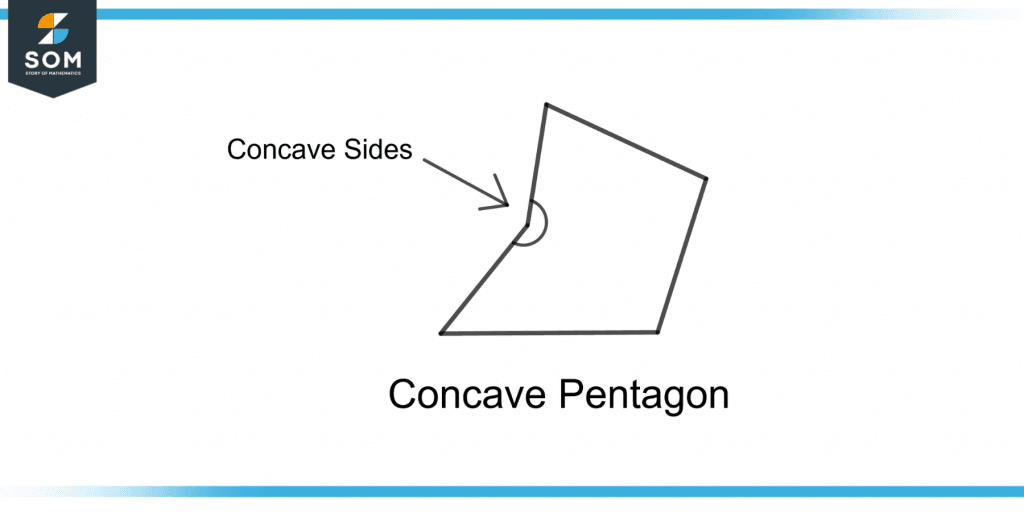
Figure 4 – A Concave Pentagon

Diagonals of Concave Polygon

A concave polygon has a diagonal outside its boundary when drawn from the concave non-adjacent vertices.

Figure 5 shows a diagonal in orange color which is outside the concave pentagon.

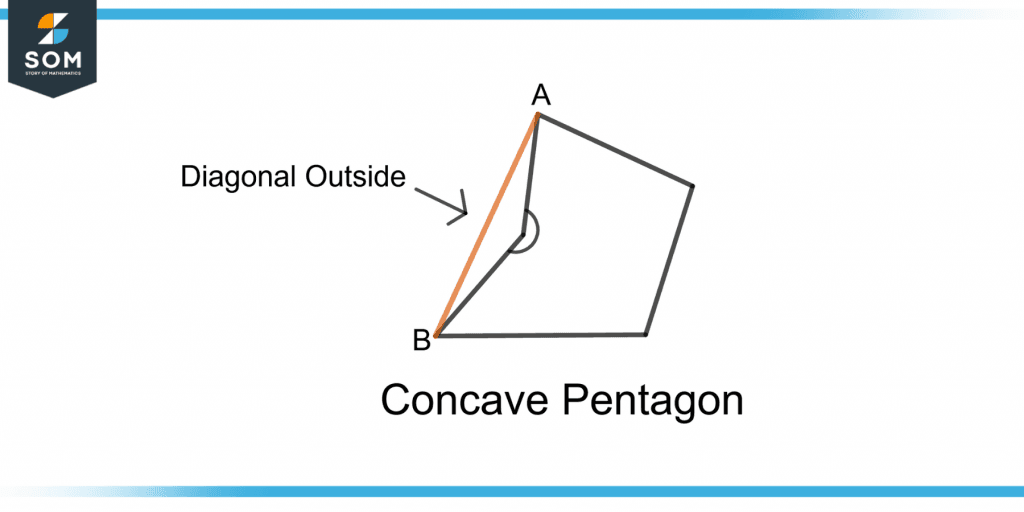
Figure 5 – A Diagonal Outside the Concave Pentagon

Number of Diagonals in Different Polygons

The number of diagonals of a polygon can be calculated by using the formula given below:

No. of Diagonals = n = p(p – 3)/ 2

Where “p” is the number of sides or edges of the polygon. The number of diagonals of the following polygons is calculated.

Triangle

A triangle has no diagonal as the non-adjacent vertices in a triangle are already joined by its edges. This can be proved by using the diagonal formula.

A triangle has three sides, so p will be 3. Putting the value in the above equation gives:

No. of Diagonals in a Triangle = n = 3(3 – 3)/ 2

n = 0

The diagonals are present in the polygons with sides greater than three.

Quadrilateral

For a quadrilateral, p = 4, so the number of diagonals in a quadrilateral will be:

n = p(p – 3)/ 2

n = 4(4 – 3)/ 2

n = 2

So, two diagonals can be formed in a quadrilateral.

Pentagon

A pentagon has five edges, so p = 5, the number of diagonals will be:

n = p(p – 3)/ 2

n = 5(5 – 3)/ 2

n = 5

Hence, a pentagon has five diagonals.

Hexagon

For hexagon,

No. of sides = p = 6

The number of diagonals will be:

n = p(p – 3)/ 2

n = 6(6 – 3)/ 2

n = 9

So, there are nine diagonals in a hexagon.

Heptagon

A heptagon has seven sides, so p = 7. The number of diagonals in a heptagon will be:

n = p(p – 3)/ 2

n = 7(7 – 3)/ 2

n = 14

So, a heptagon has fourteen diagonals.

Figure 6 shows the diagonals in these polygons.

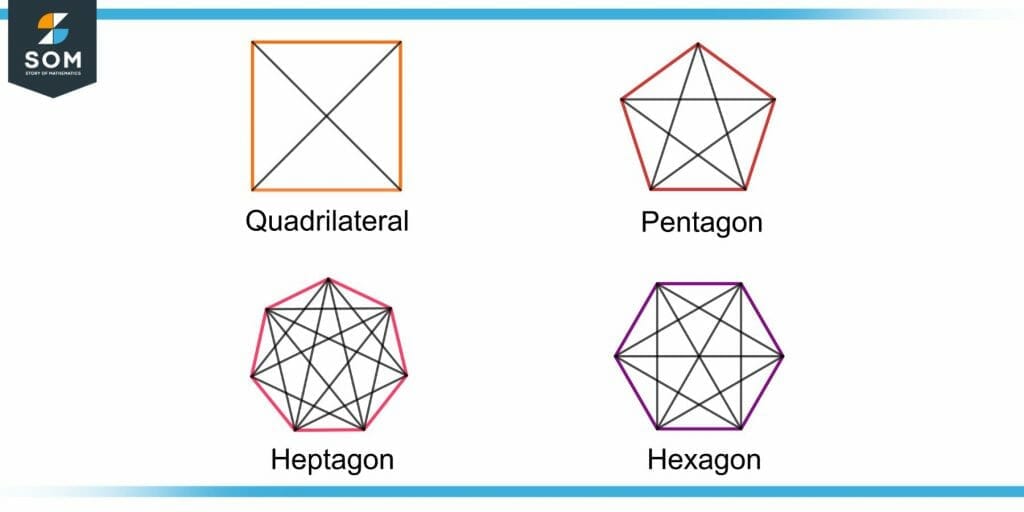
Figure 6 – Diagonals in Different Polygons

Length Calculation of Diagonals in Different Polygons

The diagonal length can be calculated if we know the lengths of the sides in different polygons. Following are some polygons whose length formulas for diagonals are discussed.

Square

A square has equal sides. Let m be the length of a square side; the diagonal length can be calculated with the formula:

Length of Diagonal = d = m$\sqrt{2}$

Rectangle

A rectangle has two sides longer than the other two sides. Let r be the length and s be the breadth of the rectangle. The diagonal length in a rectangle is calculated by using the formula:

Length of Diagonal = d = $\sqrt{ r^2 + s^2 }$

Bisection means dividing into two equal parts. The diagonals of quadrilaterals(square, rectangle, parallelogram) always bisect them.

Solved Examples of Polygons Involving Diagonals

Example 1

Find the number of diagonals in an octagon and a decagon.

Solution

“Octa” in the octagon means “eight”. So, an octagon has eight sides. The formula for the number of diagonals is:

No. of Diagonals = n = p(p – 3)/ 2

Putting p = 8 in the above equation gives:

No. of Diagonals = n = 8(8 – 3)/ 2

n = 8(5)/2

n = 40/2

n = 20

Hence, the number of diagonals in an octagon will be twenty.

A decagon has ten sides as “deca” means “ten”, so p = 10. The number of diagonals will be:

No. of Diagonals = n = 10(10 – 3)/ 2

n = 10(7)/2

n = 70/2

n = 35

So, thirty-five diagonals can be drawn in a decagon.

Example 2

A rectangle has a length and width of 18 cm and 9 cm. What is the length of the diagonal in this rectangle?

Solution

The formula to calculate the diagonal’s length in a rectangle is given by:

Length of Diagonal = d = $\sqrt{ r^2 + s^2 }$

Where r is the length and s is the width or breadth. The values of r and s for this rectangle will be:

r = 18 cm , s = 9 cm

Putting the values in the equation gives:

Length of Diagonal = d = $\sqrt{ {18}^2 + {9}^2 }$

d = $\sqrt{ 324 + 81 }$

d = $\sqrt{ 405 }$

d = 20.1 cm

So, the length of the diagonal of the rectangle will be 20.1 cm.

All the images are created using GeoGebra.

Deviation Definition < Glossary Index > Diagram Definition