JUMP TO TOPIC
Difference|Definition & Meaning
Definition
In mathematics, a difference is the consequence of one of the most significant arithmetic computations, which seems to be gained by subtracting two numbers. It indicates how much one number differs from another. In math, the goal of determining the difference is to determine how many numbers lie between two given figures. The difference has symbols negative (-).
The first digit in the equation is the minuend. The next or second digit in the equation is subtrahend, and the result is the difference between two digits or two numbers.

Figure 1 – Difference Dictionary
Here in the above figure, as clearly mentioned, 9 is the minuend, 2 is the subtrahend, and 7 is the difference. So when we subtract 2 from 9, the result will be 7. Likewise, when we subtract 2 from 8, the result will be 2, and when we find the difference between 7 and 2, the result will be 5.
Various Procedures for Evaluating the Difference
Difference Between the Numbers Using Number Line
The numbers are also subtracted by a number line, and it is extremely useful for quickly determining the difference between two smaller numbers. We move to the left side of a number line while calculating the difference between two numbers on a number line. We begin with minuend and work our way down to the number towards the subtrahend. As a result of this, we will find the difference between the two numbers.
One such problem is handled in Example 1.
Difference Without Borrowing
To find the difference between the two numbers, the first and main step is to put the bigger number on the top, and the smaller number should be written below. We will start subtraction from the right side.
This sort of problem is dealt with in Example 2.
Difference With Borrowing
The borrow concept is applicable where the digits in the upper number are smaller than the lower number. If the number is less in ones place then we need to borrow one from the next place value, which is tens. If the number is less in the tens place value, one will be borrowed from the next place value, which is hundreds, and so on.
The process is detailed in Example 3.
Difference Between Decimals
The method of difference is the same as the usual whole numbers, but here we additionally have decimal points. The numbers before the decimal points are whole numbers, and the numbers which are after the decimal point are the fractional part.
We solve one such problem in Example 4.
Difference Between Fractions
The difference between the fractions is different from the difference between whole numbers and decimals. In fractions, there is a numerator as well as a denominator, so the method of difference is also changed for it. There are different cases to find the difference between the fractions. For every case, there is a rule to solve the difference.
- Check whether the fraction is like or unlike. If the fraction is like means the same denominator, we will simply subtract the numerator.
- When the fractions are unlike, we will take the LCM of the denominator or make the denominator the same, then simply subtract the numerator.
Example 5 deals with the difference between two pairs of fractions (one like and one unlike pair).
Solved Examples Corresponding to the Above Scenarios
Example 1
Find the difference between 5 and 0 using a number line.
Solution
The number line below shows the difference between 5 and 0.
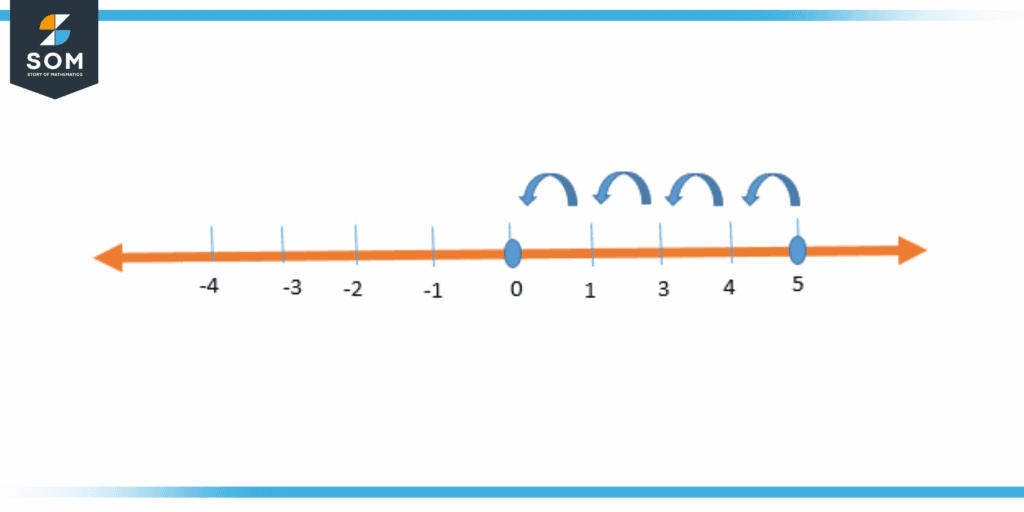
Figure 2 – Difference of Numbers using Number Line
In the above figure, we have to find the difference between two numbers that is 5 and 0 so we will move backward on the number line for subtraction, now here we will move four steps backward until we reach 0, so here:
5 – 0 = 5
The answer to the subtraction through the number line is 5.
Example 2
Find the difference between 7658 and 4237.
Solution
The figure here represents the difference between the two numbers, but the first number is greater than the other number. Like 7658 is greater than 4237, so in this case, we do not have to borrow.

Figure 3 – Difference without borrow
Here in the above figure, the ones place value is 8, which is bigger than the lower number’s ones place value of 7, so there is no need to borrow. This is the case for all digits here. Thus, when 4237 is subtracted from 7658, the answer will be 3421.
If the ones place value of the upper number is smaller than the lower number then we have to borrow 1 from the tens place value of the upper number (next example).
Example 3
Solution
This is an example of the difference between borrow and carrying. The ones place value in the first number is 6, and the ones place value of the second number is 7 means here 6 is smaller than 7, so we have to take carry or borrow one from the next place value.

Figure 4 – Difference with borrowing.
Here in the figure above, the ones place value of the upper value is less than the ones place value of the lower number. We need to make the number in the upper number’s ones digit bigger than the lower number’s ones digit because a smaller digit can not be subtracted from a bigger one.
Here, 1 is borrowed from the tens place value, which makes the ones place become 16, and the tens place is one less, which is 4. Further, the subtraction now follows the casual rule.
Example 4
Solution
The difference between decimals is the same as whole numbers.
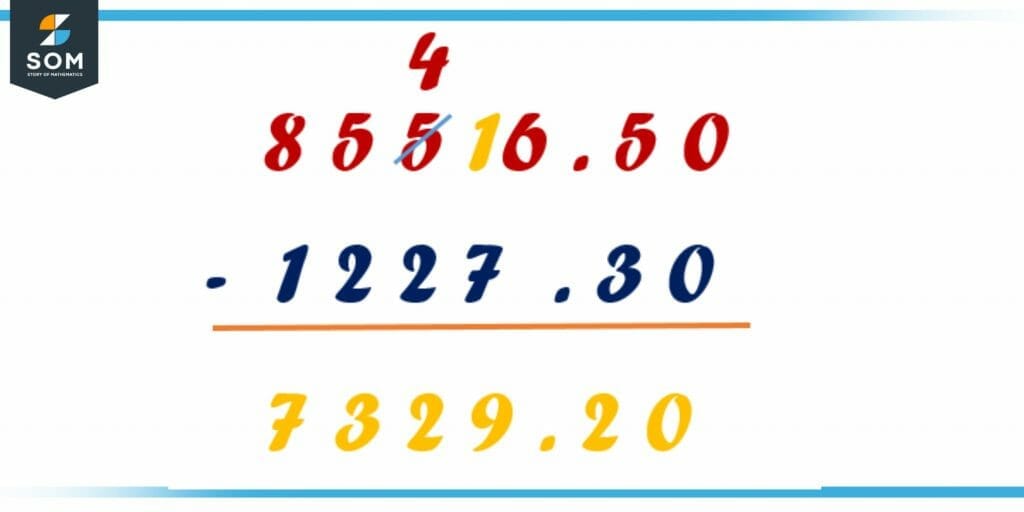
Figure 5 – Difference of decimal numbers
Here in the figure, the right-hand side numbers are whole numbers, whereas the left-hand side numbers of the decimal points are the fractional part. In the above figure, 8556 is the whole number, whereas 50 is the fractional part. In the other decimal number, 1227 is the whole number, and 30 is the fractional part. The subtraction of decimal numbers follows the same rule as simple whole numbers.
Example 5
Find the difference between 9/5 and 3/5 and also the difference between 8/7 and 3/5?
Solution
Here 9/5 and 3/5 are two like fractions. So, we will take the difference of numerator.
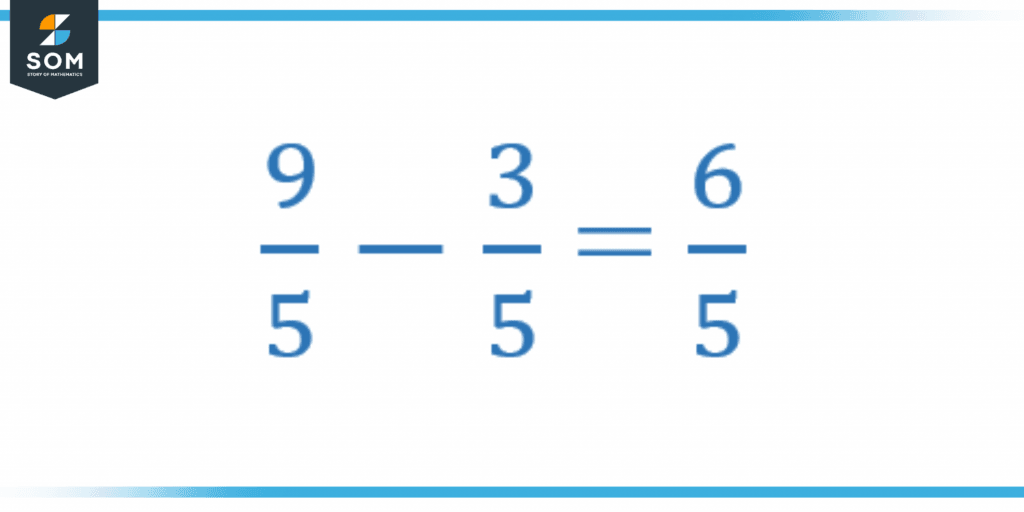
Figure 5 – Difference of like fractions
The above figure shows the difference between the two like fractions because the denominator is the same. In this case, the numerator will be simply subtracted like 9/5 – 3/5 = 6/5
In the next figure, the subtraction is between two unlike fractions; the numerators and denominators of both fractions are different! In this case, we have to convert unlike fractions to like fractions. To do that, we can take LCM, or another method is to make both the denominator same by multiplying and dividing one or both of the fractions with a certain number. After converting the fractions into like fractions, we can simply use the previous method (subtract numerators).
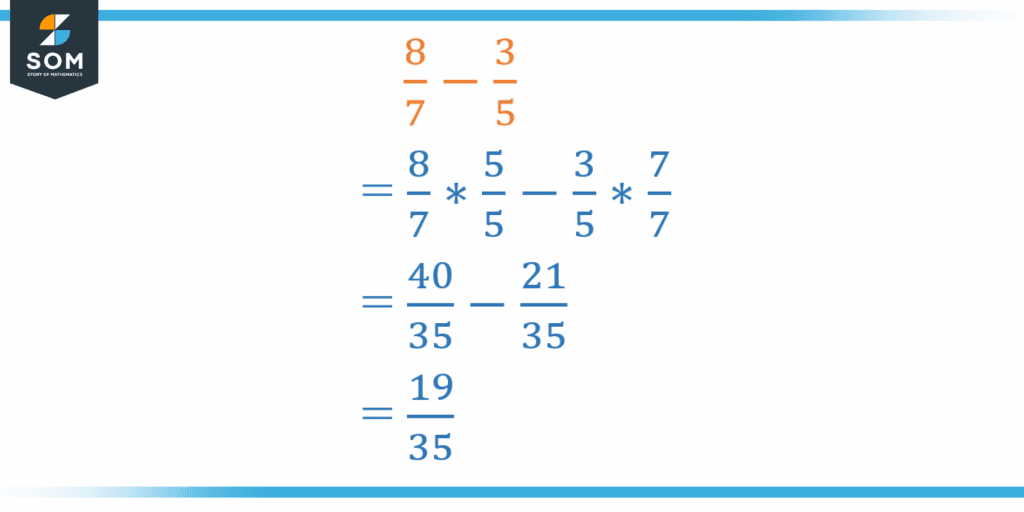
Figure 6 – Difference of unlike fractions
All figures above are created on Geogebra.
