JUMP TO TOPIC
Dimension|Definition & Meaning
Definition
Dimension is the measure of the length of an object in one direction. In mathematics, it elaborates the idea that line is one-dimensional, the plane is two-dimensional and space is three-dimensional. These dimensions are extensively used in geometry.
For an object, its topological measure of size is recognized as dimension. To specify the position of an object or point on a plane or in space, the number of coordinates needed is actually the number of dimensions of the object.
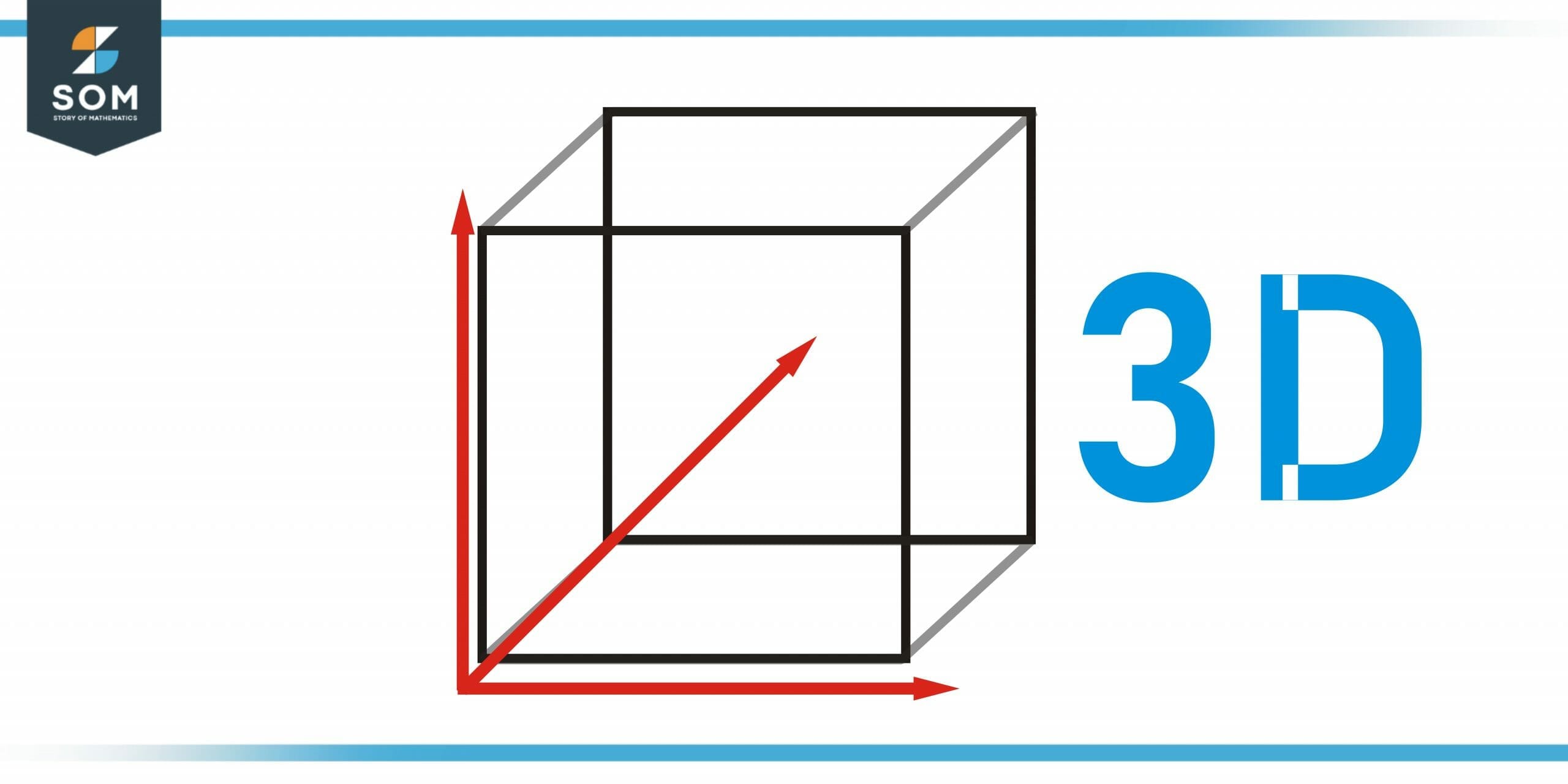
Figure 1 – Cube is a three-dimensional object
Let’s take a few examples of some objects, a rectangle drawn on paper has two lengths that are length and widths, so it is two-dimensional. To measure a cube you need three coordinates i.e length, breadth, and height, so it is a three-dimensional object. The term ‘dimensionality’ is also used for the dimension of objects.
Images Representing Different Dimensions
The objects we see around us are zero-dimensional, one-dimensional, two-dimensional, or three-dimensional. In the following paragraphs, you will understand the difference between these dimensions and their basic properties along with the images.
Zero Dimensional
An object without any length, height, or width is known as zero dimensional object. A point is considered a zero-dimensional object. It has no measurable lengths, it only indicates some location on a plane. It is also sometimes called a dimensionless object.

Figure 2 – A point on paper is a dimensionless object
One Dimensional
An object which has only one measurable side or length is known as a one-dimensional object or figure. The line is an example of a one-dimensional figure or object. A line has only one measure able part, that is its length. It has no width. A line segment can be a straight line or curved.
Two Dimensional
An object with two measurable sizes on flat surfaces or planes is known as a two-dimensional image or object. Such figures are measurable along only two sides and they have no thickness i.e third dimension in their shape.
In our paper works, we usually deal with two-dimensional figures or images. Most of the basic geometrical shapes are two-dimensional in nature. For example, triangles, rectangles, circles, parallelograms, rhombi, squares,s, etc are all two-dimensional figures and we extensively use them in mathematics.
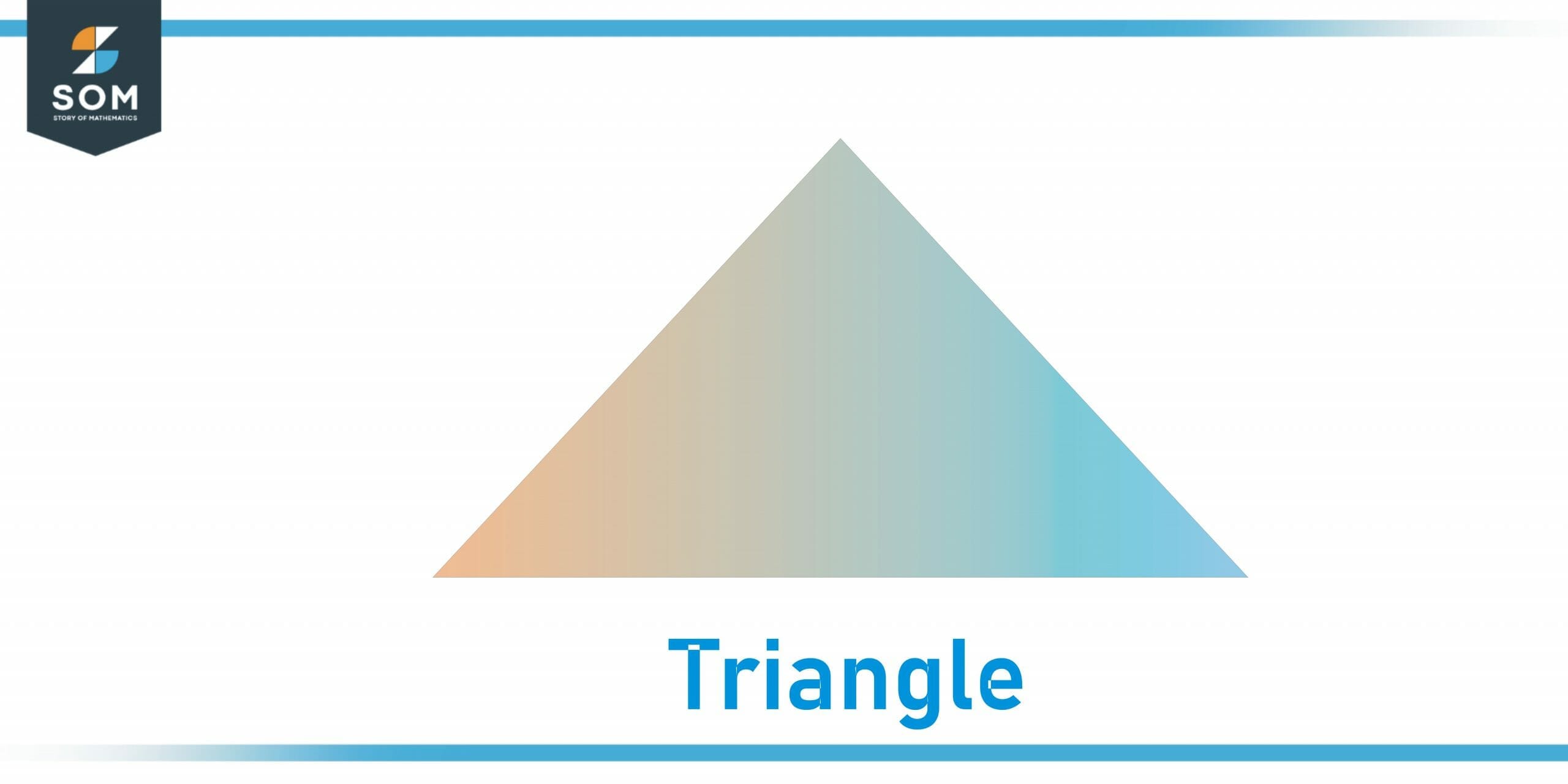
Figure 3 – A triangle is a two-dimensional figure
Another very common system we use in mathematics is the x-y coordinate system. This is a two-dimensional system that we mostly use. The x and y axis are perpendicular to each other. This system is used to plot two-dimensional figures.
Three Dimensional
An object with three solid measurable sides or sizes is known as a three-dimensional object figure or shape. The objects we see around us in real life are mostly three-dimensional in nature.
A three-dimensional figure must have three measurable faces length, width, and height. Their thickness along with length and height makes them different from two-dimensional objects or figures.
A Cube is the most basic example of a three-dimensional shape. It has three dimensions i.e length, breadth, and height. It has a face, vertex, and edges. On paper, three-dimensional shapes are drawn on a 3D cartesian plane. It has an x-axis, a y-axis, and a z-axis. All three axis are perpendicular to each other.
What is Four-dimensional Space?
Mathematics has been advancing with new developments in science, especially in physics. This advancement led to introduce another dimension which is the fourth dimension. It is not much popular among ordinary people, but scientists are working on it.
The fourth dimension is the advanced extension of a three-dimensional object. It is a complex concept that is still developing. Some scientists consider time the fourth dimension and represent it in a complex animation model.
Dimension as Measurement
If the length is measured in one direction it is also known as its dimension. In simple words, we can say that the unidirectional measurement of length is the dimension of that object. The number that shows the size or amount is known as measurement. Two systems are used for measurement i.e. metric and US standard.
Dimension of Our World
Each and everything that our eye can see is three-dimensional. This can be from a piece of paper to a large building in any city. All these objects are three-dimensional. If we closely see a paper under a microscope, we will realize that it also has some width.
There are certain diagrams that we draw on paper to represent them as two-dimensional. For example, a square is drawn on paper. We call it two-dimensional in our minds. These drawings are our mental pictures on paper to understand and think about them.
Importance of Dimension
- Dimension is an important parameter in both mathematics and physics. For geometric objects, the concept of dimension gives precise readings of the complexity and its conceptual or visual elements.
- Dimension of the objects helps to know the quantity, shape, and size of objects.
- The trade done all over the world is dependent on standard dimensions. If there were no standard dimensions, trade could not be possible.
- All the structured products are dependent on dimensions, if dimensions are not kept in focus, structures would not work.
- The study of dimension is also important in particle physics and astronomy.
Some Examples of Three-Dimensional Shapes
a) What are the dimensions of the curved line given in the figure below?
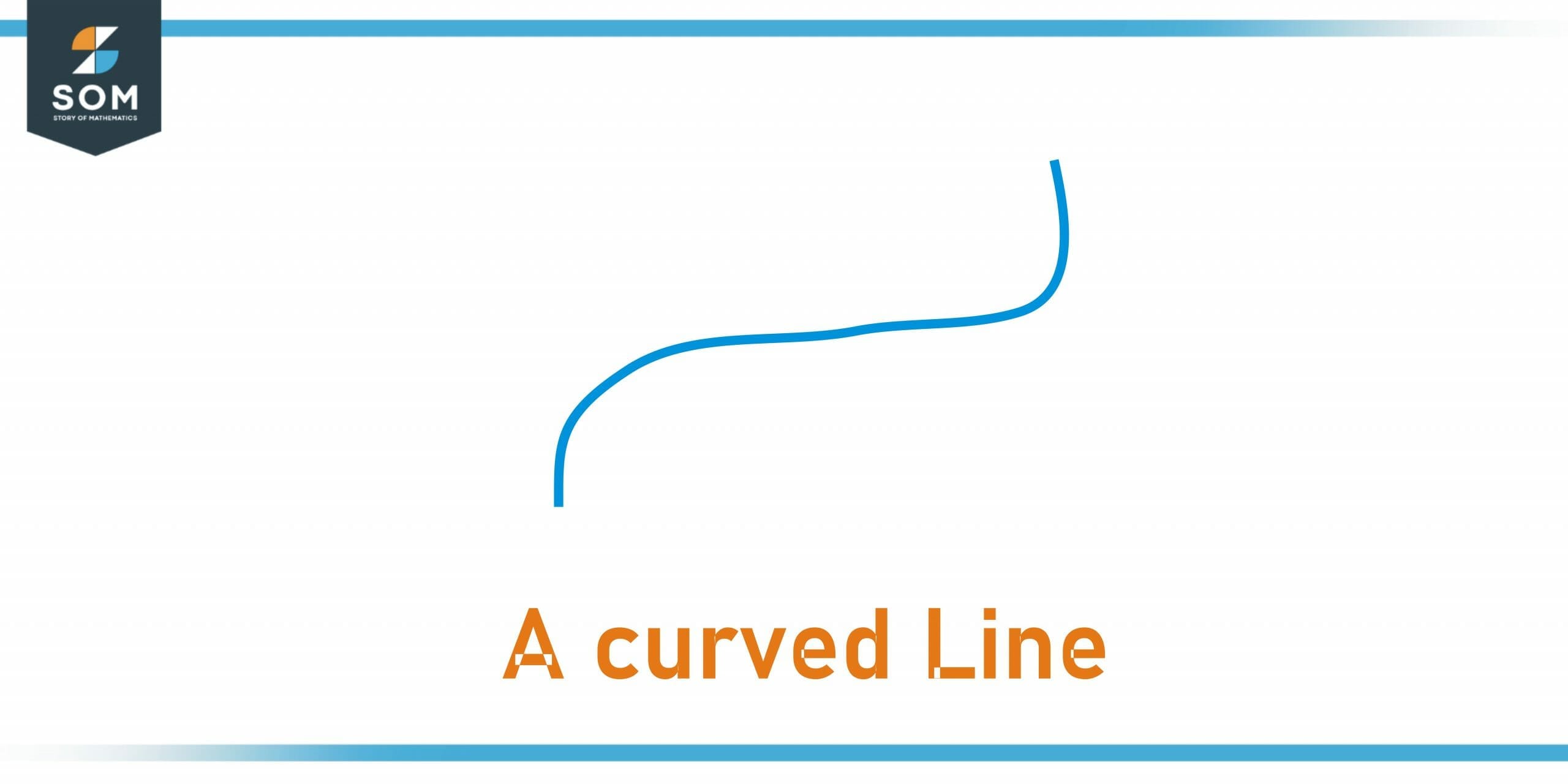
Figure 4 – A curved line
b) Can you figure out the dimensions of the point given in Figure 5?

Figure 5 – A geometrical point.
c) You use the ruler to draw straight lines. How many dimensions does a ruler have?

Figure 6 – A ruler used to measure small lengths
d) The cube in Figure 1 has six sides in it. Is it two or three-dimensional?
e) How many dimensions does a closed laptop have?
Solution
a) The given figure is a curved line. We can see that we can only measure its length. So, it has one dimension.
b) This figure just has a point in it. We know that point has no length, width or height so, it has no dimension or we can say that it’s dimension.
c) A ruler has length and breadth that we can easily measure but its thickness can also be measured with precise instruments. So, it is a three-dimensional object.
d) The cube has six sides but it has a length, a breadth, and a height in it which clears that it has three dimensions.
e) It is also a three-dimensional object.
All mathematical images are generated on GeoGebra.
