Directed Number | Definition & Meaning

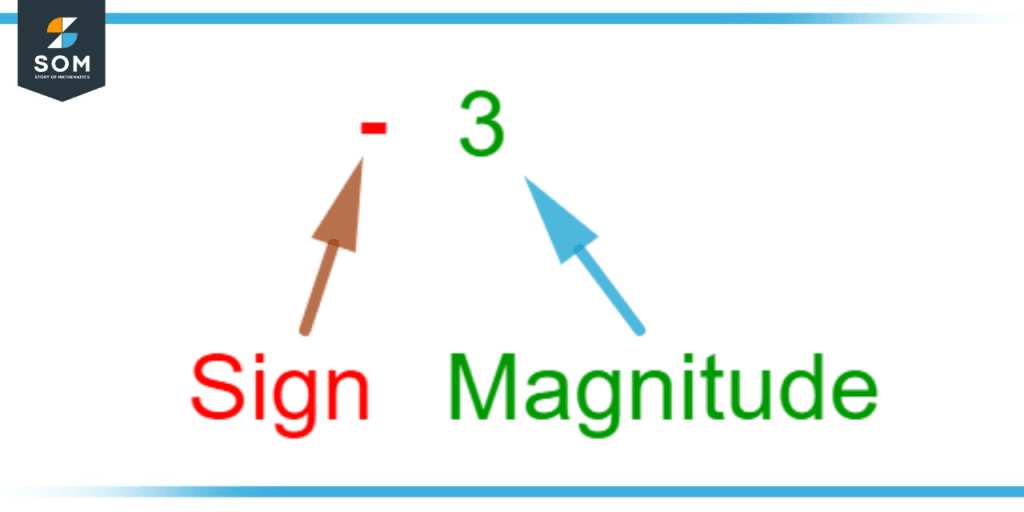
Figure 1 – Notation used for directed numbers.

Operations 

The operations for directed numbers are influenced by the sign of the number. The basic arithmetic operations for directed numbers are discussed below.

Addition

The addition of directed numbers where both the operands have the positive sign is equivalent to the simple addition of numbers. In such a case, the result is always positive, and the magnitude of the sum is greater (both operands greater than zero) or equal to one of the operands (one of the operands is zero). 

In the case where both the numbers differ in sign, i.e., one operand is positive, and the other is negative, the resultant sum will have the sign of the number which is greater in magnitude. The magnitude of the resultant will be obtained by subtracting the magnitude of both operands. The magnitude of the sum, in this case, will be in between the magnitude of the operands, i.e., it will be smaller than the magnitude of the higher magnitude number but greater than the magnitude of the lower magnitude number. 

When both operands have a negative sign, the sum will also have a negative sign, with the magnitude of the sum equal to the sum of the magnitudes of the individual operands. Thus, this is similar to the case of both operands being positive numbers. 

For numbers that have more than a single digit, their addition is usually done by a method called column addition. The numbers are stacked vertically such that the digits in unit’ position are over each other and so on. Then the numbers are added vertically starting from right most digit and moving leftward. If a sum of two digits numbers is produced, the number at tenth place is carried over to next addition on the left and added. This is illustrated with an example below.

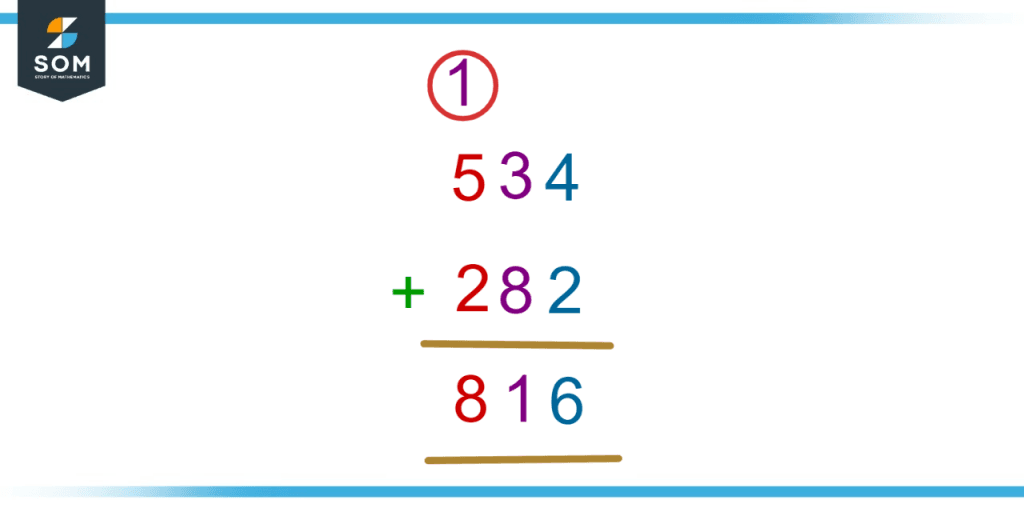
Figure 2 – Example of column addition of multi-digit numbers.

Subtraction

The subtraction of directed numbers works in a similar way to the addition, except that there is an additional negative sign introduced by the operation of subtraction itself. This additional negative sign can be made part of the second operand to produce a form equivalent to that of the addition of the numbers. 

For two numbers a and b, their difference is expressed as:

a – b

Since the multiplication of a positive and a negative sign produces a negative sign, the negative sign for subtraction can be factored into a product of the positive and negative sign to produce:

a + (-b)

This expression is the same as the addition of a and -b, and so the subtraction can be viewed as the addition of the first operand and the negative of the second operand. The negative sign with b just indicates that the sign of the second operand is changed from its original state. Thus, for the case that b is a negative number, -b will be a positive number and vice versa. 

Note that the sign is changed for the second operand only, and changing the sign of the first operand will not have the same effect. This is because the commutative property does not hold for the subtraction of numbers and so a – b is not equal to b – a.  

Multiplication

The multiplication of directed numbers is rather simple – the magnitude of both the operands gets multiplied, and the signs also get multiplied with each other. The four cases of signs of the operands and the sign of the operands are shown in the table. 

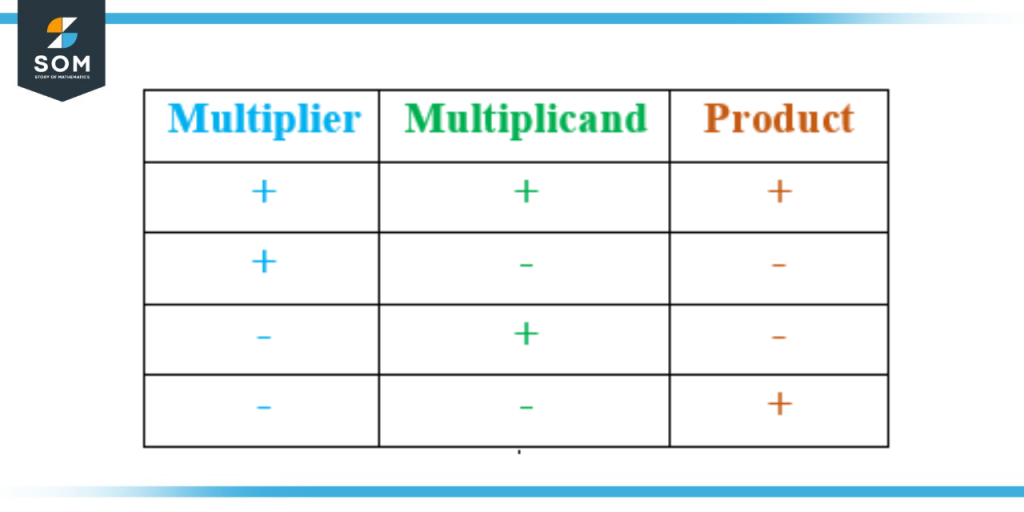
Figure 3 – Relation between signs of product and operands for multiplication.

It can be seen that when both operands have the same sign, the sign of the product is always positive. For the case when the operands have opposite signs – irrespective of the order of operands – the sign of the product will always be negative. 

The same concept can be extended to the multiplication of more than two numbers. For the product of three numbers, first, multiply the two operands using the sign conventions above, producing a partial product. Treat this partial product as one operand and the third operand as the second operand and perform the procedure of multiplication of two operands again. 

Division

Division of the directed numbers works in the same way as multiplication, except that the magnitude of the operands gets divided rather than multiplied. The sign of the result is the same as in the case of multiplication. Thus, the division of two directed numbers with the same sign will always produce a positive quotient, and the division of oppositely signed divisor and the dividend will produce a negative quotient. 

Example of Operations With Directed Numbers

John runs a small business in which he buys several items at a wholesale rate and then sells them individually. Consider his business transactions for the last week. He bought the items for $85. There were a total of 8 items, and he managed to sell them for a price of $13 per item. Compute the net profit earned by John during the week. 

Solution

It is required to compute the net profit earned by John from his business. The net profit of a business determines the amount that is actually earned by the business owner after taking care of the costs of the business from the sales. 

For the given case, the cost is the price of buying the items in the first place. The cost is given as $85. Since the cost can be considered as a loss (opposite of profit), the cost can be represented as a -$85 balance for the business owner. 

John sold each of the eight items for a price of $13. The total sales for John will be the total price obtained from selling all the items. This can be obtained as:

13 + 13 + 13 + 13 + 13 + 13 + 13 + 13

The same repeated addition can also be represented as multiplication by using the definition of multiplication:

13 x 8

This product results in $104. Now, since this represents profit for John, it can also be represented as +$104. 

The net profit for John will be the sum of the negative profit from the cost of items – or the loss – and the total money obtained from selling the items. This can be expressed as:

-$85 + $104 

As discussed earlier, for the case when one of the operands has a positive sign, and the other has a negative sign, the magnitudes of the operands are subtracted. This produces:

$19

And the sign of the result is the sign of the operand with the higher magnitude. Here, the magnitude of +104 is higher than the magnitude of -85, so the sign of the result will be positive. Hence, the net profit is:

+$19

All mathematical drawings and images were created with GeoGebra.

Dimension Definition < Glossary Index > Discount Definition