Discount|Definition & Meaning

The term discount is very common and we are all familiar with the concept when it comes to the shopping perspective. Mathematically, its just a reduction in price specified in the form of some absolute cash price or in terms of percentage. Following figure represents a photo shows a sample discount offer typically published by vendors and stores all over the world. 

Figure 1: Introduction to Discount

Explanation of Discount

In mathematics, discount is a percentage or fractional value that characterizes reduction in the price of a product or service. Consider the example of a bicycle. Lets say that the list price of the bicycle was 800 united states dollars. Now the store owner wants to increase the cash flow to accommodate new line of bicycles. To achieve this he or she offers a discount of twenty percent.

Figure 2: Bicycle Example of Discount

The twenty percent of the list price of the bicycle is 800 x 20 / 100 = 160. Hence, the new price after the deduction of discount, can easily be calculated by using simple subtraction 800 – 160 = 640 united states dollars.

Mathematical Formula for Discount

In the above example new price and the discount was calculated using some intuition. In this section, we formally introduce the mathematical form of the discount calculations. Lets assume that the original price of a given product or service is symbolized by ‘O’. The new price of the same product or service after discount is symbolized by ‘N’. And the discount rate in percentage terms is symbolized by ‘d’.

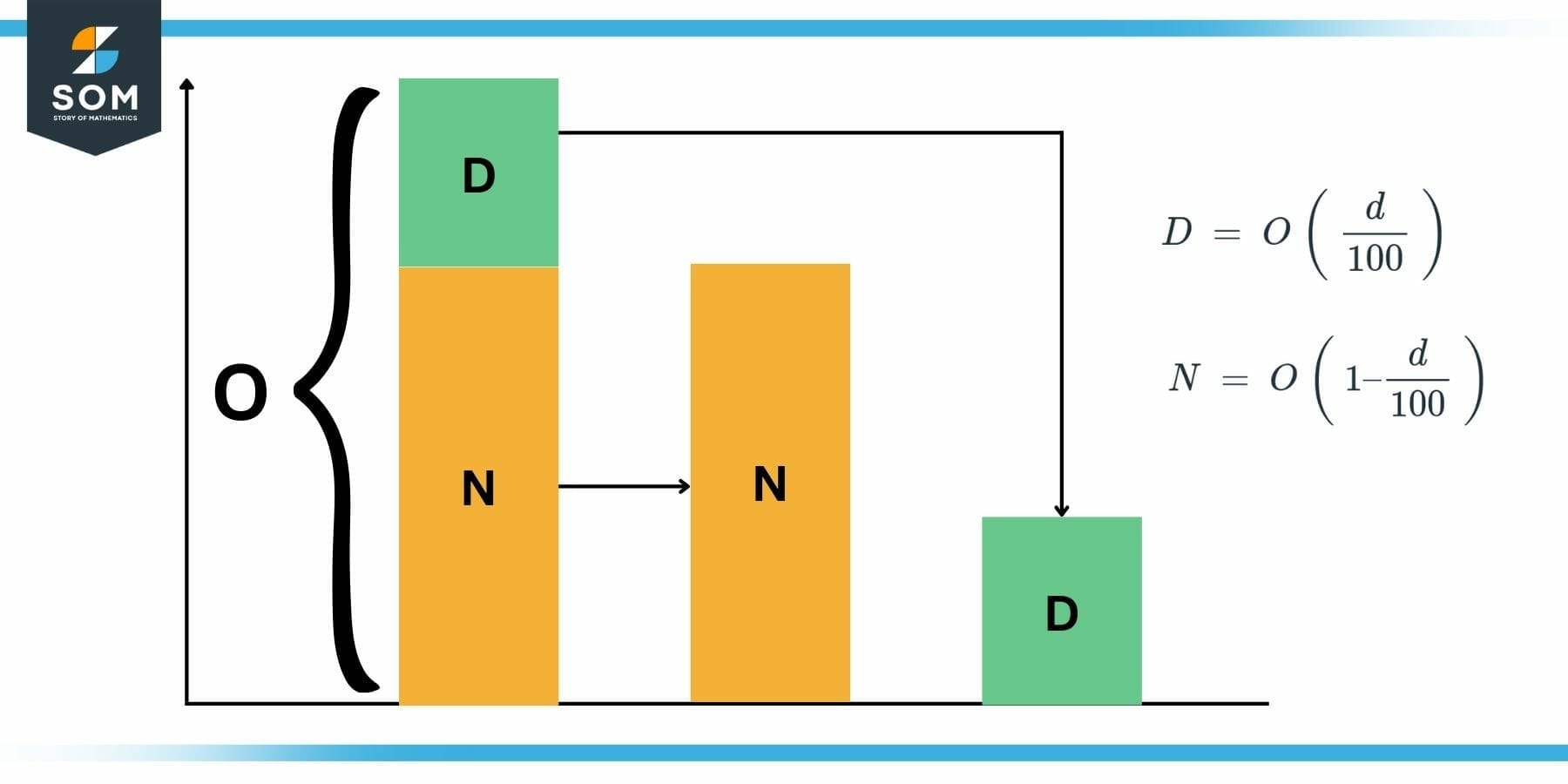
Figure 3: Mathematical Form of Discount and New Price

Under these abstractions, we can write the following formula:

N = O$\mathsf{\left(1-\dfrac{d}{100}\right)}$

The discounted or saved amount ‘D’ can be calculated by using the following formula:

Discount Amount = D = O$\mathsf{\left(\dfrac{ d }{ 100 }\right)}$

Applications of Discount

There are many examples of discount that we may see in daily life where we may have to calculate the new price after the discounted amount. We may have to make decisions about whether or not to buy a certain product. You may have to compare two or more products with  each other while adjusting the discounts for some or all of them.

Suppose you wanted to buy a house for the family. Last week you checked a beautiful house worth eighty thousand united states dollars. At that time you couldn’t afford it since your budget was seventy thousand united states dollars. Now you receive an offer from your real estate dealer that the house owner is willing to give a 15 percent discount if the buyer pays in cash.

To see whether or not the house is in your range, you may use the formulae given above to find the new price of the house as follows:

N = \$80,000$\mathsf{\left(1-\dfrac{ 15 }{ 100 }\right)}$ = \$68,000

Now that you know that the new price would be sixty eight thousand united states dollars which is within your budget of seventy thousand, you can easily make a decision and confirm you order to the dealer.

Figure 4: Example of Discount on a New House

Other Uses Cases of the Term Discount

The term discount may have different meaning in different areas of mathematics. Following are some of the use cases in the field of business mathematics or the mathematics of economics.

Discount Loan

In any loan agreement, the lender and borrower reach an agreement to how the interest amount and the principle amount will be paid over the whole tenure. Sometimes, the lender decides to deduct the interest amount in first few installments while maintaining the principle amount at a stand still. The type of loan where the interest payment is deducted mostly in first few installments is called discount loan.

Discount Rate

The discount rate is a term often used synonymous to the term interest rate. More formally, the discount rate is the interest rate declared by the central bank or any central authority responsible for making the fiscal policy of a country. This discount rate is used as a reference interest rate for rolling out discount offers and money borrowing packages of the commercial banks.

Numerical Examples of Discounts

Example 1

The listed price of a sports car is ninety thousand dollars. You have heard that the car manufacturer has announced a discount of 25% for the 100% upfront payment on Christmas. What would be the discount amount and the new price of the car?

Solution

Given:

d = 25%

O = 90,000 USD

Calculating the discount amount:

D = O $\mathsf{\left( \dfrac{ d }{ 100 }\right)}$

D = 90,000 USD $\mathsf{\left(\dfrac{ 25 }{ 100 } \right)}$

D = 90,000 USD ( 0.25 )

D = 22,500 USD

Calculating the new price:

N = O $\mathsf{\left(1-\dfrac{ d }{ 100 }\right)}$

N = 90,000 USD $\mathsf{\left(1-\dfrac{ 25 }{ 100 } \right)}$

N = 90,000 USD ( 0.75 )

N = 67,500 USD

Example 2

Suppose that you want to visit Turkey for the term break. The price of the seven day tour of a single individual is two thousand dollars. The travel company has a package for group tours. Under this package, if you book the travel plan as a group of four people, you get a discount of fifteen percent. What will be the value of discount amount in dollars. What will be the revised rate after the discount for a single individual.

Solution

Given:

d = 15 %

O = 2,000 USD

Calculating the discount amount:

D = O $\mathsf{\left(\dfrac{ d }{ 100 }\right)}$

D = 2,000 USD $\mathsf{\left(\dfrac{ 15 }{ 100 }\right)}$

D = 2,000 USD ( 0.15 )

D = 300 USD

Calculating the new price:

N = O $\mathsf{\left(1-\dfrac{ d }{ 100 }\right)}$

N = 2,000 USD $\mathsf{\left(1-\dfrac{ 15 }{ 100 }\right)}$

N = 2,000 USD ( 0.85 )

N = 1,700 USD

All images were created with GeoGebra.

Directed Number Definition < Glossary Index > Discrete Data Definition