JUMP TO TOPIC
Distributive Law|Definition & Meaning
Definition
According to the Distributive Law in mathematics, carrying out one multiplication at a time is equivalent to multiplying a value by a collection of previously added numbers. For instance: [4× (3 + 4)] = (4 × 2) + (4 × 4).
What Is the Distributive Law
A single value, along with two or more values contained within a set of parentheses, can be multiplied with one another using an algebraic property known as the Distributive Law.
According to the Distributive Law, to correctly calculate the result of multiplying a factor by the sum or addition of two terms, it is necessary first to perform multiplication on each of the two numbers by the factor and then to carry out the addition operation.
This is because the factor is multiplied by the sum or addition of both numbers. The following is a symbolic representation of this property:
X (Y + Z) = XY + XZ
Where X, Y, and Z each correspond to a different value.
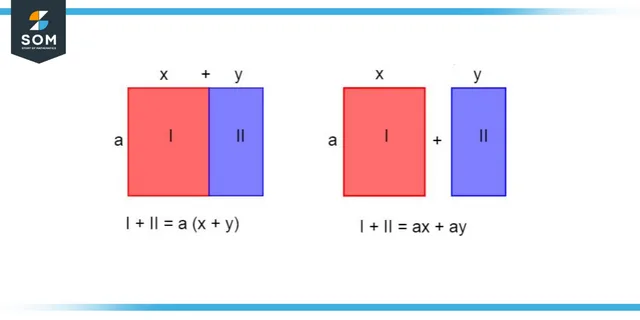
Figure 1: Distributive Law of Multiplication
Distributive Property With Variables
Take a look at the following example: 7 (3 + 5x)
Because the two numbers contained within the parentheses can never be added together because they do not correspond to the same thing, the problem cannot be simplified anymore. We need an alternative way, and Distributive Property can be employed in this situation as an option.
When the Distributive Property is considered:
(7 × 3) + (7 × 5x)
The parenthesis has been eliminated, and each phrase has been increased by a factor of 6.
You should now be able to simplify the multiplication by only considering individual terms.
21 + 35x
Expressions that involve multiplying a number by a sum or difference can be made more straightforward by utilizing the distributive property of multiplication. This property states that the product of the sum or difference of a number is equivalent to the sum or difference of the multiplication of the number. In algebra, the distributive property can be used for two different arithmetic operations, such as the following:
- Distributive Law in Multiplication
- Distributive Law in Division
The Distributive Law in Multiplication
One way to describe the distributive property of multiplication is by using addition and subtraction operations. That indicates that the operation is carried out within the brackets, specifically, the addition or subtraction that occurs between the integers within the brackets. Let’s understand these features better by looking at some examples.
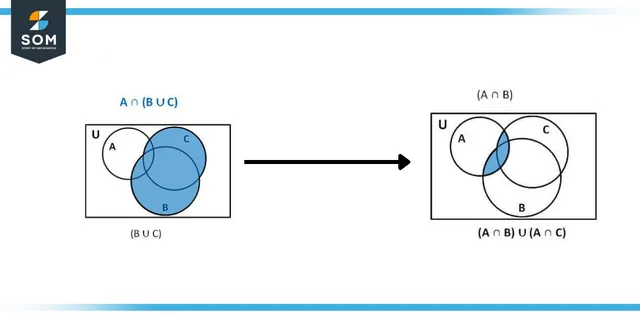
Figure 2: Venn Diagram of Distributive Law
The Distributive Law of Multiplication Over Addition
When you multiply a value, you use the distributive property of multiplication, which is an advantage that multiplication has over addition. As an illustration, you need to multiply 6 by the total of 5 and 3.
Because these are related terms, we typically begin by adding the numbers together and then proceed to multiply by 6:
6(5 + 3) = 6(8) = 48
However, to fulfill the requirements of the property, you must first multiply each addend by 6. After completing this step, which is known as dispersing the 6, you may add the products.
Before you proceed with the addition, we will first perform the multiplication by multiplying 6(5) by 6(3):
6(5) + 6(3) = 30 + 18 = 48
You’ll notice that the outcome is precisely the same as it was. You probably need to know that you are employing it in any given situation.
Both approaches are modeled by the equations that are presented below. On the left-hand side, we have the numbers 5 and 3, which are then multiplied by 6. This expansion is rewritten by applying the distributive law on the right-hand side, where we distribute 6, multiply by 6, and then sum the results.
You will observe that the outcome is comparable in each of the three scenarios. The new form is as follows:
6(5 + 3) = 6(5) + 6(3)
6(8) = 30 + 18
48 = 48
Distribution Law of Multiplication Over Subtraction
Let’s look at an illustration of multiplication’s distributive property over the arithmetic of subtraction.
So, let’s say we need to divide 8 and 5 from a product of 6.
There are two methods for achieving this result.
Case 1: 6 × (8 – 5) = 6 × 3 = 18
Case 2: 6 × (8 – 5) = (6 × 8) – (6 × 5) = 48 – 35 = 18
Whichever method is used; the outcome will be the same.
Expressions can be rewritten using the distributive properties of addition and subtraction. Using addition and multiplication is acceptable when multiplying by a sum. Another option is to multiply each addend separately and then add the resulting results. This also holds for subtractions. Multiplication occurs with each number inside the parenthesis before any addition or subtraction is performed because the outer multiplier is shifted in each case.
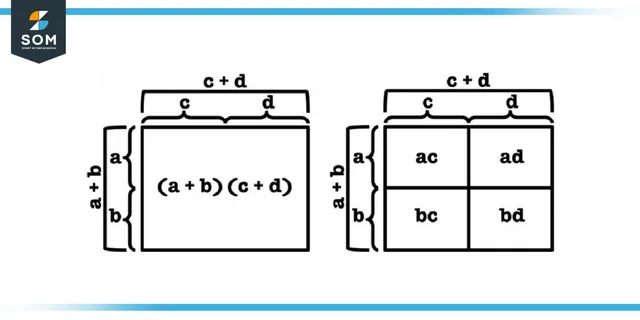
Figure 3: Tabular Form of Distributive Law
What Is “The Distributive Law of Integers”?
Integers have a feature known as the distributive property, which states that the product of an integer multiplied by the sum of two integers contained inside parenthesis is equivalent to the sum of the individual products of integers. Assuming that a, b, and c are all whole numbers, we may express the distributive property of multiplying integers by writing it as [a (b + c)] = ab + bc. This is because integers’ multiplication takes precedence over integers’ addition.
Examples of the Distributive Law in Action
Example 1
A dozen pencils cost \$3; a dozen pens cost \$5. Write an expression for purchasing four pencils and pens w.r.t the cost. Moreover, find the total cost using the distributive property.
Solution
The expression representing the pen and pencil cost:
4 x (Addition of cost of both the pencil and pen)
= 4 x (3 + 5)
The total cost becomes:
= (4 x 3) + (4 x 5)
= $32
Example 2
There are two boys and three girls in each row of a class, with a total of four rows. Find the total number of students in the class, considering the distributive property.
Solution
The expression representing the boys and girls in four rows:
4 x (Addition of cost of both the girls and boys in each row)
= 4 x (2 + 3)
The total students:
= (4 x 2) + (4 x 3)
= 20 Students
All mathematical drawings and images were created with GeoGebra.
