JUMP TO TOPIC
Diverge|Definition & Meaning
Definition
The divergent sequence is the one in which the words never come close to zero. they persist to raise or decline and they loom infinity as n comes infinity.
Diverge (in the context of sequences and series) means not settling towards some value. In other words, not converging to a fixed value. When a series (sum of all elements in a sequence) diverges, it goes to positive or negative infinity as the number of elements in the sequence approaches infinity.
Figure 1 – Depiction of Diverge
The particular phrases of the series must verge zero if a series converges. Therefore any series in which the respective representations do not approach zero, subsequently diverge. Regardless, convergence is a more powerful condition. There is a possibility that not all series whose terms approach zero converge. A harmonic series is a very suitable example.
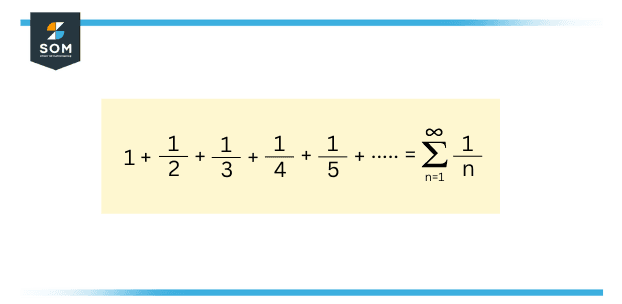
Figure 2 – Harmonic Series
Nicole Oresme, a medieval mathematician, proved the divergence of the harmonic series
Infinite Series
Any ordered infinite sequence as in current nomenclature, $(a_1 , a_2 , a_3 ,\space … )$ of representations (that is functions, numbers, or anything that can be counted) explains a series, which is the operation of summing the $a_i$ one after the other. Because of the fact that there are an infinite number of terms in the series, it is called an Infinite Series. Infinite series is described(or characterized) with an expression like:

Figure 3 – Infinite Series
The infinite sequence of additions that are denoted by a series cannot be virtually taken on (at the smallest in a finite portion of time). Nevertheless, it is occasionally attainable to transfer a value to a series if the set from which the numbers and finite aggregates of numbers belong has an idea of limit, named the sum of the series.
This value is the boundary as n overlooks to infinity (if the limitation persists) of the addition of the $n$ first instances of the series, that are named the nth partial sums of the series. That is described as:
\[ \sum_{i=1}^{\infty} = lim_{n \rightarrow \infty} \sum_{i=1}^{n} a_i \]
One states that the series is convergent or summable if this limit persists, or if the arrangement $(a_1, a_2, a_3, … )$ is summable. In this matter, the limit is named as the sum of the series. If that’s not the case, the series is said to be divergent.
The following notation $\sum_{i=1}^{\infty} a_i $ characterizes both the series, that is the implied method of summing the terms of the series indefinitely. if the series converges, the outcome of the procedure is the sum of the series. This is a conception of the identical ritual of indicating by $a + b$ both the addition, and the process of adding, and its outcome is the sum of a and b.
Theorems on Methods for Summing Divergent Series
A summability procedure denoted as M is standard if it coordinates with the authentic limit on all convergent series. Such a derivative is anointed an Abelian theorem for M, derived from the prototypical Abel’s theorem. More subtle in nature, called Tauberian theorems, partial converse results from a prototype proved by Alfred Tauber.
Here, partial converse describes that if M sums the series $\sum$, and some side-condition maintains, then $\sum$ was convergent in the foremost position; without any side-condition, this type of outcome would state that M only added convergent series (making it worthless as an addition method for divergent series).
The operation providing the aggregate of a convergent series is linear, and it pursues from the Hahn–Banach theorem that it can be expanded to a summation process summing any series with fixed partial sums. This is known as the Banach limit.
This truth is not very helpful in training, as there are many such attachments, fluctuating with each other, requiring invoking the axiom of choice or its equivalents, and also proving such operators exist such as Zorn’s lemma. They are consequently not constructive in nature.
The topic of divergent series, as a discipline of mathematical computation, is mainly discussed with detailed and realistic procedures such as Abel summation, Cesàro summation, and Borel summation, and their relationships. The beginning of Wiener’s tauberian theorem sketched an approach to the subject, presenting unplanned associations to Banach algebra techniques in Fourier calculation.
Convergent vs. Divergent Series
A convergent series also called a limit, is a series whose partial sums lean to a distinctive number. A divergent series by difference is a series whose partial sums, don’t come to a limit. Divergent series traditionally go to $\infty$, go to $- \infty$, or don’t come to one specific number.
A simple example of a convergent series is as follows:
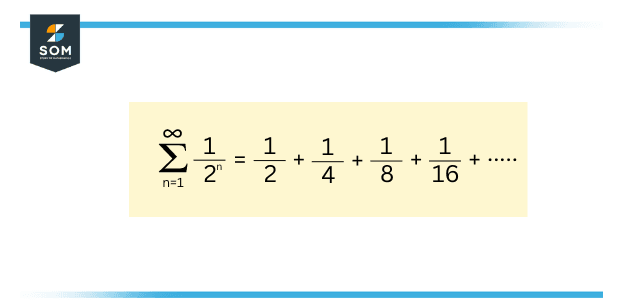
Figure 4 – Convergent Series
The Partial sums glimpse like this:
\[ \dfrac{1}{2}, \dfrac{3}{4}, \dfrac{7}{8}, \dfrac{15}{16}, \dots \]
and we can also notice that they reach nearer and nearer to 1. The foremost partial sum is $\dfrac{1}{2}$ away, the second $\dfrac{1}{4}$ away, and so on and so forth until it is infinitely near to 1. This means that the above series converges to a limit of 1.
The convergence of various series is a merely suitable issue in higher math and multiple important mathematical findings rotate around various series, but for the intentions of Algebra 2, we can specifically involve ourselves with that whether or not geometric series will converge.
Provided a geometric series with a standard ratio $r$, it will converge whenever $|r|<1$. If we had a geometric series with a common ratio of say, 2, this should create instinctive sense, we would have something that peeks like:
\[ \sum_{n=0}^{\infty} 2^n = 1+2+4 +8+16+ \dots \]
Indeed, the numbers we are adding to the sum get bigger and bigger, so the sum would never be restricted down and comes to a specific limit. Following is an example of a divergent series.
Again, if the common ratio is −2, the series:
\[ \sum_{n=0}^{\infty} (-2)^n = 1-2+4 -8+16-32+\dots. \]
will also diverge. A better way to see this is:
\[ \sum_{n=0}^{\infty} (-2)^n = (1-2)+ (4-8)+ (16-32) + \dots \]
\[ = -1 -4 -16 \]
\[ = – \sum_{n=0}^{\infty} 4^n \]
which is absolutely divergent.
An Example of Determining if a Series Diverges
Find out if the series given below is divergent or convergent.
\[ \sum_{n=1}^{\infty} n\]
Solution
To identify if the series is convergent, we are first instructed to use the formula:
\[ s_n = \sum_{i=1}^{n} i\]
The value of the series can be:
\[ s_n = \sum_{i=1}^{n} i = \dfrac{n(n+1)}{2}\]
So, to find out if the series is converging, we are preferably demanded to examine the arrangement of partial sums:
\[ \left. \frac{n(n+1)}{2} \right\rvert_{n=1}^{\infty} \]
\[ lim_{n \rightarrow \infty } \dfrac{n(n+1)}{2} = \infty \]
Accordingly, the sequence of partial sums diverges, and consequently, the series also diverges.
All images/mathematical drawings were created with GeoGebra.
