JUMP TO TOPIC
Dividend|Definition & Meaning
Definition
The dividend in mathematics is the value which is divided by another value to obtain the result. The dividend is the starting point for any division method. The dividend is one of four critical components of the division process. It is the whole that is to be divided into equal parts.
For example, if 10 divided by 2 equals 5, then 10 is the dividend, which is divided into two equal parts, while 2 is the divisor, quotient is 5, and remainder is 0.
Dividend
When we use the division method in arithmetic, we can see four related terms “ dividend, divisor, quotient, and remainder”.
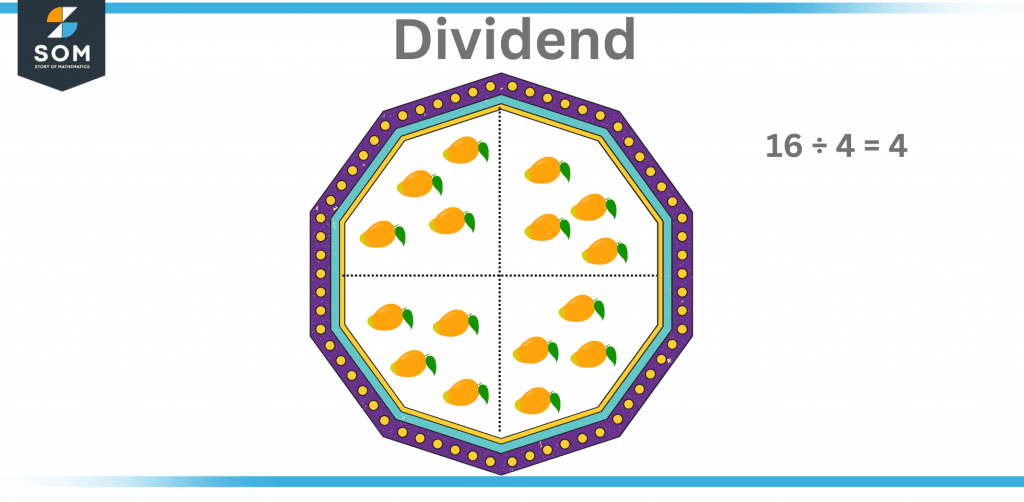
Figure 1 – Illustrating the dividend in terms of division.
There are four basic operations addition, multiplication, division, and subtraction. These fundamental operations were covered in our primary school classes. One of the fundamental arithmetic operations is division. This article will discuss the term “Dividend” in Math, with numerous solved examples.
A dividend is either a whole number or the total number of things that must be divided into equal parts. If the given number cannot be divided equally, division is the process of dividing it into equal parts and leaving a remainder. The dividend is a critical component of division operations.
The Role of the Dividend in Division?
When we divide any number m by any number n (m÷ n), the letter ‘m‘ refers to the dividend. Let us illustrate this with an example. 40 divided by 10 equals 4. For the given example, let us write the division fact.
In division 40 ÷ 10. The dividend is 40 in this case. In the division process, the dividend is the number that is completely divided by the divisor, leaving a result as the remainder. In other words, the whole must be subdivided into parts.
For example, 15 apples must be distributed among three children. The dividend in this case is 15. The division can be done in a variety of ways. Let us look at how to identify the dividend in various representations.
How To Locate a Dividend
The dividend is divided into equal groups by divisor in the division. In a problem of division, the dividend is the whole number that is being divided, and that number that divides the dividend is known as the divisor. A division fact can be represented in three ways. The results are the same across all forms. See the figure that has been shown below, which depicts the various methods of writing a dividend.
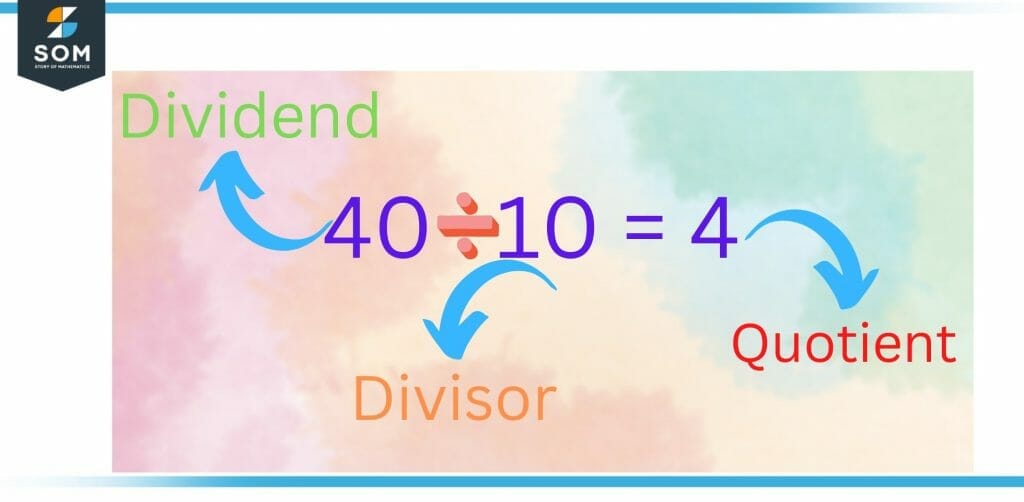
Figure 2 – First Method of Writing Dividend
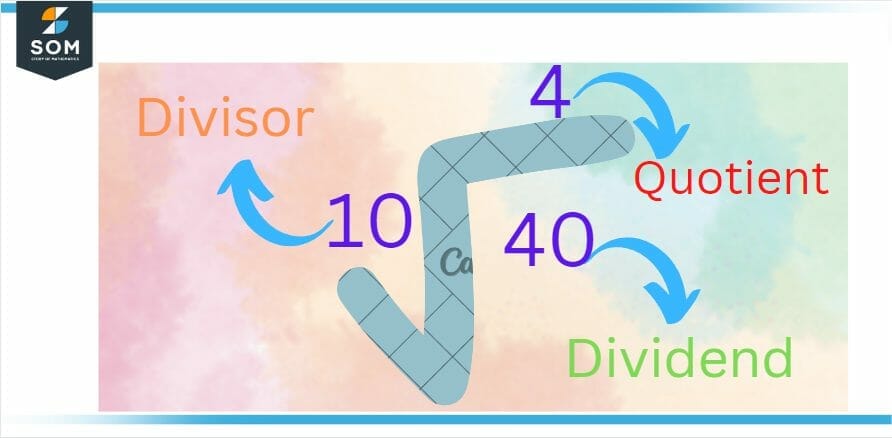
Figure 3 – Second Method of Writing Dividend
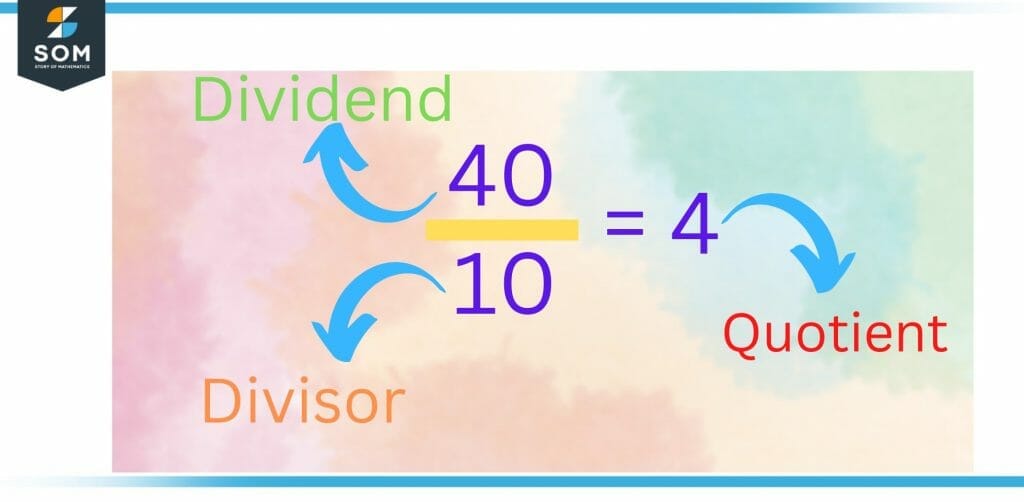
Figure 4 – Third Method of Writing Dividend
How To Locate a Dividend
Division operation is impossible without dividends. Let us suppose we need to divide 80 by 10. It can be represented mathematically as a division fact, such as 80÷ 10 = 8. This divisional fact is
- The dividend is the number 80. It is the number that must be divided. The divisor is the number 10. The dividend is divided by this number.
- The quotient is the number 8.
- The remainder in the preceding case is zero.
To thoroughly verify division, the formula for finding dividends we can used, also known as the division formula. Consider the following formula.
(Divisor x Quotient) + Remainder = Dividend
Consider another example in which we will find the dividend using the previously mentioned formula.
- dividend = x
- divisor =10
- quotient = 8
- rest = 0
When we substitute the value in the formula, we get x = (10 x 8 + 0) = 80. As a result, the dividend is worth 80. Let us look at the formula for calculating dividends when the remainder is zero. In this case, the formula will be:
• If the remainder is zero, Dividend = (Divisor x Quotient).
Fractional Dividend
Fractions are numbers that are represented as p/q. for example 1/8, 1/5, 5/4, and so on. A fraction of a whole is a group of items or a collection that has been divided into equal parts or sections. In every fraction, there is a numerator and a denominator.
- The dividend is the numerator part of a fraction.
- The divisor is the fraction’s denominator.
Difference Between the Dividend and the Divisor
The dividend and the divisor are the two most important parts of the division fact. We can’t divide the dividend without a divisor, and we can’t divide without a dividend. The dividend is divided into equal parts by the divisor, whereas the dividend is divided equally by the divisor.
Let us prove this point with an example.
For example, divide 48 by 4
Division fact = 48 ÷ 4
The dividend is 48, and the divisor is 4. We cannot divide with a single term if any of the terms are missing. Hence, 48 ÷ 4 = 12. The quotient, in this case, is 12.
Facts About Dividends
The facts about dividends in the division are as follows.
• When the dividend and divisor in a division problem are equal, the result of the division problem is always 1. For instance, 45 ÷ 45 = 1
• If the remainder is zero, the dividend has been completely divided by the divisor.
• When the dividend and quotient of a division fact are equal, the divisor has the value 1. 75 1 = 75, for example.
• When the divisor exceeds the dividend, the resultant number is a decimal number. For instance, 75 1000 = 0.075
Solved Examples
Example 1
Determine the dividend for x / 10 = 50 and verify your answer.
Solution
Assume x / 10 = 50. We understand that Dividend / Divisor = Quotient.
Dividend = Quotient x Divisor x = 10 x 50 Dividend = Quotient x Divisor x = 10 x 50 x = 500
As a result, the dividend, x, is 500.
Validation: x/10 = 50. The value of x is substituted as:
500/10 = 50
50 = 50
As a result, L.H.S = R.H.S, which has been verified.
If the divisor, quotient, and remainder value are known, the dividend can be calculated as follows:
Step 1: Add the divisor and quotient together.
Step 2: To the result of step 1, add the remainder value.
Example 2
If the quotient is 4, the divisor is 10, and the remainder is 3, find the dividend.
Solution
Given are the following values: divisor = 10, quotient = 4, and remainder = 3.
Step 1: Multiply 10 and 4. The answer is 40.
Step 2: Combine the product and the remainder. Since 40+3 = 43, the dividend is 43.
Example 3
A school decided to take its students to the science museum. There will be 100 children on the trip, and four buses will be available. Can you estimate the number of children who can fit in each bus? Determine the dividend by forming the division fact for the given problem.
Solution
To determine the number of children in each bus, divide the total number of children by the number of buses.
Here, we will divide 100 by 4.
100 ÷ 4 = 25 (here, 100 is the dividend, 4 is the divisor, and 25 is the quotient)
As a result, each bus can accommodate 25 children.
All images/mathematical drawings were created with GeoGebra.
