Double|Definition & Meaning

The concept of doubling can also be applied to other areas of mathematics, such as geometry and algebra. In geometry, for example, a line segment can be said to be double the length of another line segment if its length is twice as long. 

In algebra, the concept of doubling can be used to solve equations by isolating a variable on one side of the equation and then multiplying or dividing it by 2.

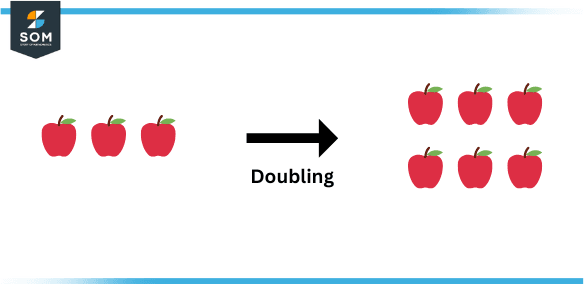
Figure 1: Example of doubling

Different Ways to Double

The concept of doubling is a fundamental concept in mathematics that is used in a variety of different contexts. And there are multiple ways for it.

Addition

You can use the “+” operator to double a number, for example:

number + number = double

For example: 5 + 5 = 10

Another way to double a number is to add it to itself. For example, if you want to double the number 5, you would perform the calculation 5 + 5 = 10. The result, 10, is the double of the original number 5.

Multiplication

In multiplication, you simply need to multiply it by 2. For example, if you want to double the number 5, you would perform the calculation 5 * 2 = 10. The result, 10, is the double of the original number 5.

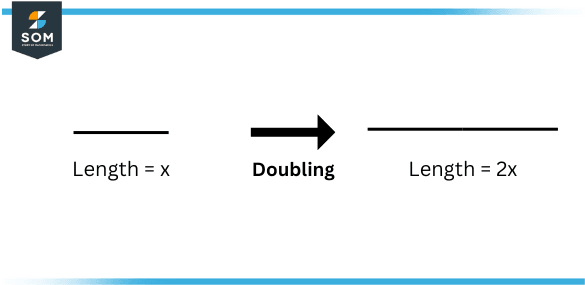
Figure 2: Doubling length of a line

Subtraction

In subtraction, the concept of “doubles” is often used as a strategy to make the problem easier to solve. The strategy of using doubles in subtraction involves breaking down a subtraction problem into two parts, each of which is half of the original problem.

For example, let’s say you want to subtract the number 15 from the number 20. Instead of subtracting 15 from 20 directly, you can use the strategy of doubles by breaking the problem down into two parts:

• Subtracting 10 from 20
• Subtracting 5 from 10

The first step is to subtract 10 from 20, which gives you the result of 10. The second step is to subtract 5 from 10, which gives you the final result of 5.

By breaking down the subtraction problem into two parts, each of which is half of the original problem, you can use the concept of doubles to make the problem easier to solve. This strategy can also be applied to subtraction problems involving larger numbers. For example, if you wanted to subtract 38 from 50, you could break the problem down into two parts:

• Subtracting 25 from 50
• Subtracting 13 from 25

The first step is to subtract 25 from 50, which gives you the result of 25. The second step is to subtract 13 from 25, which gives you the final result of 12.

This method is particularly useful for young students and people who are learning subtraction. It can help them to understand the subtraction concept and make it more manageable.

Double in Computer Science

In computer science, the term “double” is used to describe a data type that can store a number with twice the precision of a single-precision data type. This data type is often used to represent decimal numbers and is commonly used in scientific and engineering calculations.

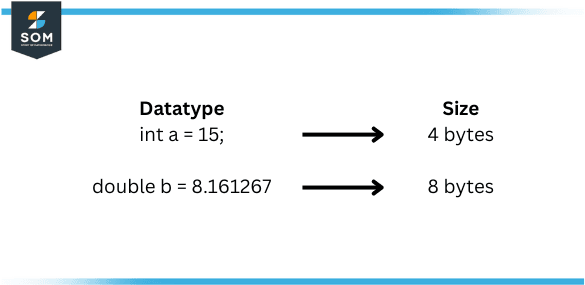
Figure 3: Double datatype in Computers

A double-precision floating-point number is a type of number that uses 64 bits of memory to store its value. This allows for a much larger range of numbers to be represented compared to a single-precision floating-point number, which only uses 32 bits. The double-precision also provides greater precision, meaning that it can represent decimal numbers with more digits after the decimal point.

For example, a single-precision floating-point number can represent the value 3.14159265 up to 7 decimal places, while a double-precision floating-point number can represent the value up to 15 decimal places 3.141592653589793.

Because of the increased precision and larger range of numbers that can be represented, double-precision floating-point numbers are often used in scientific and engineering calculations where a high level of precision is required. For example, in simulations, weather forecasting, and other high-precision numerical computations.

It’s important to note that while double-precision floating-point numbers provide greater precision than single-precision floating-point numbers, they are still not capable of representing certain numbers exactly, such as some irrational numbers. Therefore, it’s important to be aware of the limitations of this data type when using it in computations.

Overall, the double data type is an essential tool in computer science, and it’s used in many applications that require high precision and large range of numbers representation. It is a fundamental concept that is used in a variety of different areas, such as scientific and engineering calculations, simulations, and other high-precision numerical computations.

It’s also possible to use a programming language to double a number by using the appropriate operator or function. For example, in Python, you could use the “*” operator to double a number:

x = 5 # integer 5

x = x * 2 # multiplies by 2 (double)

print(x)  # Output: 10

The above code takes the number 5, multiplies it by 2 (doubles it), and then prints (shows to the user) the output, which would be 10.

In C++, you could use the “*” operator as well:

int x = 5; // integer 5

x = x * 2; // multiply by 2 (double)

cout << x;  // Output: 10

The above code does the same thing as the previous one, just in a different programming language.

In most programming languages, there is usually a function or operator that can be used to double a number; it’s just a matter of finding the correct one for your specific language or context.

Example Question

Q: If the length of a rectangle is double the width, and the perimeter is 40, what is the length of the rectangle?

Solution

Let’s call the width of the rectangle “w” and the length of the rectangle “l.”

From the problem statement, we know that the length of the rectangle is double the width, so we can write the equation: l = 2w

We also know that the perimeter is 40, and the perimeter of a rectangle is given by the formula: P = 2l + 2w

Substituting the first equation into the second equation, we get: 40 = 2(2w) + 2w 40 = 6w

Now we can solve for the width by dividing both sides by 6: w = 40/6 w = 6.67

Finally, we can use the equation l = 2w to find the length of the rectangle: l = 2(6.67) l = 13.33

Therefore, the length of the rectangle is 13.33 units.

All mathematical drawings and images were created with GeoGebra.

Dot Plot Definition < Glossary Index > Dozen Definition