JUMP TO TOPIC
Duodecimal|Definition & Meaning
Definition
The word “Duodecimal” comprises two words, duo and decimal. “Duo” means “two” and “decimal” means “ten”. Two and ten add up to twelve. A duodecimal number system is a base-12 number system also known as the dozenal number system.
Figure 1 shows the twelve basic numerals of a duodecimal number system.
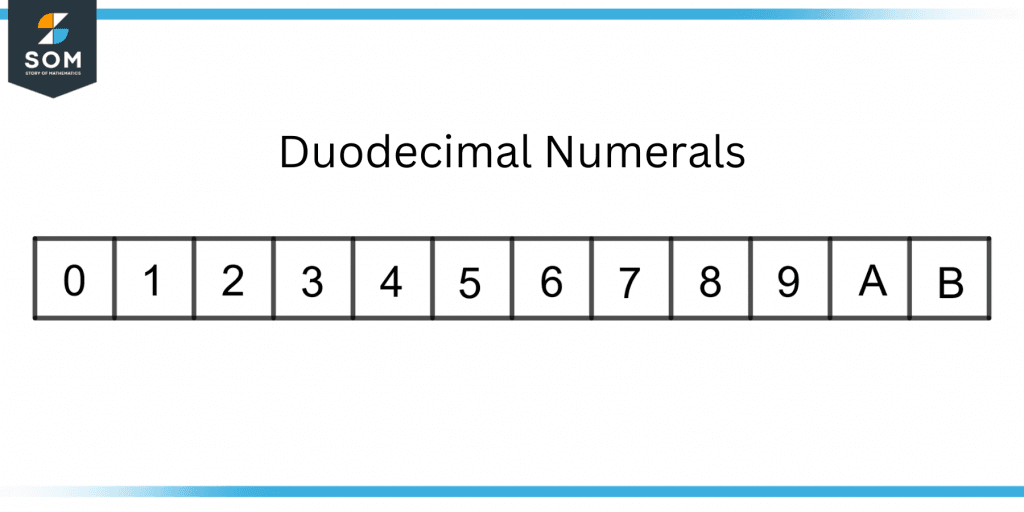
Figure 1 – A Duodecimal Number System
Comparison of Decimal and Duodecimal Systems
A decimal number system is a base-10 system having unique numbers that are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
From 0 to 9, the duodecimal system is similar to a decimal system. For the numbers 10 and 11, the characters A and B are used.
These numerals from 0 to 9, A, and B make the twelve unique notations of a duodecimal system. Figure 2 shows the decimal and duodecimal numbers side by side.
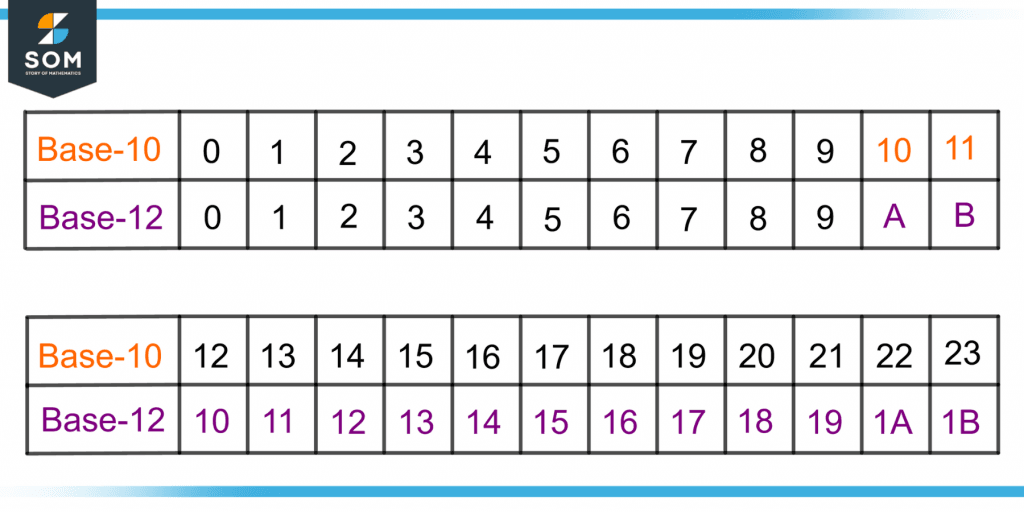
Figure 2 – Comparison of Decimal and Duodecimal Systems
The following terms are important in the duodecimal system.
Dozen
A “dozen” is twelve units. It is similar to “tens” in the decimal system. So, the number “12” in the decimal system is the number “10” in the duodecimal system.
Also, “10” would be “one dozen and zero units” and “12” would be “one dozen and two units” in the duodecimal system. But a “one dozen and two units” is 14 in the decimal system.
Also, “0.1” in decimal is one-tenth but in duodecimal it is one-twelfth.
Gross and Great Gross
A hundred in duodecimal is called a gross and a thousand is called a great gross.
Duodecimal System – An Optimal System
The base 12 of the duodecimal system has the factors (1, 12), (2, 6), and (3, 4). It has more factors than the decimal system that are (1, 10) and (2, 5).
For the octal system, the factors of 8 are (1, 8) and (2, 4). Similarly, the base-6 system has the factors (1, 6) and (2, 3).
The highest number of factors of 12 makes the duodecimal system an optimal system. It is considered superior to the decimal system.
It has fewer numerals as compared to a hexadecimal system and more factors than any of the systems with a base of less than 12.
Historical Importance of the Duodecimal System
In ancient times, many civilizations used the duodecimal system for the units of time. Historically, it was established that a year has 12 months and there are 12 hours in a day but it was later on changed to 24.
Figure 3 shows a clock with 12 duodecimal numbers.
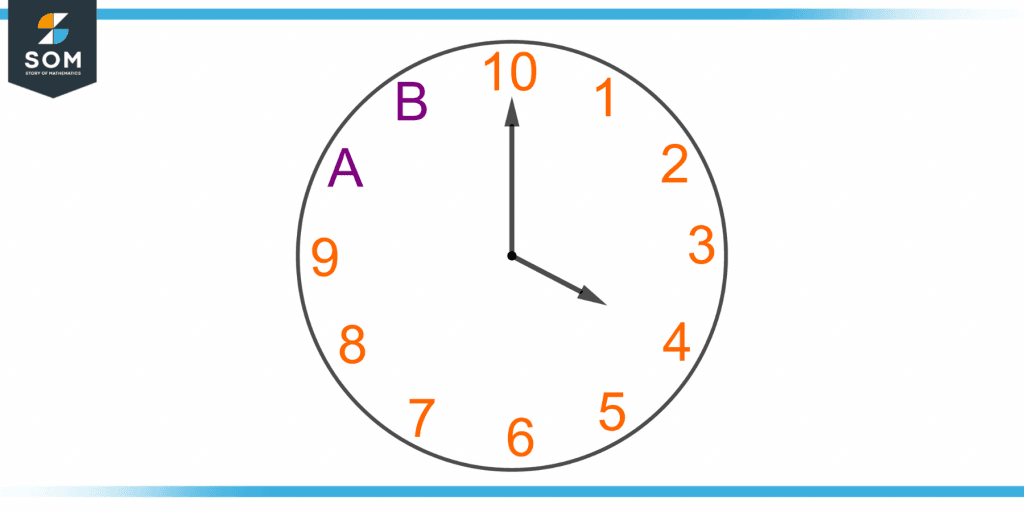
Figure 3 – A Clock With Duodecimal Numerals
The clock shows another set of duodecimal numerals. Notice that 10 and 11 are always written with different symbols i.e. A and B in the duodecimal system.
The number 12 has an essential role in measurements. For example, a foot is equal to 12 inches and a pound is made of 12 ounces. In Old Britain currency, a shilling had 12 pennies in it.
The 12 phalanges on the four fingers of a hand excluding the thumb and the 12 lunar cycles per year specify the importance of the duodecimal system.
Notations for Ten and Eleven
Different notations can be used for the duodecimal ten and eleven. Upside-down 2 and 3 are also used but make typewriting difficult.
Figure 4 shows a different notations used for the numbers 10 and 11.
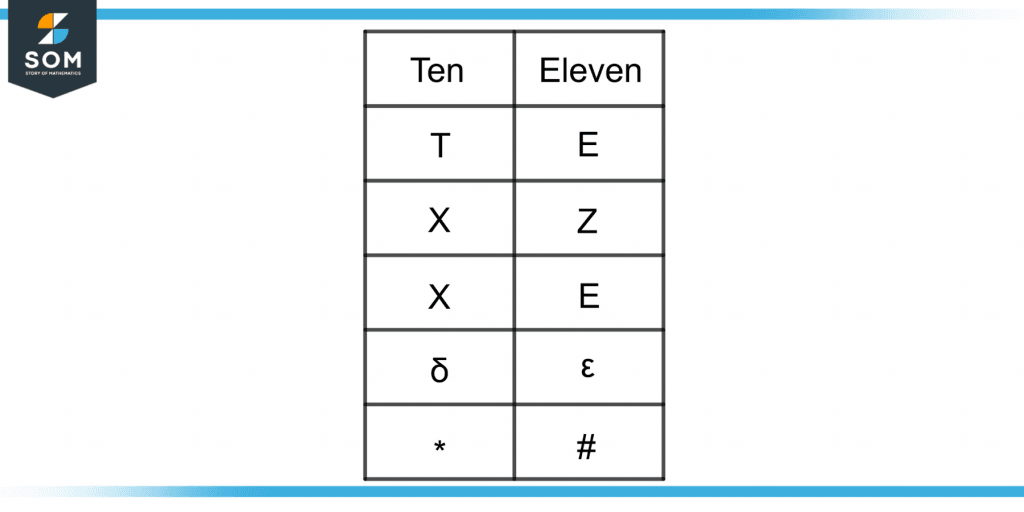
Figure 4 – Different Notations for Ten and Eleven in Duodecimal System
Different Base Notations
There are different ways to represent a duodecimal number. The base-12 number can be written in italics to distinguish it from a decimal number.
For example, the duodecimal 28 is equal to decimal 32 and can be expressed as:
28 = 32
It can also be written with a subscript of the base number as:
${(28)}_8$ = ${(32)}_{10}$
Similarly, the subscripts z and d can be used instead of 8 and 10 respectively.
Also, the notations “dec” and “doz” are used for decimal and dozenal systems respectively as:
doz 28 = dec 32
A semicolon is used for the decimal point in a dozenal number such as:
${(20;6)}_8$ = ${(24.5)}_{10}$
Names of Duodecimal Numbers
The word “qua” is used at the end for the whole numbers that have a positive power of 12. Whereas, the “cia” ending is used for the fractions having a negative power of 12.
Also, the prefixes un, bi, tri, quad, pent, hex, sept, and oct specify the number of zeros after the digit one.
Base Conversions
For the base conversions given below, the alphabets T and E are used for ten and eleven in the duodecimal system.
Decimal to Duodecimal
The base-10 number can be converted to a base-12 number by dividing it by 12 until its quotient becomes zero.
For example, the decimal number 2146 is divided by 12 to get a quotient of 178 and a remainder of 10. 10 is T in duodecimal.
The number 178 is again divided by 12 to get 14 as a quotient and a remainder of 10 which is T. 14 divided by 12 gives 1 as the quotient with remainder 2.
The duodecimal number starts from the last quotient that is less than 12 to the remainder going in the upward direction. Figure 5 shows the repeated divisions of 2146 by 12.
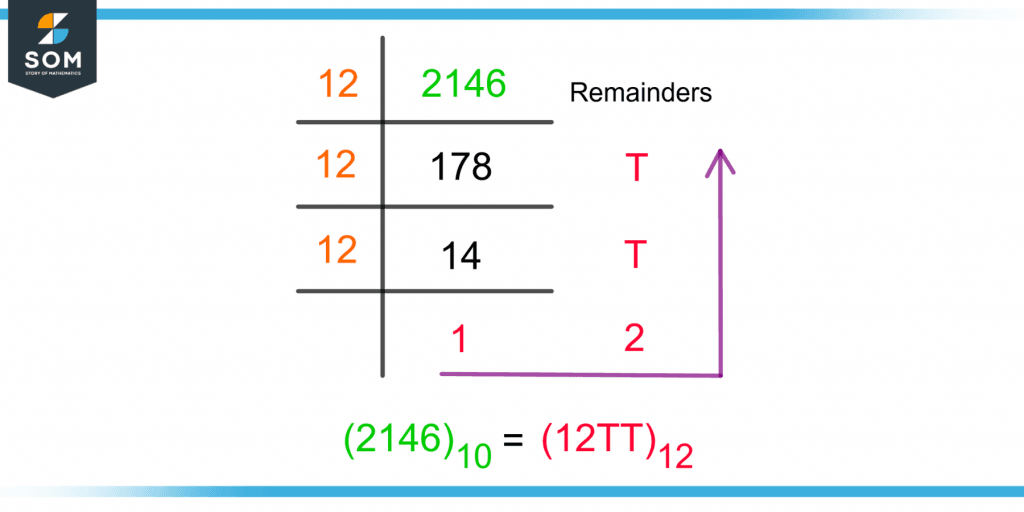
Figure 5 – Converting a Decimal Number Into a Duodecimal-Number
So, base-10 number 2146 in base-12 is:
$(2146)_{10}$ = $(12TT)_{12}$
Duodecimal to Decimal
A duodecimal number can be converted to a decimal number by the place values of a base-12 number.
The right-most numeral of the base-12 number holds the 12 to the zero power and this power increases by 1 as we move towards the left.
For example, $(T34)_{12}$ needs to be converted to base-10. Figure 6 shows the place values of the power of 12 in $(T34)_{12}$ and its decimal conversion.
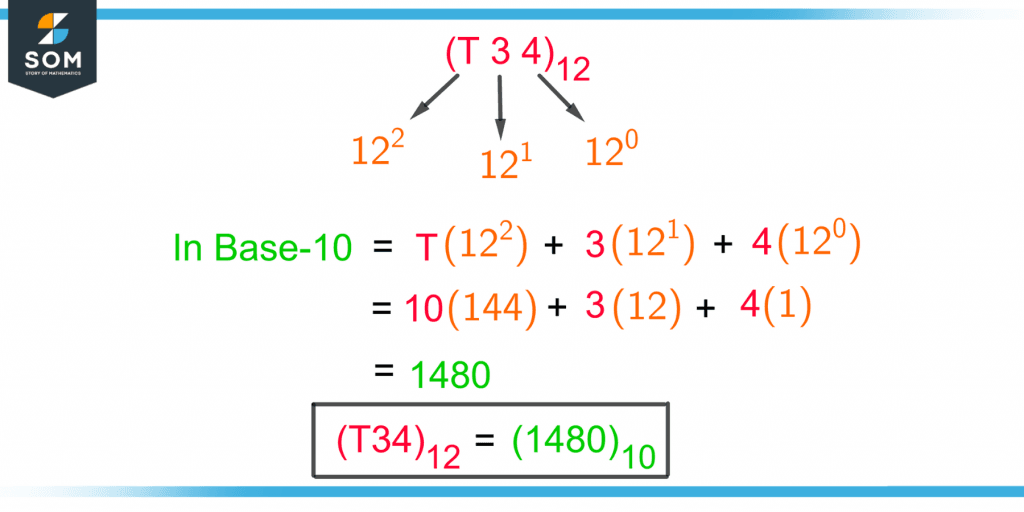
Figure 6 – Converting a Duodecimal Number Into a Decimal Number
An Example of COnversion from Duodecimal to Decimal
Convert the duodecimal number 8612 into a decimal number.
Solution
The weights of 12 increasing from 0 from right to left are multiplied by each digit and added to give the desired decimal number as follows:
8612 in Base-10 = [ 8 ${(12)}^3$ ] + [ 6 ${(12)}^2$ ] + [ 1 ${(12)}^1$ ] + [ 2 ${(12)}^0$ ]
8612 in Base-10 = [ 8(1728) ] + [ 6(144) ] + [ 1(12) ] + [ 2(1) ]
8612 in Base-10 = 13,824 + 864 + 12 + 2
8612 in Base-10 = 14,702
So:
$(8612)_{12}$ = $(14,702)_{10}$
All the images are created using GeoGebra.
