e Euler’s Number|Definition & Meaning

This irrational number is a part of logarithms as ‘e’ is considered the natural base of the logarithm. These concepts are not only used in maths but are also used in other subjects like physics.  

Introduction to Euler’s Number

Euler’s number has great significance in the field of mathematics. This term has been named after the great swiss mathematician Leonard Euler. The number ‘e’ along with π, 1, and 0 are used in the formation of the Euler Identity. 

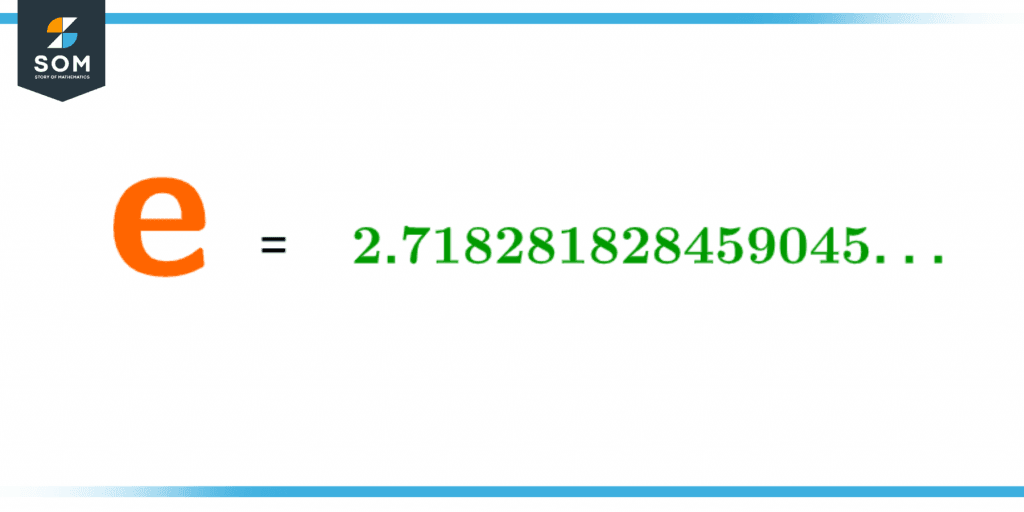
Figure 1 – Infinite value of e.

Euler’s number is mostly used in exponential distribution:

exponential distribution = $\displaystyle \lambda e^{-\lambda t}$

We use it to solve problems related to increases or decreases of a non-linear function. Mostly we calculate the growth or decay of the population. For $\lambda$ = 1, the maximum value of the function is 1 (at x = 0), and the minimum is 0 (as x $\to \infty$, $e^{-x} \to 0$).

 Euler’s number forms the base for the natural logarithm, so the natural logarithm of e equals 1.

log_e = ln

ln e = 1

The Euler number is also given by the limit {1 + (1/n)}n, where n gradually approaches infinity. We can write it as:

\[ e = \lim_{n\to\infty} f\left(1 + \frac{1}{n}\right) \]

So by adding the value of ‘e,’ we can get our desired irrational number.

Complete Value of Euler’s Number

Euler’s number, which is represented by the ‘e,’ is equal to approximately 2.718. But actually, it has a large set of numbers to represent it. The complete value can go up to 1000 digits. The credit for finding and calculating such a huge figure goes to Sebastian Wedeniwski. Today we know the values to go about 869,894,101 decimal places. Some of the initial digits are as below:

e = 2.718281828459045235360287471352662497757247093699959574966967627724076…

Methods To Calculate Euler’s Number

We can calculate the Eulers number by using these two methods which are:

1. \[ \lim_{n\to\infty} f\left(1 + \frac{1}{n} \right) \]
2. \[ \sum_{n=0}^{\infty} \frac{1}{n!} \]

We put values in these formulas to get our results. Let us see these methods in detail:

First Method

In this method, we look into the end behavior to get the values of ‘e.’ When we form a graph using the above-given formula, we get horizontal asymptotes. As the lines go away from 0, we get a function with finite limits. This tells us that if we increase the value of x, ‘e’ will be closer to the y-value.

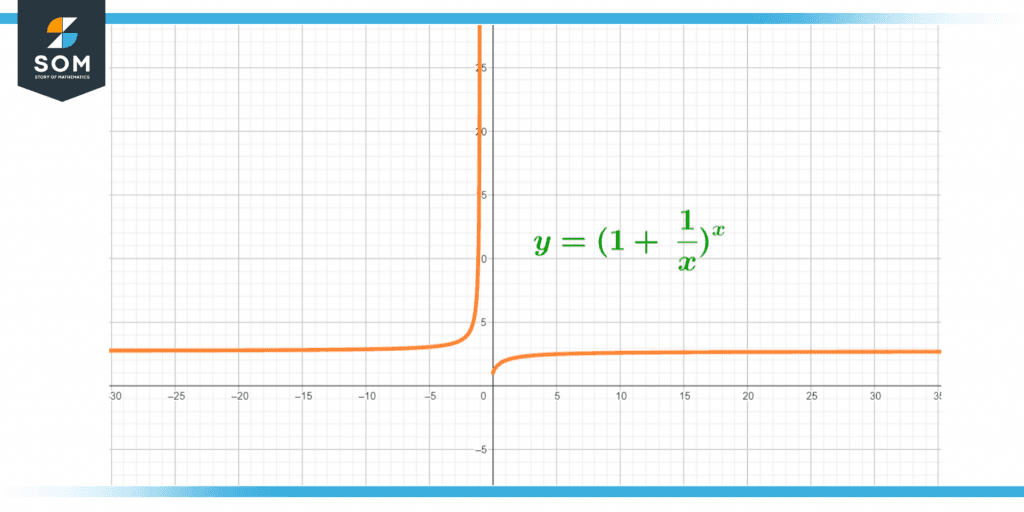
Figure 2 – Horizontal asymptotes due to an increase in the value of x.

Second Method

We use the concept of factorial in this method. To calculate a factorial, we multiply the given number by every positive integer that is less than that number and greater than zero. We represent factorial with ‘!’ (exclamation mark).

\[ e = \sum_{n=0}^{\infty} \frac{1}{n!} \]

\[ \sum_{n=0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{1 \times 2} + \frac{1}{1 \times 2 \times 3} …\]

Or:

\[ \sum_{n=0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} \dots \]

So, we get the following:

\[ e = \frac{1}{1} + \frac{1}{1} + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} + \dots \]

Summing the first six terms:

\[e = \frac{1}{1} + \frac{1}{1} + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} = 2.71828\]

Properties of Euler’s Number

Below, we list some properties of Euler’s number:

• It is an irrational number that keeps on going until infinity.
• Euler number is used to explain the graphs and conditions of exponential growth and decay of radioactivity.

Figure 3 – Exponential Growth in Radioactivity

• Euler’s number is the base of the all-natural logarithm.
• Euler’s number is transcendental, just like pi.
• Euler’s number is such a constant whose limit approaches infinity.
• We calculate it in terms of infinite series by adding all the terms.
• There is a difference between Euler’s number and Euler’s constant. Euler’s constant is also an irrational number which also never ends.

Euler’s Constant = 0.5772156649 

• Euler’s number is used in almost every branch of mathematics.

Solved Examples of Euler’s Number

Example 1

Selena has to give $280 to Blair with an interest rate of 2% that is compounded continuously. How much will Blair have by the end of the 4 years?

Solution

We will use this formula:

A = Pe$\displaystyle\mathsf{^{Rt}}$

Let us put the values in this formula:

A = 280e$\displaystyle\mathsf{^{0.02 \times 4}}$

A = 280 x 1.0832

A = 303.296

Hence the money that Blair will have by the end of 4 years will be $303.296.

Example 2

Two friends decided to invest money in saving accounts that offer interest rates according to the money that has been deposited. Help them find out how much will they have at the time of withdrawal. 

1. Atlas invested $7000 in an account which offered 3.5% interest every year that compounded continuously. How much will he get after 4 years?
2. Ryle invested $1200 in an account which offered 2% annual continuously compounding interest. What will be his returns after 10 years?

Solution

1. For Atlas’s case we will use the following formula:

FV = PVe$\displaystyle\mathsf{^{Rt}}$

Now putting the following values: PV = 7000, R = 0.035, and t = 4 we get,

FV = 7000e$\displaystyle\mathsf{^{0.035 \times 4}}$

FV = 7000e$\displaystyle\mathsf{^{0.14}}$

FV = 7000 x 1.150

FV = 8051.7

So Atlas will have $8051.7 after 4 years.

2. For Ryle’s case, we will use the following formula:

FV = PVe$\displaystyle\mathsf{^{Rt}}$

Now putting the values PV = 1200, R = 0.02, and t = 10, we get:

 FV = 1200e$\displaystyle\mathsf{^{0.02 \times 10}}$

FV = 1200e$\displaystyle\mathsf{^{0.2}}$

FV = 1200 x 1.221

FV = 1465.6

So Ryle will have $1465.6 after 10 years.

Example 3

State some applications of Euler number in the field of mathematics.

Solution

Euler’s number holds a significant place in both mathematics and physics. Some of its applications are:

1. Radioactivity decay and growth
2. Compound interest
3. Probabilistic modeling (exponential, Gaussian/normal)
4. De-arrangements
5. Optimal planning problems
6. Asymptomatics

These are some of the many applications of  Euler’s number $e$.

Images/mathematical drawings are created with GeoGebra.

Duodecimal Definition < Glossary Index > Element Definition