JUMP TO TOPIC
Element|Definition & Meaning
Definition
The things that go into making up a set are referred to as its elements or its members. Commas are used to denote individual components of a set, which are often written between a set of curly braces but also enclosed in parentheses. When referring to a set, the name of the collection should always be written with capital letters.
Sets and elements are two notions that are essential to the study of mathematics. An individual item or a single component of something is referred to as an element, whereas a set is a group of components that belong together.
Mathematical objects are defined, organized, and classified with the help of elements and sets, which together comprise the fundamental building blocks of the discipline.
The following illustration provides a graphical representation of one of the elements that make up a set. The elements are 1,2,3,4 and 5.

Figure 1 – Representation of element
What Is an Element?
It doesn’t matter what it is; a number, a word, a structure, or even an idea could be considered an element. It is a standalone component that is integrated into the building of other things or the conception of new concepts.
To give one illustration, the digits 1, 2, 3, and 4 are all components of the collection of natural numbers. The characters A, B, C, and D are all examples of letters that are included in the collection of letters that make up the English alphabet.
The black, white, and gray colors are all examples of elements that can be utilized to symbolize thoughts. In mathematics, elements can also stand in for symbols like the plus sign (+), the minus sign (-), and the equals sign (=).
What Is Set?
A collection of items that have been arranged in a certain fashion is referred to as a set. Sets are typically indicated by the notation ” ” and include traces that have been gathered together according to a certain criterion. For instance, the set of natural numbers is represented as “1, 2, 3, 4, 5,…”, and the set of letters in the English alphabet is represented as “A, B, C, D, E,…”. Both of these sets are written in the same way.
Mathematical Sets
In math, sets are frequently used to describe the individuals that make up a given group, such as the collection of students that are enrolled in a particular class. The relationships between the elements can also be represented using sets in some contexts. For instance, the collection of all even integers is represented by the notation “2, 4, 6, 8, 10,…”. Due to the fact that each component in this set is an even number, the elements in this set are connected to each other in some fashion.
In a similar vein, the set of all squares could be represented by the notation “1, 4, 9, 16, 25,…”. This collection includes elements that are connected to each other in the sense that each element is a square that is unimpaired in any way.
Mathematics employs a wide variety of concepts, including elements, sets, relations, and operations, in addition to the more familiar elements and sets. Relationships are employed to describe the connection between two groups of elements, whereas functions are employed to depict the connection between two groups of elements.
Calculations and manipulations of elements are accomplished through the use of operations. For instance, adding is an operation that may be utilized in the process of combining two or more constituent parts. In a nutshell, two notions that are essential to the study of mathematics are sets and elements.
Individual things or units are referred to as elements. Sets, on the other hand, are groups of components that have been arranged in a specific fashion. Mathematical objects are defined, organized, and classified with the help of elements and sets, which together comprise the fundamental building blocks of the discipline.
What Constitutes the Individual Parts of a Set?
Take the following as an illustration:
A = {1, 2, 3, 4, 5 }
owing to the fact that a group is frequently denoted by a capital letter.
Therefore, the set is denoted by the letter A, while the numbers 1, 2, 3, 4, and 5 correspond to the elements or members of the set.
It is not possible to repeat any of the components that are listed in the set, but they can appear in any order. Each and every component of the set is denoted by a lowercase letter in the case of the alphabet. Additionally, we have the option of writing it as 1 over A, 2 over A, etc. The number 5 is the highest cardinal value in this collection. The following are some sets that are frequently used:
- N: The complete set of natural numbers
- Z: The complete set of integers
- What is the whole set of rational numbers?
- R: The complete set of real numbers
- Set of all positive integers, denoted by Z+.
Order of Sets
The number of components in a set can be determined by looking at its order. It provides information regarding the extent of a set. The cardinality of a set is another name for the order of the set. The size of the set, whether it is a finite set or even an infinite set, is referred to as the set’s “order,” which can either be finite or infinite, depending on the size.
What Exactly Is the Distinction Between Sets and Elements?
In mathematics, the terms “element” and “set” are two distinct notions that are used to represent distinct groups of things that are gathered together. An individual component of a set is referred to as an element, whereas the collective members of a set are referred to as a set. An individual component of a set is called an element.
For instance, the set “1,2,3” comprises the numbers 1, 2, and 3. Each of these components is capable of functioning independently and can be modified in its own right. A connection among two or more sets can also be characterized by using elements in this way. For instance, if two different sets, A and B, both contain the element ‘x,’ then ‘x’ is an element of both of the aforementioned sets.
On the other hand, a collection of elements is referred to as a set. It is a collection of things that have been gathered together in one place. Each of the components that make up a set must be connected to one another in some fashion.
In most cases, the components that make up a set share some characteristic or topic in common with the rest of the collection. A set of numbers would be something like “1,2,3,” for instance. The set has no non-numerical elements; instead, all of the elements are numbered.
In conclusion, an element is a singular representative of a set, whereas a set is a collection of such representatives. A connection between two or more things can be described using elements.
Visual Representation of an Element
The graphic depicts the intersection of two sets, and the results of that intersection are the elements 1, 2, and 3.
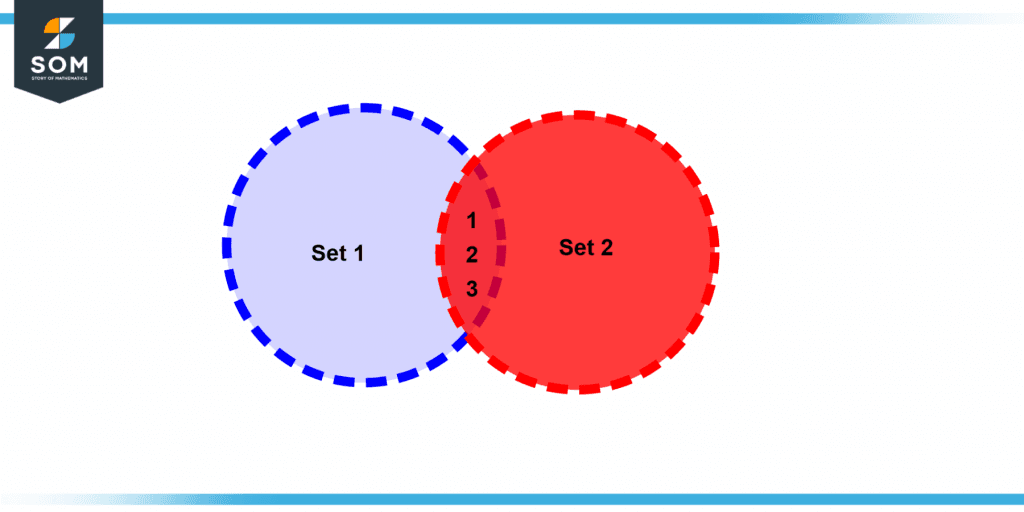
Figure 2 – Element representation in A intersection B
The below Venn diagram represents the union of two sets and its elements.
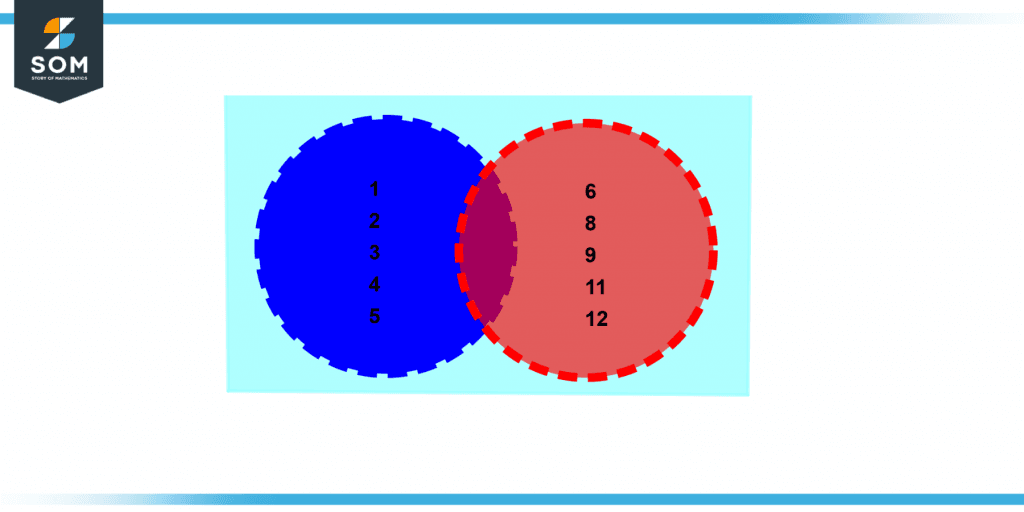
Figure 3 – Venn diagram of A union B
A Numerical Example of an Element
Example
The two sets which are A={1,2,3,4} and B={3,,45,6}. What is the intersection of these two sets and what are the elements of the intersection set?
Solution
Given that:
A={1,2,3,4}
B={3,4,5,6}
The intersection of two sets is:
= {3,4}
The elements after the intersection are:
= {3,4}
All mathematical drawings and images were created with GeoGebra.
