Elimination|Definition & Meaning

Conceptual Overview 

Figure 1 – Conceptual overview of Elimination Process

There are many ways of solving linear equations algebraically, but the elimination method is the most widely used. In the elimination method, one variable is eliminated using basic arithmetic operations, and the equation is simplified to compute the value of the second variable. To find the value of the variable eliminated, we can use any equation with the value of the variable eliminated.

Suppose there is a set of equations involving two variables x and y.In order to find the value of x and y we have to perform elimination to get the desired values. Similarly, if we want to define our equation in only one variable that also can be done by elimination. So in short elimination convert an equation involving many variables to only a few or one variable.

We perform various operations on a given set of equations for performing elimination like first multiplying the equation with some constant and then applying addition and subtraction operations on the equation. We can also take the elimination process as an aid to convert equations to a compact form.

Steps Involved in Elimination Process

Here we will discuss step by step guide to the elimination process.

Step 1

First of all according to the given data mark the set of equations as 1 or 2 or 3 depending upon the given situation.

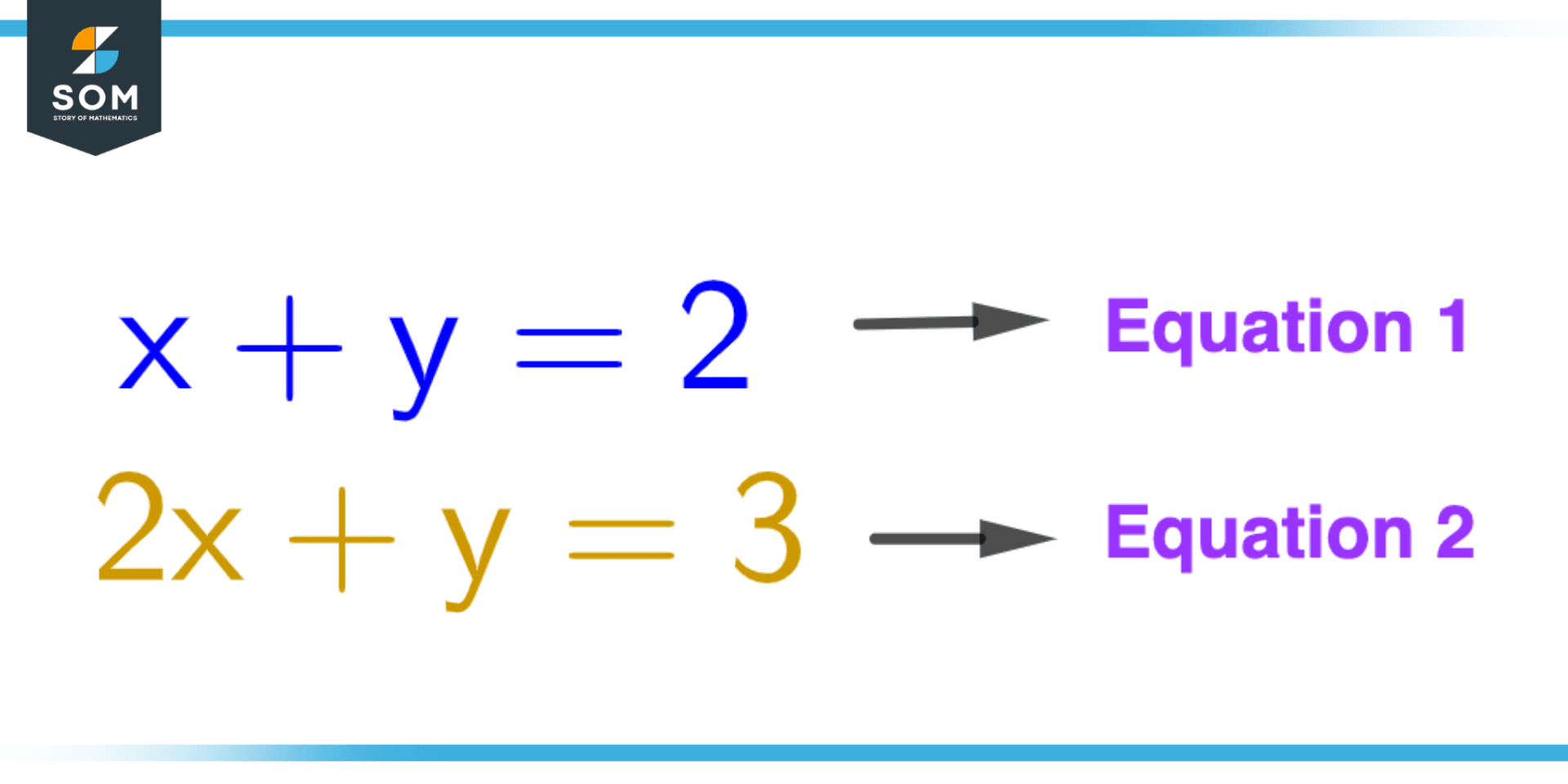
Figure 2 – Marking Numbers to equations

Step 2

After numbering multiply or divide either of the one equation with such type of a constant that will result in making the equation’s first term equivalent to the first term of the second equation, which will eventually help in getting one variable eliminated.

Normally, we should make that term equal whose variable is to be eliminated so if we want to eliminate the x term we will make the x term of both equations equal and if we want to eliminate the y term of the equation we will make the y term equal.

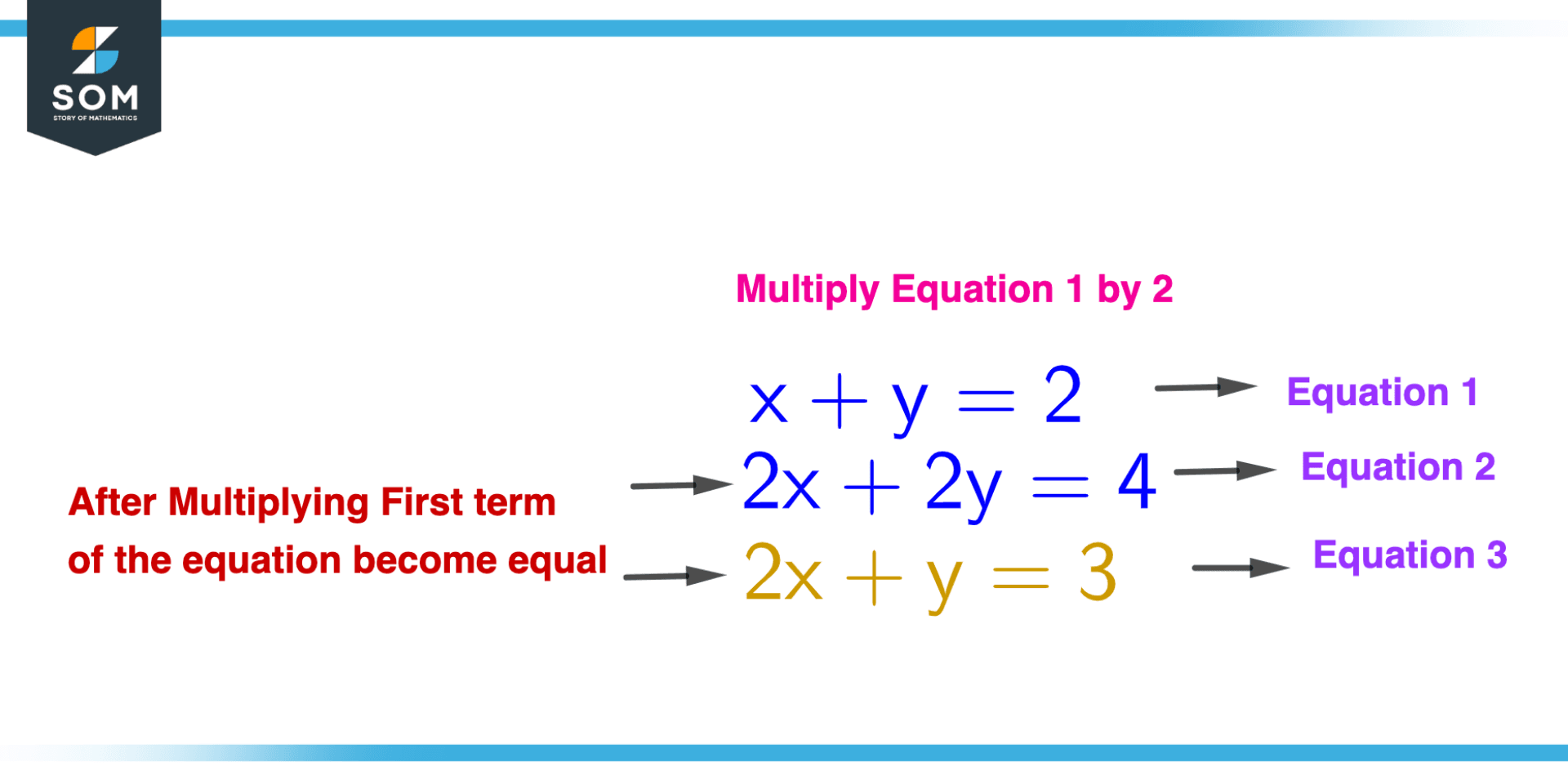
Figure 3 – Multiplying equation with constant

Step 3

When we are able to make the first term of both equations equal by multiplying or dividing, the next step is to perform arithmetic operations either addition or subtraction. The factor that will decide which operation to apply to the equation depends upon the fact that one variable must be eliminated after performing that operation. It is totally a senior dependent.

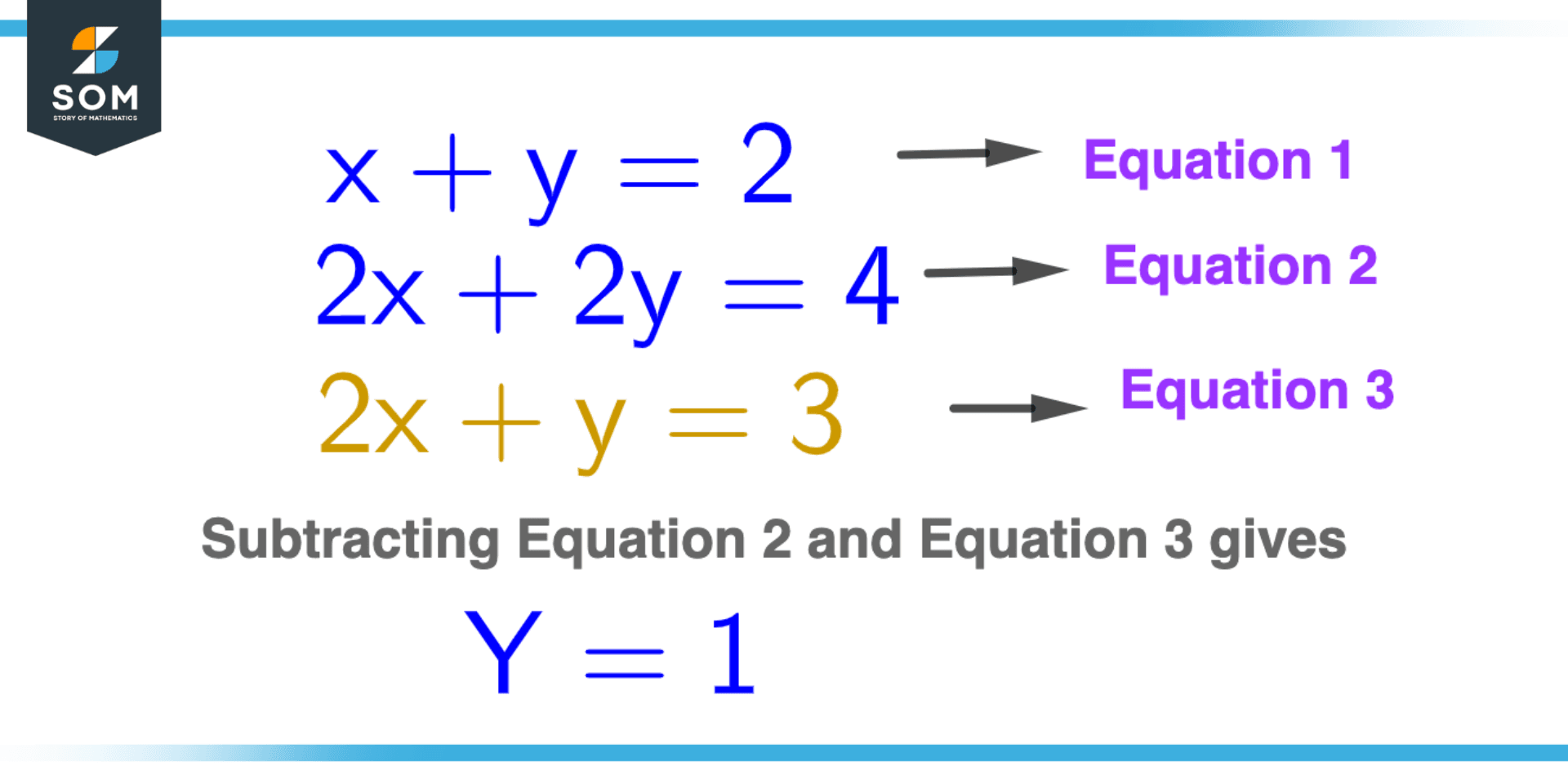
Figure 4 – Applying Arithmetic Operation on Equation

Step 4

After eliminating one variable, instead of repeating the whole process again, we can find the value of another unknown variable by just substituting the value of the first variable we get in the equation. The intuition of substitution here is to just get the answer quickly while repeating the process for another variable would be time taking.

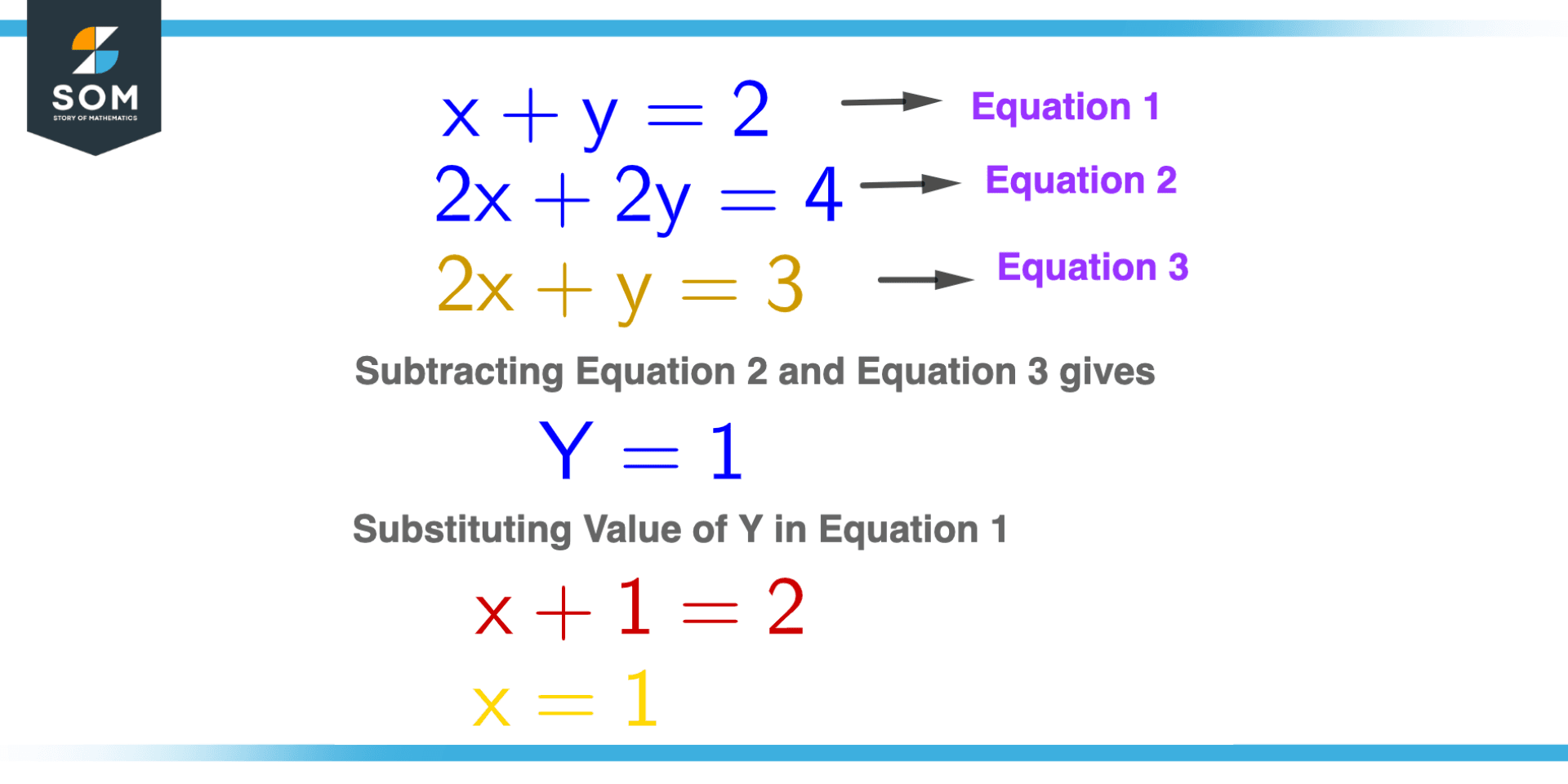
Figure 5 – Substituting Value of Variable Y in Equation

General Tips for Elimination

• If there are two equations and we want to eliminate one of the variables, we will add the equation’s first coefficients if both equations are different.For instance, x+y=2, and 3x+y=1
• If the coefficient of both equations is equal, we will subtract the equations. For instance, 2x+y=2, and 2x+3y=1
• In case one of the variables needs to be eliminated, the elimination method is preferable over substitution. In order to solve the linear equation in one variable, the previous step is to form the equation in one variable.

Elimination of Equation of Two Parallel Lines

We know that parallel lines are types of lines that never intersect each other. So in order to show the weakness of the elimination method, we will solve the equation of a parallel line to show the results. In general, there is no solution for two parallel lines. Let’s take two parallel lines:

x+y=8  (Eq. 1)

2x+2y=8  (Eq. 2)

So in order to make the first term of both equation equal, we will multiply equation one with 2 on each side, which will give:

2x+2y=16  (Eq. 3)

In order to eliminate we will subtract equation 2 and equation 3:

2x+2y-2x-2y=16-8

0=8

This is wrong as zero can not be equal to 8, which shows that we can not eliminate any variable of equations that are parallel.

Elimination of Equation of Two Coincident Lines

Coincident lines are those lines that lie exactly on top of one another or in other words one of the lines is just multiplied by some scale factor. Here we will show that elimination is not applicable to any variable of coincident lines. Suppose two coincident lines below:

x+y=4  [Eq. 1]

2x+2y=8  [Eq. 2]

We can see equation 2 is scaled two times that of equation 1 making it coincident.

To make the first term of equation 1 equal to the first term of equation 2, we will multiply equation 1 with 2, which will result in the following:

2x+2y=8  [Eq. 3]

So in order to eliminate either the x or y variable, we will subtract equation 2 and equation 3, which will give us the following:

2x+2y-2x-2y=8-8

0=0

Which will give infinite solutions. So in order to avoid hassle, we always first check the type of equation then we will perform the elimination because we see the two cases where elimination is not permissible.

Solved Examples of Systems of Equations Using Elimination

Example 1

Consider the two sets of equations first eliminate the variable x and then eliminate the variable y. Equation is given as:

3x+5y=7 and 2x+3y=5

Solution

3x+5y=7  [Eq. 1]

2x+3y=5  [Eq. 2]

Eliminating Y

Multiplying equation 1 by constant 2 and equation 2 by constant 3:

2(3x+5y)=2(7) 

6x+10y=14  [Eq. 3]

3(2x+3y)=3(5) 

6x+9y=15  [Eq. 4]

Now both the equations have the coefficient of the first term equal, so will subtract both equations that will give us:

6x+10y-6x-9y=14-15

10y-9y=-1

y=-1

y=-1

Eliminating X:

3x+5y=7  [Eq. 1]

2x+3y=5  [Eq. 2]

In order to eliminate y we will make the coefficient of y term of both the equation equal, so for that purpose, we will multiply equation 1 with 3 and equation 2 with 5:

3(3x+5y)=3(7) 

9x+15y=21  [Eq. 3]

5(2x+3y)= 5(5)

10x+15y=25  [Eq. 4]

Subtracting equations 3 and 4 gives:

9x+15y-10x-15y=21-25

9x-10x=-4

-x=-4

x=4

All mathematical drawings and images were created with GeoGebra.

Element Definition < Glossary Index > Ellipse Definition