Ellipse|Definition & Meaning

Ellipse is a conic section component with properties similar to a circle. In contrast to a circle, an ellipse has an oval shape. An ellipse has an eccentricity below one and represents the locus of points whose distances from the ellipse’s two foci are a constant value. Ellipses can be found in our daily lives in a variety of places, including the two-dimensional shape of an egg and the running tracks in sporting venues. 

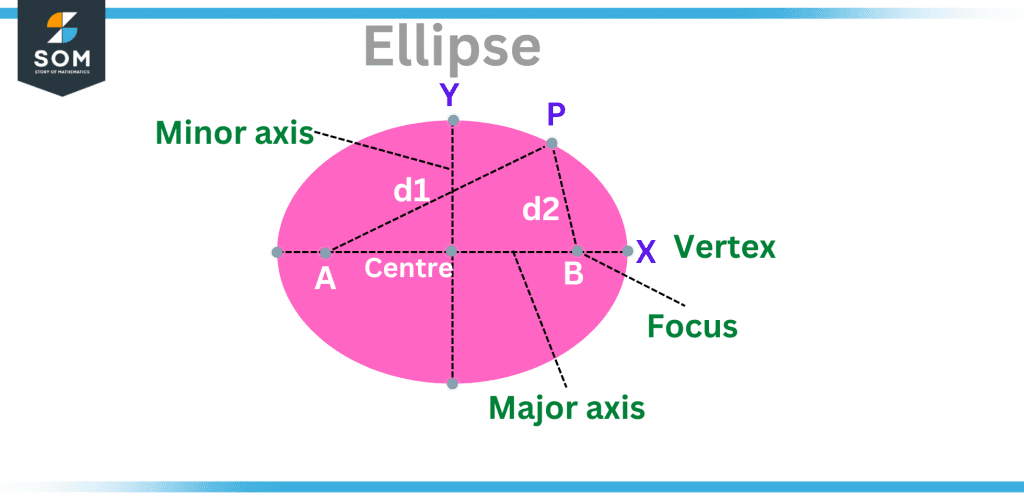
Figure 1 – Labeled components of ellipse.

Equation of Ellipse

The general ellipse equation is used to represent an ellipse in the coordinate plane algebraically. An ellipse’s equation is as follows:

\[\frac { ( x-u )^2 } { a^2 } + \frac { ( y-v )^2 } { b^2 } = 1 \]

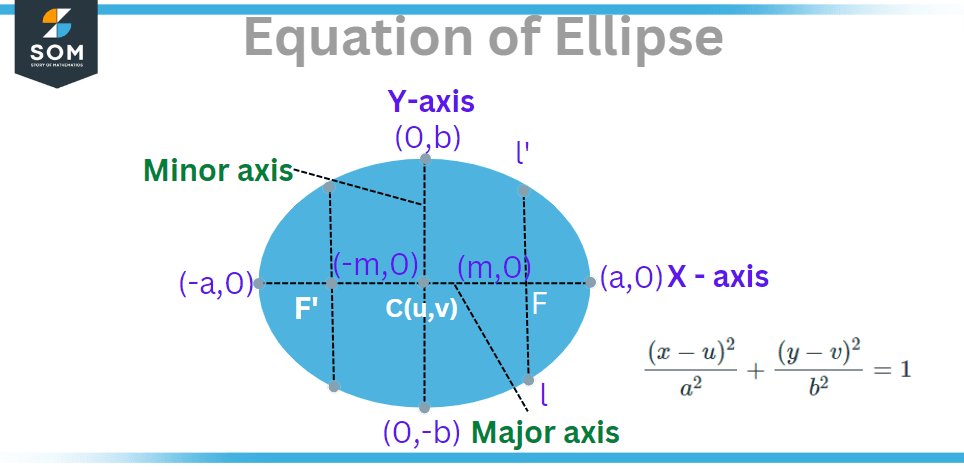
Figure 2 General Equation of Ellipse with centre offset.

Ellipse Standard Equation

The ellipse has two standard equations. These equations are built around the transverse and conjugate axes of each ellipse. The transverse axis is the x-axis in the standard ellipse equation $\frac {( x-u )^ 2 } { a ^ 2 } + \frac { ( y-v ) ^ 2 } { b ^ 2 } = 1 $ and the conjugate axis is the y-axis.

Furthermore, another standard ellipse equation is $\frac { x ^ 2 } { b ^ 2 } + \frac { y ^ 2 } {  a ^ 2 } = 1 $,  with the transverse axis as the y-axis and the conjugate axis as the x-axis. The image below depicts the two standard forms of ellipse equations.

Figure 3 – Standard Equation of Ellipse where the conjugate axis is defined on the y-axis and the transverse axis is defined on the x-axis.

Figure 4 – Standard Equation of Ellipse with the transverse axis as the y-axis and the conjugate axis as the x-axis.

Ellipse Components

Let’s review some key terms related to the various parts of an ellipse.

• Focus: The ellipse has two foci, which have the coordinates F(c, o) and F’ (-c, 0). Thus, the distance between the foci is equal to 2c.
• Center: The ellipse’s center is where the major and minor axes meet.
• Major Axis: The end vertices of the ellipse are (a, 0), and (-a, 0), with the major axis’ length being 2a units.
• Minor Axis: The end vertices of the ellipse are (0, b) and (0, -b), respectively, and the minor axis’ length is 2b units.
• The Latus Rectum: A line drawn perpendicular to the ellipse’s transverse axis is known as the latus rectum and passing through its foci.  The ellipse’s latus rectum length is $ 2b^2 /a $.
• Transverse Axis: The axis that runs through the middle of the ellipse and between its two foci is known as the transverse axis.
• Conjugate Axis: The ellipse’s axis at a point equally spaced from the foci, which is perpendicular to the transverse axis.
• Eccentricity (e<1): A non-circular ellipse’s eccentricity is always greater than zero but less than one.

Ellipse Characteristics

There are several characteristics that help distinguish an ellipse from other similar shapes. These ellipse properties are as follows:

• When a plane crosses a cone at its base angle, an ellipse is formed.
• Each ellipse has two focal points. Any two points on the ellipse have a fixed sum of their respective distances.
• There are major and minor axes on every ellipse, a centre, and eccentricity values that are less than one.

How Do You Make an Ellipse?

There are specific steps to drawing an ellipse in math. The following is a step-by-step procedure for drawing an ellipse of given dimensions.

1. Because the major axis is the ellipse’s longest diameter, determine its length.
2. Draw one horizontal line the length of the major axis.
3. Using a ruler, mark the midpoint. The major axis length is divided by two to achieve this.
4. Using a compass, draw a circle of this diameter.
5. Determine the length of the minor axis, which is the ellipse’s shortest diameter.
6. Now, take the protractor and place it at the midpoint of the major axis. Make a mark at 90 degrees. Swing the protractor 180 degrees and mark the location.At its midpoint, the minor axis can now be drawn between the two marks.
7. Using a compass, draw a circle of this diameter, just as we did for the major axis.
8. Using a compass, divide the circle into twelve 30-degree sections.
9. From the inner circle, make horizontal lines (but not for the major and minor axes).
10. They run parallel to the main axis and radiate outward from all intersections of the inner circle and the 30-degree line
11. Draw the lines a little shorter near the minor axis and a little longer as you get closer to the main axis
12. From the outer circle make vertical lines (but not for the minor and major axes).
13. These run parallel to the small axis and inward from all points where the outer circle and 30-degree lines meet.
14. Make the lines near the minor axis a little longer. but a little shorter as you approach the main axis.If the horizontal line is too far, take a ruler and stretch it slightly before drawing the vertical line.
15. Use your best freehand drawing skills to draw the curves between the points.

Ellipse Graph

Let’s look at a graphical representation of an ellipse using the ellipse formula. To graph an ellipse in a cartesian plane, certain steps must be taken.

Step 1

Crossing with the coordinate axes, the ellipse intersects the x-axis at A (a, 0), A'(-a, 0), and the y-axis at B(0,b), B’ (0,-b).

Step 2

The ellipse’s vertices are A(a, 0), A'(-a, 0), B(0,b), and B'(0,b) (0,-b).

Step 3

Because the ellipse is symmetric about the coordinate axes, It has two foci  S'(-ae, 0), S(ae, 0), and two equation-based directories d and d’ $ x = \frac { a } { e } $ and $ y = \frac {b } {e} $, respectively. Every chord is bisected by the origin O.As a result, origin O is the centre of the ellipse. As a result, it has the shape of a central conic.

Step 4

A closed curve is an ellipse that completely fills the rectangle.

Step 5

The major axis is the segment AA′ of length 2a, and the minor axis is the segment BB′ of length 2b. The major and minor axes are referred to as the ellipse’s principal axes.

Example Ellipse

If the length of an ellipse’s semi-major axis is 10 cm and its semi-minor axis is 8 cm. Determine its location.

Solution

Given the length of an ellipse’s semi-major axis, a = 10 cm, and the length of its semi-minor axis, b = 8 cm, we can calculate the area of an ellipse using the formula:

Area = $\pi$ x a x b

Area = $\boldsymbol\pi$ x 10 x 8 = 80 x $\pi$

Area = 80 x 22/7 = 251.4286 cm$\mathsf{^2}$ area

All images/mathematical drawings were created with GeoGebra.

Elimination Definition < Glossary Index > End Point Definition