Endpoint|Definition & Meaning

Endpoints are where the line segment terminates, with the numbers of a line segment happening between the segment’s two endpoints. As a result, a simple line has no endpoint, a ray has only one, and a line segment contains precisely two. 

Using Endpoints to Name Objects

Endpoints can name several geometric objects, such as horizontal lines, angles, polygons, etc. We can see it in figure 1 below:

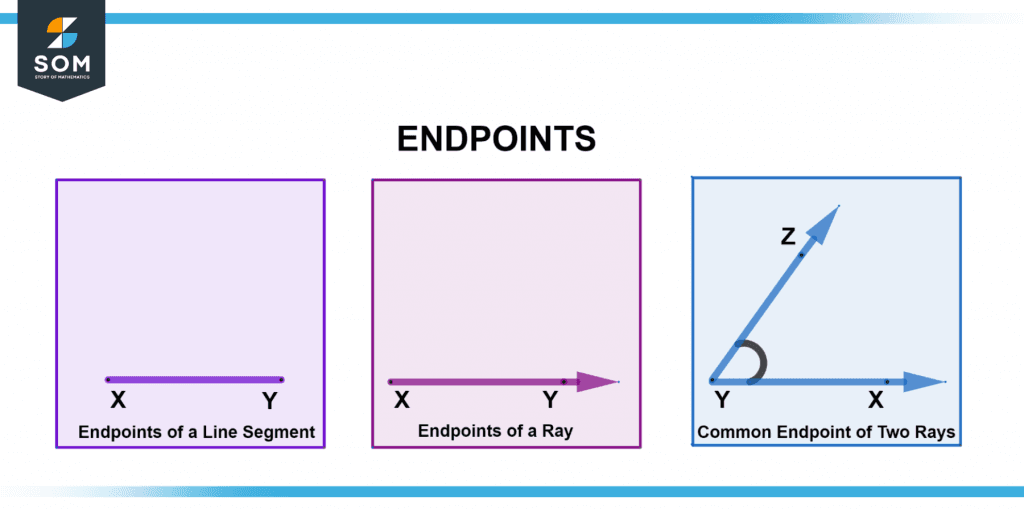
Figure 1 – Endpoints used in naming.

Positions X and Y are the line segment’s ends. The ends of the line segment, XY or YX, are used to identify it. A ray, on either hand, only has one terminal, as seen below. The ray is called with the initial letter of its destination, XY.

As seen above, an angle may be labeled using the common terminal of the two rays. Rays XY and YZ are connected by endpoint Y and create an angle.

The angle can be denoted by the letters $\angle XYZ$ or $\angle Y$ if just its endpoint is used.

Line Segment 

The line segment is a line with two endpoints and a fixed length. It is distinct from a line in that it has no beginning or ending point and can be extended in both directions.

A line is a quantifiable path that connects two points. Line segments have a defined length and may be used to build the edges of any polygon. The illustration below shows a horizontal line XY, with a length corresponding to the distance between its endpoints, X and Y.

Figure 2 below shows a line segment with endpoints.

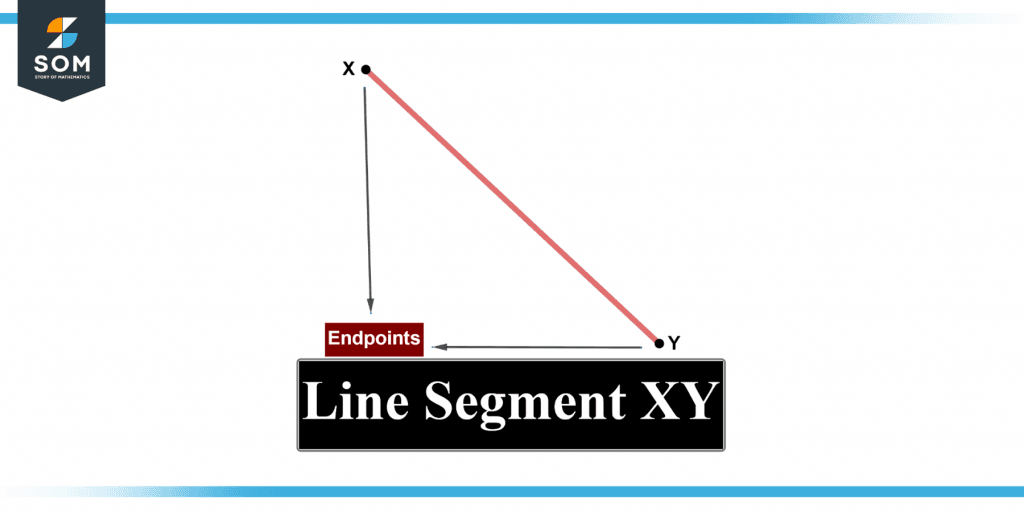
Figure 2 – Line Segment with endpoints.

Ray

A ray begins at a particular location and continues in a specific direction indefinitely. The spot where the beam starts is referred to as the endpoint (confusingly). It may travel through one or so other points on its path to infinity. A ray begins at a point and stretches in one direction indefinitely. As a result, it only has one terminus.

Two Rays

Two rays intersect and make an angle. The vertex of the angle is indeed the place where two rays intersect. The two rays represent the angle’s sides. Two rays collide at the same point to make an angle.

An angle’s vertex is the point at which the rays cross. The two rays represent the angles’ sides. Rays are used to depict angles. When two rays connect, an angle is generated. The vertex connects the two rays and also acts as their starting point. The angle is composed of two rays known as the angle’s arms. Consequently, the vertex is the point at which the two rays intersect.

Endpoint Formula

The endpoint formula helps find the values of endpoints in a line segment or ray. Endpoints are the spots on a reference line and one point on a ray when both the line and the ray ends. The line doesn’t continue beyond the ends. The midpoint formula is required to compute the endpoints. The midpoint is the center or midway point of any line connecting the ends.

Letting (Xm, Ym) be the midpoint of a line connecting two locations X (X1, Y1) & Y (X2, Y2). We can solve for either endpoint using the midpoint formula.

Figure 3 below shows the endpoint formula.

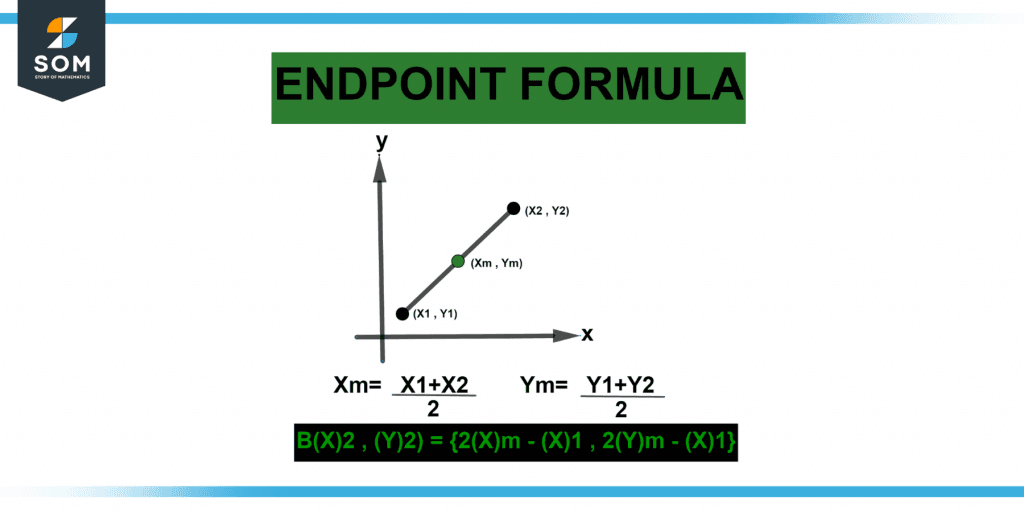
Figure 3 – Representation of the Endpoint formula

Examples of Endpoint 

Below are some endpoint examples.

Example 1

M(4, 3) is the union of line A(2, 5) and B in Example 1. (x, y). Determine B’s coordinates using the endpoint formula.

Solution

First, make a note of the values Xm=4, Ym=3, X1=2, and Y1=5.

Now that we have the formulae for the endpoints,

(BX2 , Y2) equals {2Xm – X1 , 2Ym – X1}

By the formula for X2 = 2Xm – X1

Putting the values in the formula:

X2 = 2(4) – 2

X2 = 8-2

Now by performing subtraction, we get: 

X2 = 6

By the formula for Y2 = 2Ym – Y1

Putting the values in the formula:

Y2 = 2(3) – 5

Y2 = 6-5

Now by performing subtraction, we get:

Y2 = 1

x = 6, y = 1

As a result, the parameters of B(x, y) Equals (6, 1) imply that x = 6 and y = 1.

Example 2

C denotes the middle of a 5-degree radius circle (8, 9). On just this circle, a radius is marked with one of its vertices (2, 4). Using the endpoint formula, get the opposite endpoint of the diameter.

Solution

Note the numbers Xm Equal 8, Ym Equal 9, X1 Equal 2, & Y1 Equal 4.

The method to find the endpoints, as we already know, is

(BX2 , Y2) equals {2Xm – X1 , 2Ym – X1}

By the formula for X2 = 2Xm – X1

Putting the values in the formula:

X2 = 2(8) – 2

X2 = 16-2

Now, applying subtraction, we obtain:

X2 = 14

By the formula for Y2 = 2Ym – Y1

Putting the values in the formula:

Y2 = 2(9) – 4

Y2 = 18-4

Now by performing subtraction, we get:

Y2 = 14

x = 14, y = 14

Consequently, the parameters B(x, y) Equals (14, 14) indicate that x = 14 and y = 14.

Example 3

M(8, 5) represents the junction of lines A(3, 4) and B. (x, y). Determine B’s coordinates using the endpoint formula.

Solution

First, make a note of the data Xm equal 8, Ym equal 5, X1 equal 3, and Y1 equal 4.

As we already know, the formula for the endpoints is: 

(BX2 , Y2) equals {2Xm – X1 , 2Ym – X1}

By the formula for (X)2 = 2Xm – X1

Putting the values in the formula:

X2 = 2(8) – 3

X2 = 16-3

Now by performing subtraction, we get:

X2 = 13

By the formula for Y2 = 2Ym – Y1

Putting the values in the formula:

Y2 = 2(5) – 4

Y2 = 10-4

Now by performing subtraction, we get: 

Y2 = 6

x = 13, y = 6

As a result, the B(x, y) Equals (13, 6) parameters suggest that x = 13 and y = 6.

All Images are made using GeoGebra.

Ellipse Definition < Glossary Index > Equal Definition