Equal|Definition & Meaning

We need to “equate” or show equality between two values in math, the equal sign is the sign that shows equality between two instances. Hence, the equal sign in mathematics expresses equality between the equations, values, or expressions written on both sides. 

The symbol for the equal sign is shown below.

Figure 1 – Equal Sign Symbol

Equal Sign in Maths

In mathematics, there are several situations where the equal sign is used, such as defining a statement of fact in a distinctive matter, writing definitions, words with conditions, or defining a universal equivalence. We put the ‘equal to’ sign between two things that are the equal or same.

Figure 2 – Example of Equal

A very important thing to be noted about the equal sign is that an equation cannot be expressed without an equal sign otherwise it can not be an equation.  The symbol “=” shows that whatever is on the left side of the sign is exactly the same quantity or value as whatever is on the right of the sign.

Some examples are equal are given below:

3 + 7 = 10

(y+ 3)$\mathsf{^2}$ = (y$\mathsf{^2}$ + 9+ 6y)

4 – 1 = 3

Use of ‘Equal To’ Sign in an Equation

An equation, typically, contains constants, variables, and an equal to sign in the form of an expression. In every equation, the expression on the right-hand side (RHS) is equal to the expression on the left-hand side (LHS).

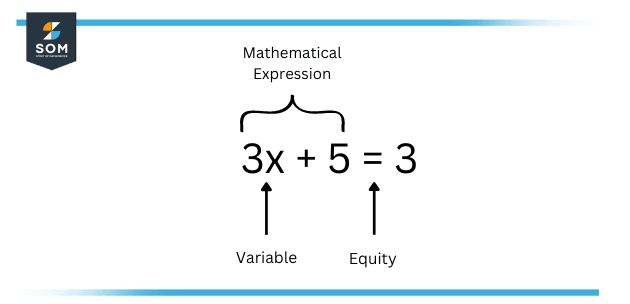
FIgure 3 – Equity in Equation

Basic Properties of Equation

The Basic Properties of the Equation are listed below:

1. Substitution property: For any given values x and y and any given expression F(x), if x = y, then F(x) = F(y) (given that both sides are well-formed). Some specific examples are:a) For any real numbers a, b, and c, in the event that a = b, then a + c = b + c.

   b) For any real numbers a, b, and c, in the event that a = b, then a − c = b − c.

   c) For any real numbers a, b, and c, in the event that a = b, then ac = bc.

   d) For any real numbers a, b, and c, in the event that a = b and c is a non-zero, then a/c = b/c.

2. Reflexive property: For any value of a, a = a.
3. Symmetric property: For any values of a and b, if a = b, then b = a.
4. Transitive property: For any values of a, b, and c, if a = b and b = c, then a = c.

The above three properties justify equality as an equivalence relation. They were initially counted among the Peano axioms for natural numbers. Although the symmetric and transitive properties are usually looked at as elemental, they can also be deduced from the properties of substitution and reflexive.

Symbols Related To Equality

Following are the symbols that are associated with equality,

Not Equal To ($\neq$)

As the sign suggests, the not equal symbol in math means that the two expressions are not equal to each other. The symbol is used like this:

4 $\neq$ 3

Equivalent ($\equiv$)

The equivalent sign is used in modular arithmetic to show that two given numbers are congruent modulo any number N. Generally, the equivalent symbol is used in an expression like this:

x $\equiv$ y(mod N)

Approximation ($\approx$)

The approximate symbol shows that the two values are approximately the same to each other. Generally, the symbol is used in an expression like this:

$\pi\approx$ 3.14

Congruent ($\cong$)

The ≅ (congruent) symbol in geometry is utilized to show that two shapes are identical to each other in size and shape. Generally, the congruent symbol is used in an expression like this:

$\bigtriangleup$ ABC $\cong\bigtriangleup$ DEF

Less Than or Equal To ($\leq$)

It means a number is either equal to or less than another number. it can also be defined as no more than, at most, not exceeding, and a maximum of.

3 $\leq$ 3

Greater Than or Equal To ($\geq$)

It means that the number is either equal to or greater than a certain value. It is used to show that one number is greater, in any sense, than the other number. ‘is equal’ term shows that two numbers are equal. At the point when these phrases are joined with one another, they make another phrase, “Greater Than Or Equal To.” This phrase is used to express that the quantity or amount value could actually be equal to or greater than the given limit.

4 + 3 $\geq$ 3

Equity in Equations

To find the values of some variables, called unknowns, an equation is used, for which the specified equality is true. The term “equation” may also direct to an equality relation that is satisfied exclusively for the values of the variables that one is keen on. For example, x$\mathsf{^2}$ + y$\mathsf{^2}$ = 1 is the equation of the unit circle, which means the radius of the circle is equal to 1.

Examples

Let’s take a look at the examples given below to get a grip on the topic and to understand the different cases where we can use equal signs:

• The perimeter of a square is equal to its side length multiplied by 4, i.e., P = 3 x side.
• Distributive property of multiplication over addition: 2(3+4)= (2 x 3) + (2 x 4), this means multiplication 2 with the sum of 3 and 4 is the same as firstly multiplying the numbers 4 times 2 and 4 times 6 and then adding the results.
• Equations in one variable: 2x+14 = 5x + 8
• Equations in two variables: 9x + 4y = 8, 3x – 7y = 18
• Geometry formulas: c$\mathsf{^2}$ = a$\mathsf{^2}$ + b$\mathsf{^2}$

Solved Problems Involving the Equal Symbol

Example

If we suppose mathematically that the total cost of 5 apples is exactly the same as that of 3 oranges, then which sign will best fit?

Solution

It has been explained above that when we compare two quantities, and they are the same, we use the “equal to” sign. So in this scenario, the “equal to” sign is the best fit:

Cost of 5 apples = Cost of 3 oranges.

All images/mathematical drawings were created with GeoGebra.

End Point Definition < Glossary Index > Equality Definition