Equality|Definition & Meaning

A = B indicates the equality of A and B, which is also pronounced as A = B. The “equals sign” is the symbol “=.” It is claimed that two items are distinct if they are different.

Figure 1 below shows that the number of squares on the left side equals the squares on the right side. 

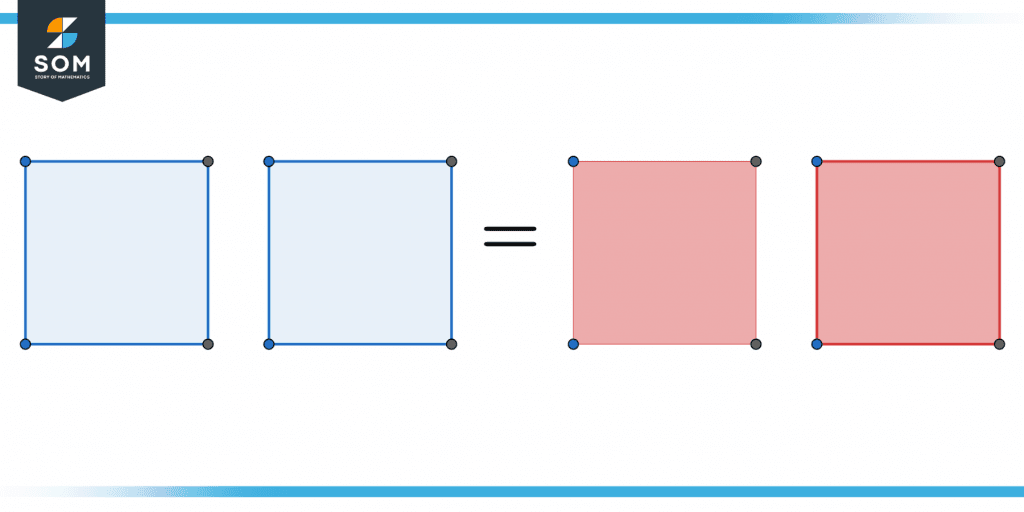
Figure 1 – Representation of equality using shapes.

Properties of Equality

Below are several properties of equality.

Addition Property 

The addition property of equality states that the calculation still stands true when the same value is added to the right and left sides of an equation. This condition may be formally expressed as follows: when real numbers p, q, and r, if p = q, then p + q = q + r. Equations involving algebra and arithmetic can both leverage this characteristic.

Subtraction Property

The subtraction property asserts that an equation is still valid if the exact real number is removed from both sides of it. For real numbers x, y, and z, the expression for this characteristic may be expressed as x – z = y – z if x = y. This characteristic can be used to resolve algebraic problems.

Multiplication Property 

The multiplication property states that when the two sides of an equation stay equal when the exact real number is multiplied on both by sides at the same rate. The formula for this condition may be written as follows: for real integers x, y, and z, if x = y, then xz = yz.

Division Property

The division property is defined as quality still exists when dividing both sides of an equation by the exact real integer. This condition may be expressed in mathematical terms: given real numbers p, q, and r, if p = q, then p/r = q/r. An algebraic equation’s unknown variable can be located using this characteristic.

Substitution Property

The substitution property states that if x = y for any quantity a and any expression F(x), then F(x) = F(y) (provided that both sides are well-formed).

Here are a few particular instances:

• If any real number x = y, then x + z = y + z follows (in this case, F(x) is x + z).
• If x = y for any real number x, y, and z, then x z = y z (in this case, F(x) is x z) follows.
• If x = y for any real number x, y, and z, then xz = yz (in this case, F(x) equals xz).
• If x = y for any real number a and c is not zero, then x/z = y/z (in this case, F(x) is x/z).

Reflexive Property

The Reflexive property of equality is defined as a quantity that is always equal to itself. x = x for any value of x.

Symmetric Property

The symmetric property of equality is fairly straightforward. In other words, the equation still makes sense even if two equations’ sides are switched. If any two quantities, x and y, are equal, then y and x are also equal.

Figure 2 below shows the symmetric property of equality, where the area of the square on the left side is equal to the area of the polygon on the right side.

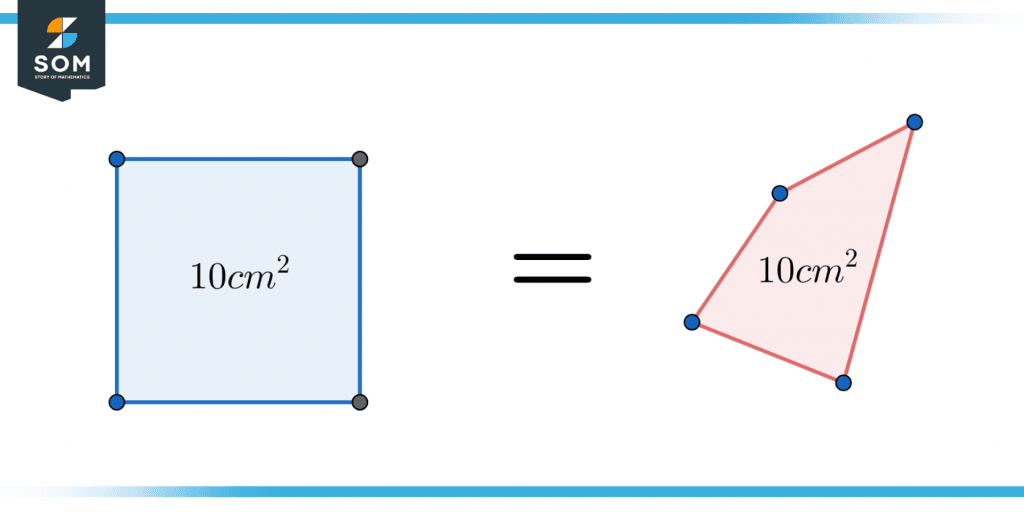
Figure 2 – Representation of the symmetric property of equality.

Transitive property 

The transitive property of equality states that If x = y and y = z for any quantities x, y, and z, then x = z.

Equality as Predicate

A predicate is an expression comprising one or more variables defined on a particular domain. Giving the variable a value or quantifying it can turn a predicate with variables into a proposition. Here are a few examples of predicates: Let x = y be denoted by E(x, y).

Equality is a statement that may be valid for some values and untrue for other values when A and B are not fully described or rely on some factors. The predicate equal is a binary relation with two parameters that might result in a truth value (false or true). Its calculation from the two variables is a comparison in computer programming.

Identities

When a binary operation is conducted on a set, the identity element (also known as a neutral element) is an element of the set that leaves each element of the set untouched. In algebraic structures like groups and rings, this idea is applied. 

A = B denotes that A and B define the same function when A and B can be considered functions of some variables. Sometimes, an identity is used to describe such equivalence of functions. An illustration is:

(x+1)(x+1) = x$\mathsf{^2}$+2x+1

Approximate Equality

Approximate equality is frequently utilized in engineering and physics, but it is also employed occasionally in mathematics. When two quantities have sufficiently similar values and have little practical difference, they are about equivalent.

Even if it were more clearly defined, the transitive property of the binary relation “is about equal” (denoted by the symbol $ \approx $) between real numbers or other items is that it does not include the inverse (because a lot of little things may build up to something significant). But equality is essentially transferable everywhere.

The following figure represents how approximate equality is used:

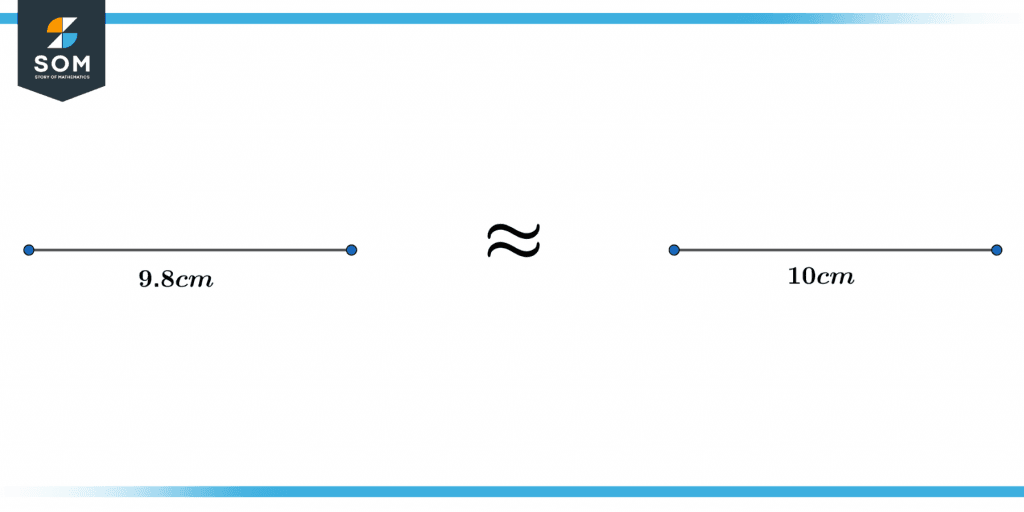
Figure 3 – Representation of approximate equality.

Examples of Equality

Here are some examples of equality that will help you clear the concept further.

Example 1

While working on his school homework, a student needs to solve the given equation: 

x – 3 = 7

Using the subtraction and addition property of equality, find the value of x.

Solution

To solve this equation, we have to add three on both sides to cancel out three on the left side of equality. Then by adding three on both sides, x = 10. 

Example 2

While teaching, a professor asks his students to solve the following expression:

6x = 36

Using the multiplication property and division property of equality, solve the equation to get the value of x.

Solution

To solve this expression, we must divide six by both sides of the equality to cancel out the six on the left side. Then by dividing six by both sides, x = 6.

All Images/Tables are made using GeoGebra.

Equal Definition < Glossary Index > Equation Definition