Equation|Definition & Meaning

It illustrates the mathematical equivalence of one expression with another expression and helps in finding the value of an undetermined variable.

Illustration of Equation 

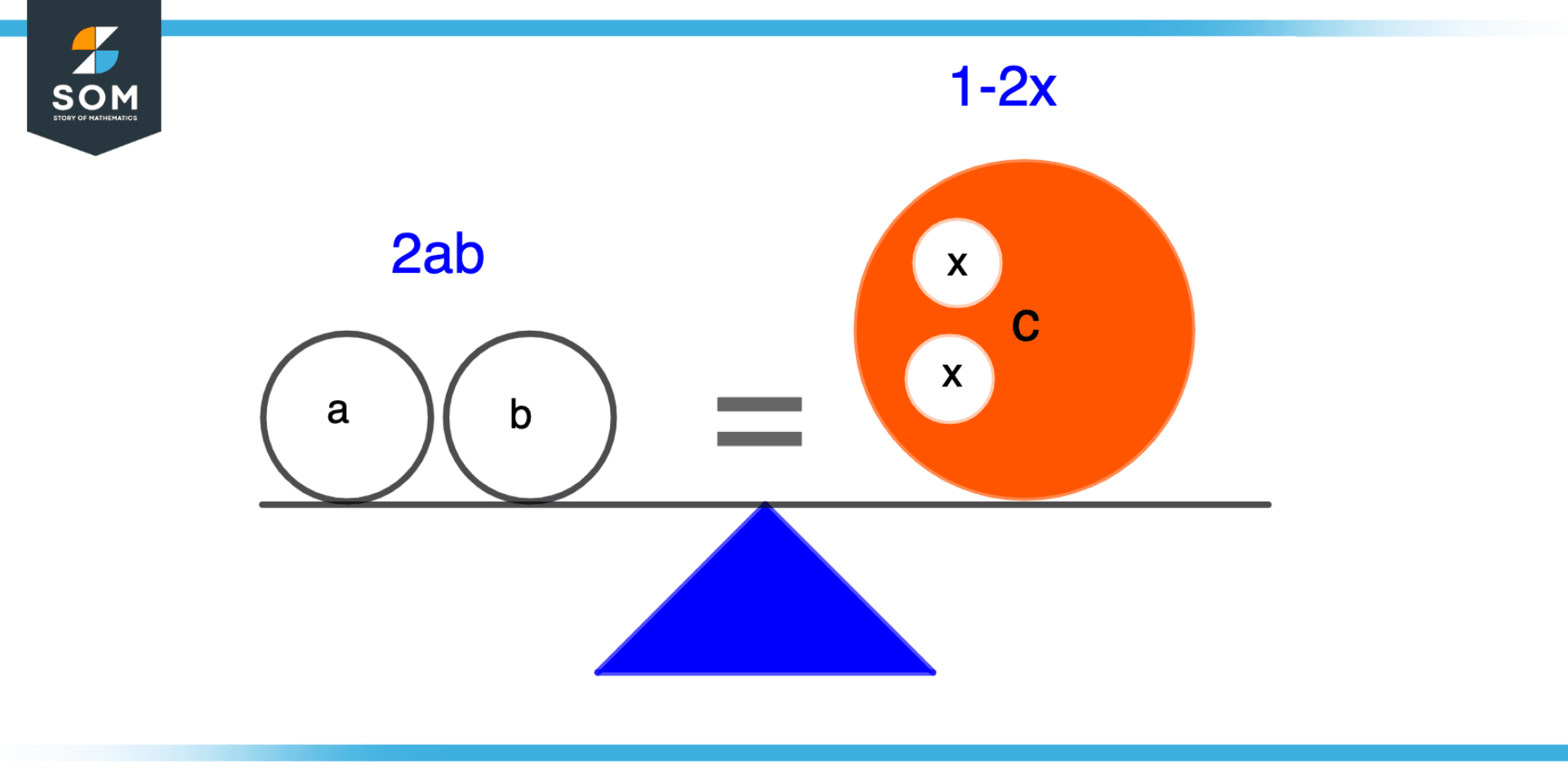
Figure 1 – Illustration of Equation

Suppose an equation as a weigh beam or scale, we know that the weigh beam has two sides and there is a center in between these sides, treat the center as an equality sign and suppose there are a and b quantities on the left side and right side and c quantity on the right side. Consider them as weight, in order to have the equivalency between the left and right portions as shown in the figure we have to make a balance between the two sides by either adding weight or removing weight. 

When we are able to balance the two sides we can take this scenario as an analogy to the equation where the left side represents one mathematical expression and the right side represent another expression while the center of the weighing beam is equality which gives the mathematical equivalence between two sides. This concept is illustrated in the figure above.

Components of Equations

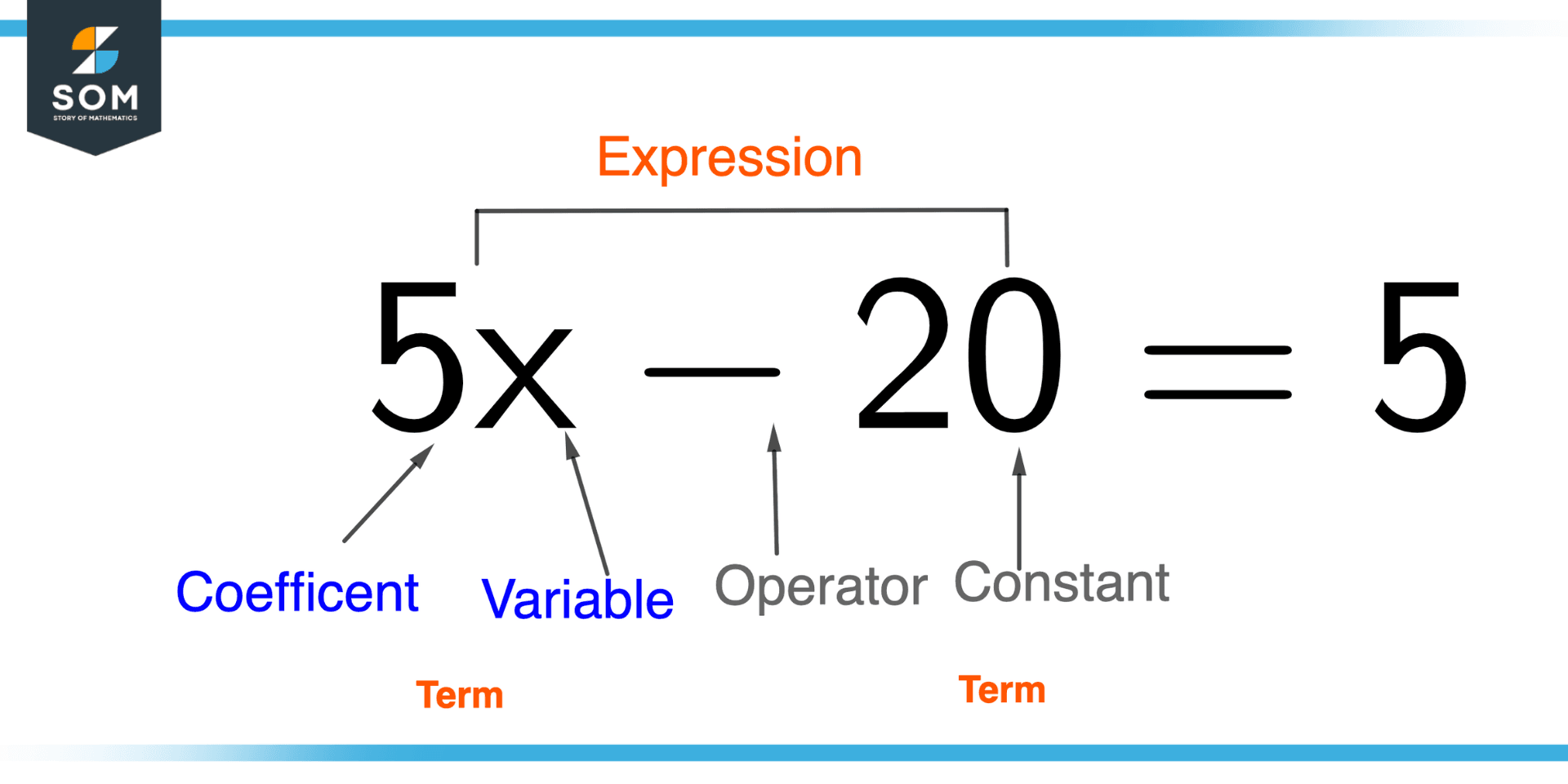
Figure 2 – Component of equation

There are various components that makeup and equations.

Coefficient

Mathematicians use coefficients to multiply terms in polynomials, series, and expressions; they are usually numbers. It is also known as the factor of multiplication.

Variable

Symbols and placeholders are used to represent mathematical objects in mathematics. There are various types of variables, including numbers, vectors, matrices, functions, arguments, sets, and elements.

Operator

Mathematical operators are symbols that indicate how an operation will be carried out. For instance addition, subtraction, division, and multiplication.

Constant

Typically, mathematicians refer to mathematical constants by their names or symbols (e.g., alphabet letters) that are unambiguous in their meaning, enabling them to be used across a variety of mathematical situations without changing their values.

Expression

An expression is the amalgam of coefficient, variable, constant and mathematical operator without an equality sign.

All the components of the equations are shown in the figure above.

Categories of Equations

Although there are many types of equations, we generally divide them into three categories:

1. Linear Equations
2. Quadratic Equations
3. Cubic Equations

Linear Equation

An equation of first order is a linear equation. A linear equation in a coordinate system is defined by lines. We can define a linear equation in one variable as the equation containing only one homogeneous variable of degree 1.

There is no restriction on either using one variable or many in a linear equation. It is called linear equations in two variables, and so on, if there are two variables in the linear equation. For instance, 3y = 2x + 4 and 5x – 3y + 9 = 0 are linear equations.

Quadratic Equation

Approximately a quadratic equation is a polynomial equation that has a degree of 2, such as f(x) = Lx² + Mx + N = 0 where L, M, and N belong to real numbers. The so-called leading coefficient L is used to denote the leading term of f (x), and the absolute term N is used to denote the absolute term.

L is defined as a positive quadratic equation when its roots satisfy its equation (α, β). Two roots are always present in the quadratic equation. In addition to real roots, imaginary roots can also exist. Adding a zero to quadratic polynomial results in a quadratic equation. The values of L that satisfy the quadratic equation are roots.

Cubic Equation

Mathematicians express cubic equations with the cubic equation formula. The term cubic equation refers to an equation with degree three. The roots of cubic equations are 1 real and 2 imaginary or 3 real roots. In mathematics, cubic polynomials are polynomials with three degrees. The cubic equation is written as

ax³ + bx² + cx = d = 0

Comparison of Equation With Expression

Properties of Equations

1. An equation is represented by an equality sign placed between two mathematical expressions to show the mathematical equivalence.
2. The equal sign is mandatory for equation representation.
3. Undetermined values can be computed with equations. For instance, 2x + 3x + 2 = 0 has the solution x = -2/5.

Properties of Expression

1. Unlike equations, expression is represented by just a mathematical expression without the “=” sign.
2. There is no equality sign in the expression, it contains only the variable, coefficient, mathematical operator, and constant.
3. The expression can only be simplified further and doesn’t provide knowledge to determine unknown quantities. For instance, 2x + 4; we cannot compute x.

Illustration of Important Equations

Equation of a Simple Line

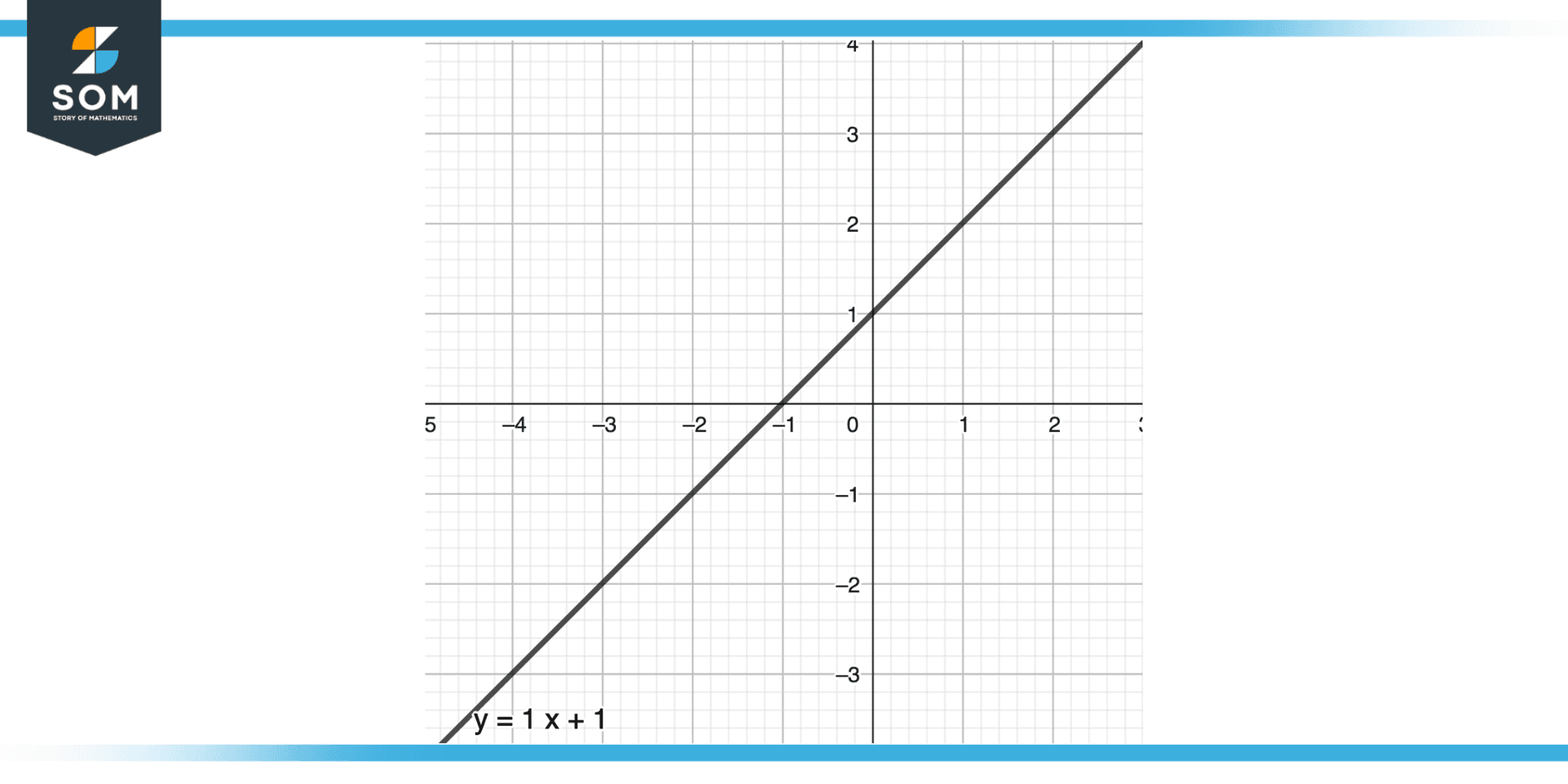
Figure 3 – Equation of line

The equation of a simple line ax + by + c = 0 can be represented as slope intercept form as:

y = mx + c

Where m is the slope.

Equation of X-axis

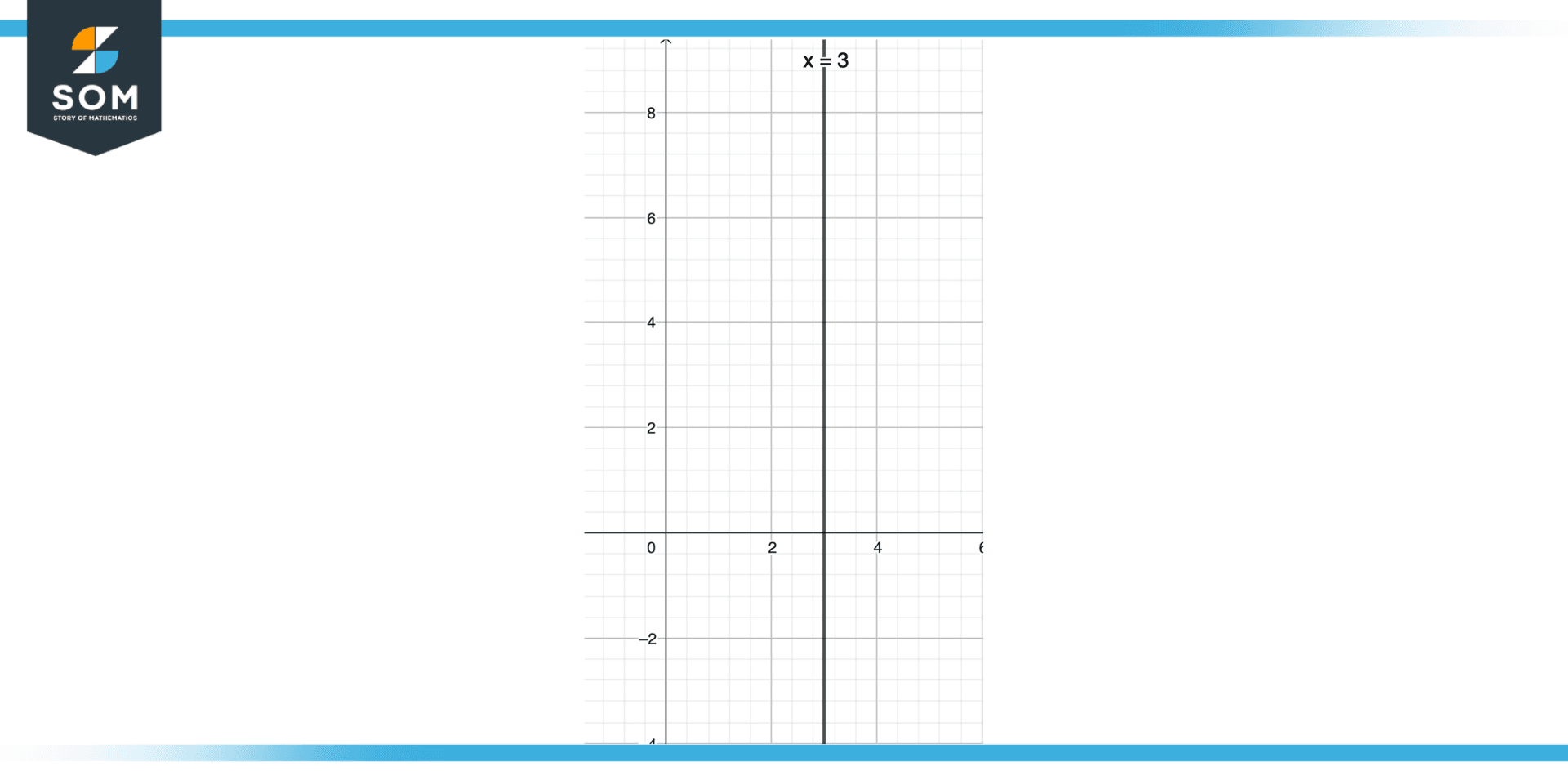
Figure 4 – Equation of the x-axis.

For the x-axis equation, we will use the standard form of the equation of the line which is y = mx + c. We know that, at the x-axis, y = 0. Putting y = 0 in the above equation gives the equation of the x-axis as:

x = c or y = 0

Equation of Y-axis

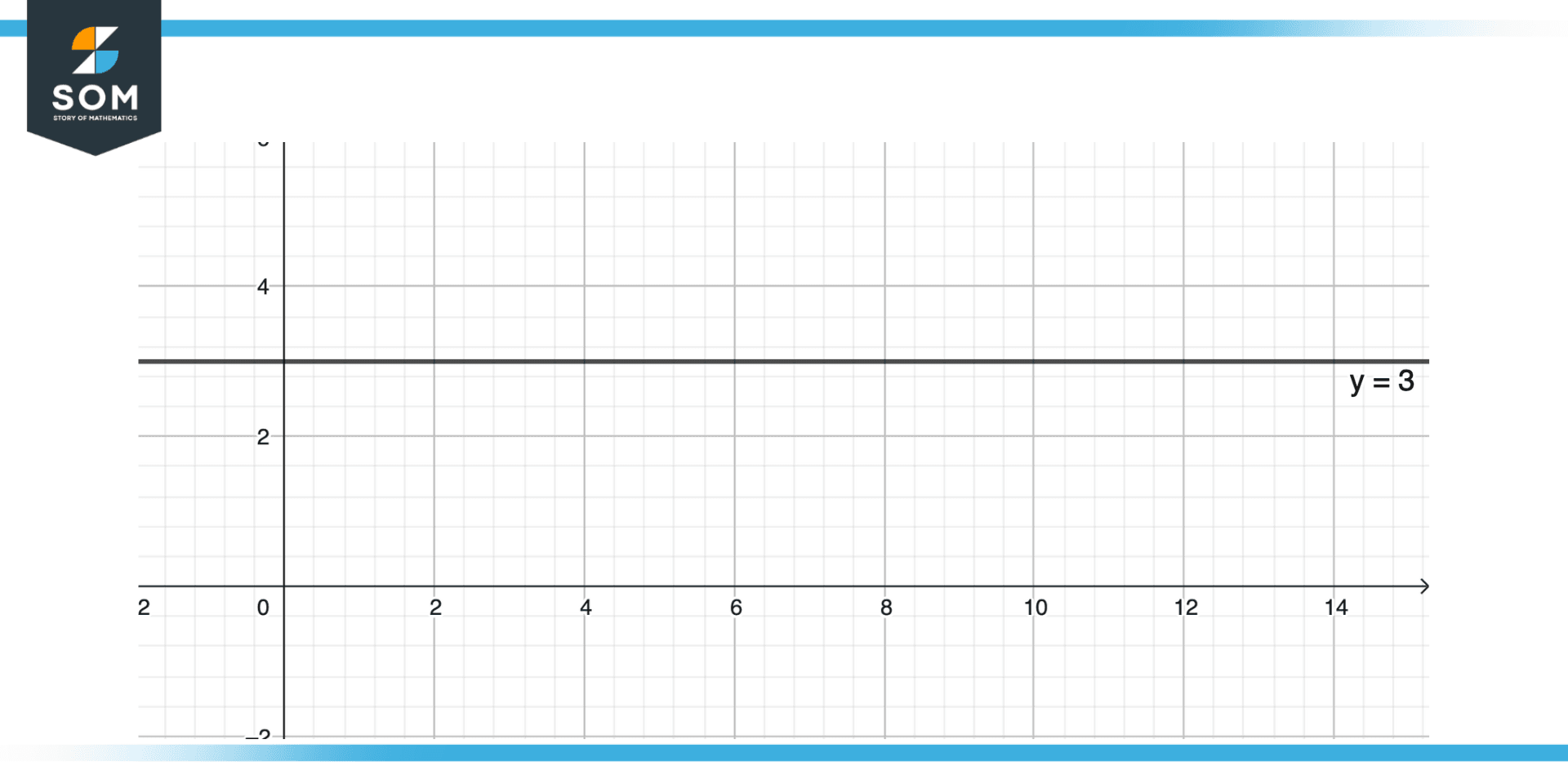
Figure 5 – Equation of y-axis.

For the y-axis equation, we will use the standard form of the equation of the line which is y = mx + c. We know at the y-axis x=0 so putting x=0 in the above equation gives the equation of the x-axis as:

y = c  or  x = 0  

Examples of Equations

Example 1

Consider two equations: 2x+4y=2 and 2x+3y=1. Compute the unknown value of x and y.

Solution

2x + 4y = 2  [Eq. 1]

2x + 3y = 1  [Eq. 2]

Subtracting equations 1 and 2 gives:

2x + 4y = 2

-2x – 3y = 1

y = 1

Put the value of y in equation 1:

2x + 4(1) = 2

2x + 4 = 2

2x = 2 – 4

2x = -2

x = $\mathsf{\dfrac{-2}{2}}$

So, x=-1 and  y=1.

Example 2

Consider two equations x²-16=0 and x²+6x=0. Solve for the value of x.

Solution

Equation 1

x² – 16 = 0

x² = 16

Taking square root on both sides:

\[ \mathsf{\sqrt{x^2} = \sqrt{16}} \]

x = $\pm$4

Verify by putting the value of x in the original equation:

x² – 16 = 0

4² – 16 = 0

16 – 16 = 0

Equation 2

x² + 6x = 0

Taking x as common:

x(x + 6) = 0

It implies that:

x = 0

x = -6

Verify by putting the value of x in the original equation:

(-6)² + 6(-6) = 0

36 – 36 = 0

All mathematical drawings and images were created with GeoGebra.

Equality Definition < Glossary Index > Equiangular Triangle Definition