Equiangular Triangle|Definition & Meaning

Let us first develop a fundamental understanding of triangles and their various types before learning about equiangular triangles. A triangle is a kind of polygon that is composed of three sides, and its vertex is formed by joining two of its sides together. In a triangle, when any of its two sides meet at a vertex an angle is created between them. One of a triangle’s most significant characteristics is that its internal angles add up to 180 degrees. This characteristic of a triangle is known as the angle sum characteristic. 

Classification of Triangles

We can categorise triangles based on the measure of their interior angles and dimensions of their sides.

Types of a Triangle According to Its Sides

• A triangle whose measure of all three sides is the same is known as an equilateral triangle.
• A triangle whose any two of the three sides are similar in length is known as an Isosceles triangle.
• A triangle whose all sides have varying lengths from each other is known as a scalene Triangle.

Types of a Triangle According to Its Angles

• An acute angle triangle is one with all of its angles being less than 90 degrees.
• Right angle triangles are those that have one angle that is at a right angle such that, 90 degrees.
• Obtuse angle triangles are those that have one angle that is greater than 90 degrees.

Equiangular Triangles

Equiangular triangles are the ones whose measure of all sides and inner angles is the same. Every angle of an equiangular triangle measures 60 degrees, and the total of all the inside angles of this triangle equals 180 degrees.

Another name for this is an equilateral triangle. Linguistically speaking, the name equilateral is the combined form of the terms “equi” and “lateral” and their literal meaning is equal sides. Let us assume there is an equilateral triangle ABC. Then as per its definition mentioned above, its sides “AB”, “BC”, and “AC” are of the same length, such as AB = BC = AC. Similarly, its internal angles ∠A, ∠B, and ∠C are equal, such that ∠A = ∠B = ∠C = 60°.

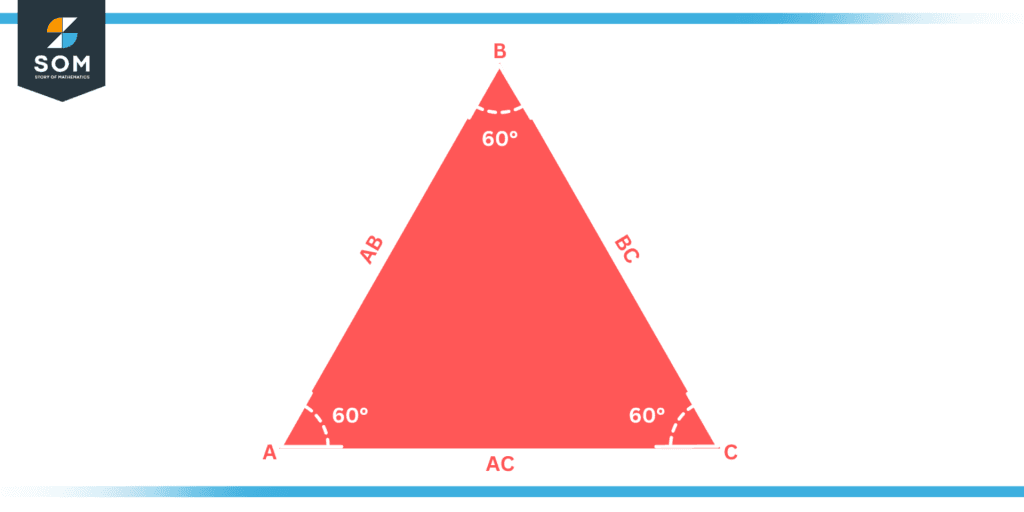
Figure 1: Illustration of Equiangular Triangle

Fundamental Characteristics of an Equiangular Triangle

• An equiangular triangle is a standard polygon, and it has three sides.
• Each of the three sides is equal to the others.
• Each of the three angles is equal and congruent to the others, whereas every angle measures sixty degrees.
• If you draw a perpendicular from any of the vertexes of an equiangular triangle, it will split the opposite side of the vertex into two equal parts. At the same time, the angle of the vertex at which you draw the perpendicular also gets bisected into two equal parts each measuring sixty degrees.
• An equiangular triangle’s circumcentre point and centroid point are identical.
• The median, angle bisector, and altitude for each side of an equiangular triangle are identical.

Area of an Equiangular Triangle

We can define the area of an equiangular triangle as the region or space enclosed by it in a 2D plane. In case the dimension of one side of an equiangular triangle is “s”, you can drive the formula for its area as shown below.

Triangle’s Formula for Area = $\frac{1}{2}\ \times\ base\ \times\ height$

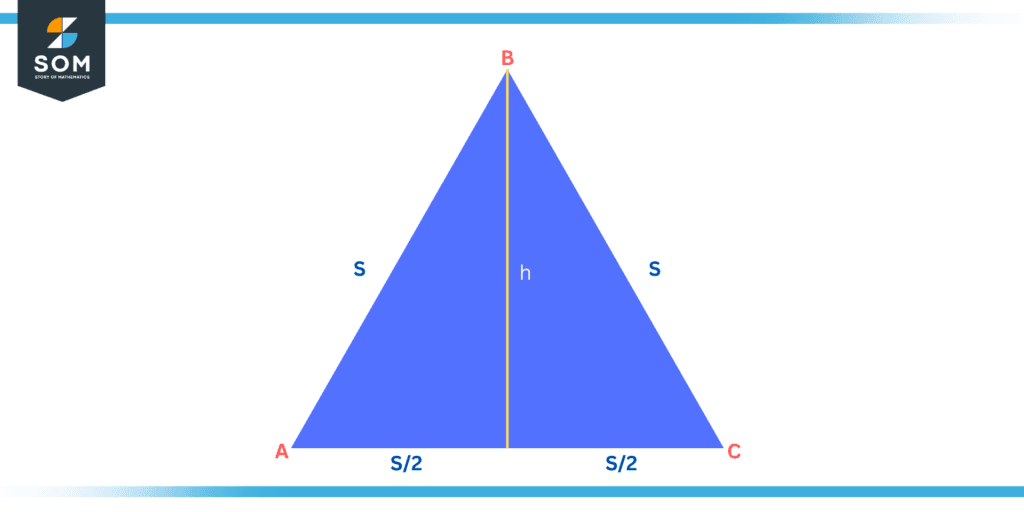
Figure 2: Area of Equiangular Triangle

Now, according to the figure, we can see that the base of the triangle is “s”. We can also observe in the figure that the altitude of the height has divided the equiangular triangle into two identical right-angle triangles. Thus, we can calculate the height “h” using the Pythagoras theorem.

Hypotenuse² = Base² + Height²

s² = $\left(\frac{s}{2}\right)^2+\ h^2$

h² = $s^2\ -\ \left(\frac{s}{2}\right)^2$

h² = $\frac{{3s}^2}{4}$

h = $\frac{\sqrt3}{2}s$

Now put the values of height into the formula of the area as shown below.

Area of an equiangular triangle =$\ \frac{1}{2}\ \times\ s\times\ \frac{\sqrt3}{2}s$

Thus,

Area = A = $\frac{\sqrt3}{4}\ s^2$

Perimeter of an Equiangular Triangle

As we are cognizant of the fact that the perimeter of a triangle is equal to the summation of the lengths of its three sides. Let us assume that the length of one side of an equiangular triangle is “a”. Now, we do know that all sides of an equiangular triangle have the same length. Therefore,

Perimeter of an equiangular triangle = P = a + a + a

Hence,

P = 3a

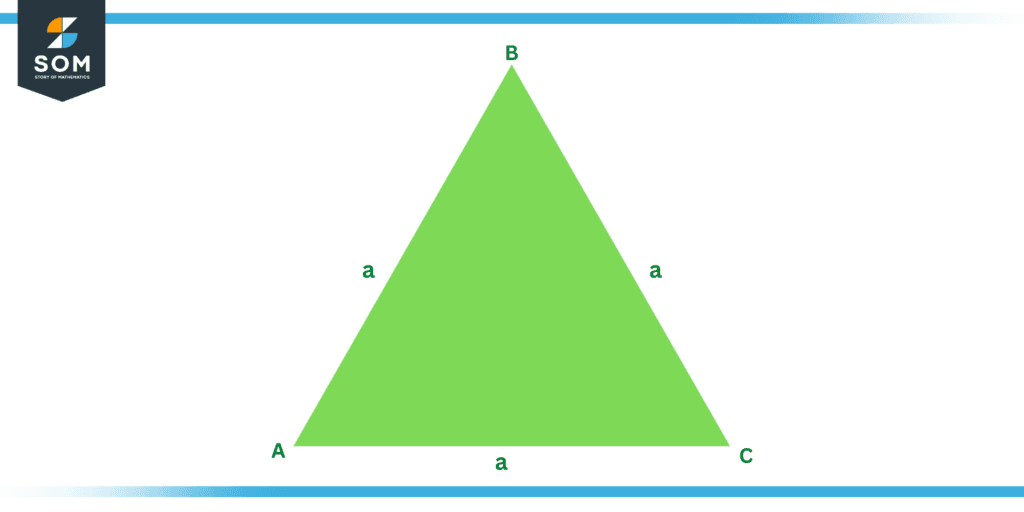
Figure 3: Perimeter of Equiangular Triangle

Centroid of an Equiangular Triangle

Like all the other triangles, the centroid of an equiangular Triangle is located at its centre point. Finding its centroid is relatively simple as all of its sides are identical in length. In order to determine the centroid, draw perpendiculars for every vertex point of an equiangular triangle towards the opposing sides. The centroid will be the location where all of these perpendiculars, which are all of the same lengths, intersect. Below is a diagram of the triangle’s centroid.

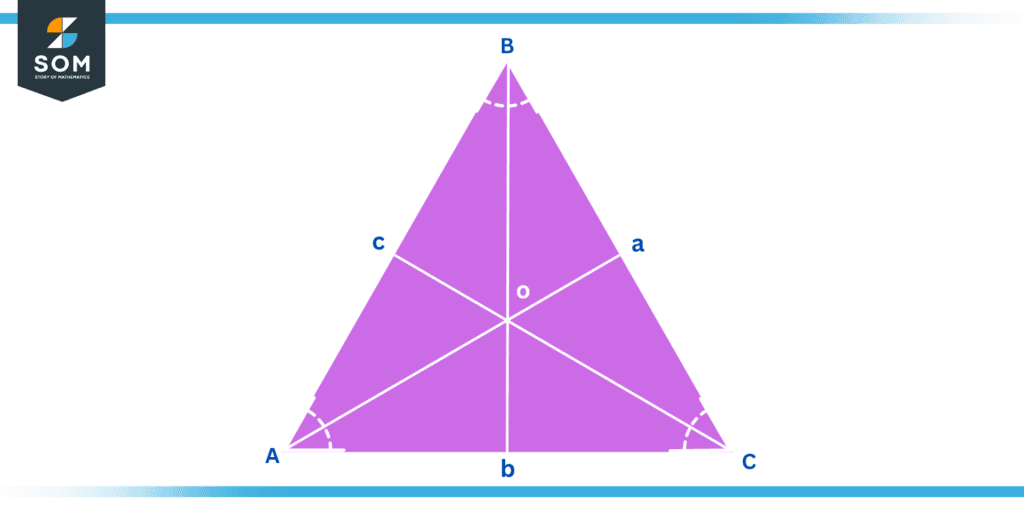
Figure 4: Centroid of Equiangular Triangle

Solved Examples of Equiangular Triangles

Example 1

The length of side AB of an equiangular triangle ABC is 5 cm. Find the perimeter of the triangle

Solution

Perimeter of a Triangle ABC = AB + BC + AC

We also know that all sides of an equiangular triangle are identical, such that

AB = BC = AC

Thus,

Perimeter of an equiangular Triangle ABC = AB + BC + AC

Perimeter of an equiangular Triangle ABC = 5 + 5 + 5

Perimeter of an equiangular Triangle ABC = 15 cm

Example 2

Find the Area of an equiangular triangle ABC whose length of side BC is 2 cm.

Solution

As per the derivation done above,

Area of an equiangular triangle = $\frac{\sqrt3}{4}\ s^2$

Where “s” is the length of any of the sides of an equiangular triangle.

In this case,

s = BC = 2 cm.

Now put the value of s in the formula of area.

Area of equiangular triangle ABC = $\frac{\sqrt3}{4}\ 2^2$

Area of equiangular triangle ABC = $\frac{\sqrt3}{4}\ 4$

Area of equiangular triangle ABC = $\sqrt3$

All images/mathematical drawings were created with GeoGebra.

Equation Definition < Glossary Index > Equidistant Definition