Event|Definition & Meaning

Figure 1 shows the event E and the sample space S in the Venn diagram. 

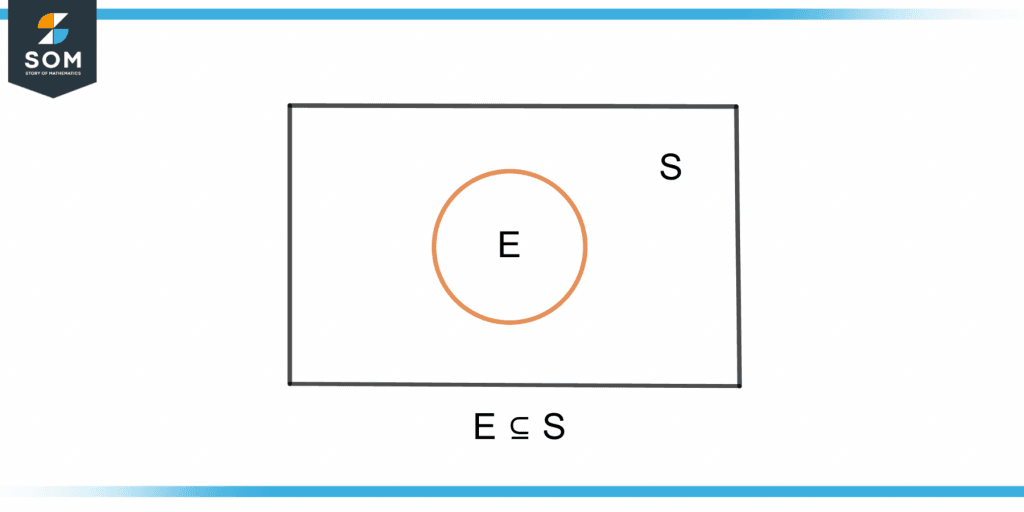
Figure 1 – Venn Diagram of an Event E and Sample Space S

All the elements of E are present in the superset S.

A sample space contains all of the possible outcomes or results of an experiment whereas an event is an outcome that actually occurred.

Random Experiment

A random experiment is defined as a procedure that produces a result that could not be predicted before the experiment.

It can be repeated many times but its outcomes are known in the sample space. An event is the result of a random experiment.

Probability

Probability is defined as how much there is a chance of an event occurring from a known set of outcomes. The probability is measured from 0 to 1.

The mathematical formula for probability is given as

P(E) = n(E) / n(S)

Where P(E) is the probability of an event to occur, n(E) is the number of favorable outcomes specified in an event E and n(S) is the total number of possible outcomes in the sample space S.

For example, a die is rolled. The probability of an even number occurring is demonstrated in figure 2.

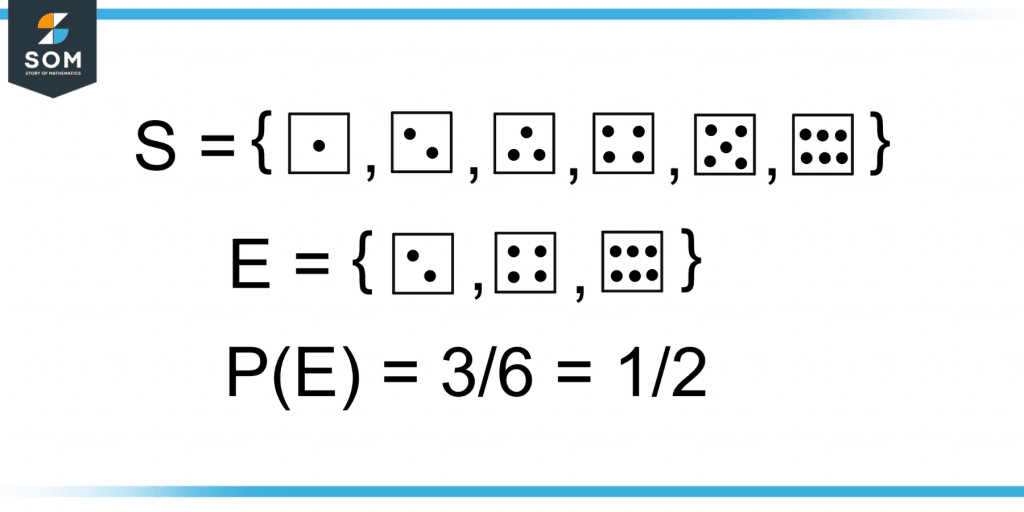
Figure 2 – Probability of an Even Number(Event) Occurring on a Die

Types of Events Based on Measure of Probability

Events can be classified on a basis of the values of probability. They are discussed below.

Impossible Event

As the name suggests, this type of event is impossible to occur in an experiment. This is because it is not included in the sample space of the experiment and has a probability of 0.

For example, an eight occurring on a die is an impossible event.

Unlikely Event

This type of event is unlikely to take place after an experiment. Its probability range is between 0 and 0.5 and its likelihood to occur increases as the probability increases.

For example, getting a two when a die is rolled is a very unlikely event as its probability is 0.16.

Equally Likely Events

These events have the same chance of occurrence, hence have equal probability values. They are also called evenly chanced events.

For example, a head or a tail occurring on a tossed coin is an equally likely event as both have the same probability i.e. 0.5.

Likely Event

An event is said to be likely when it has a probability greater than 0.5 but less than 1. For example, the chance of numbers 2, 3, 4, and 5 occurring on a die is a likely event as its probability is 0.67.

A likely event set has a maximum number of elements from its sample space but not all the elements.

Sure Event

A sure event is a certain event with a probability of one. It is sure to occur as it includes all the elements from the sample space.

For example, getting a red ball from a bag of red balls is a sure event.

Figure 3 shows the probability scale and the types of events.

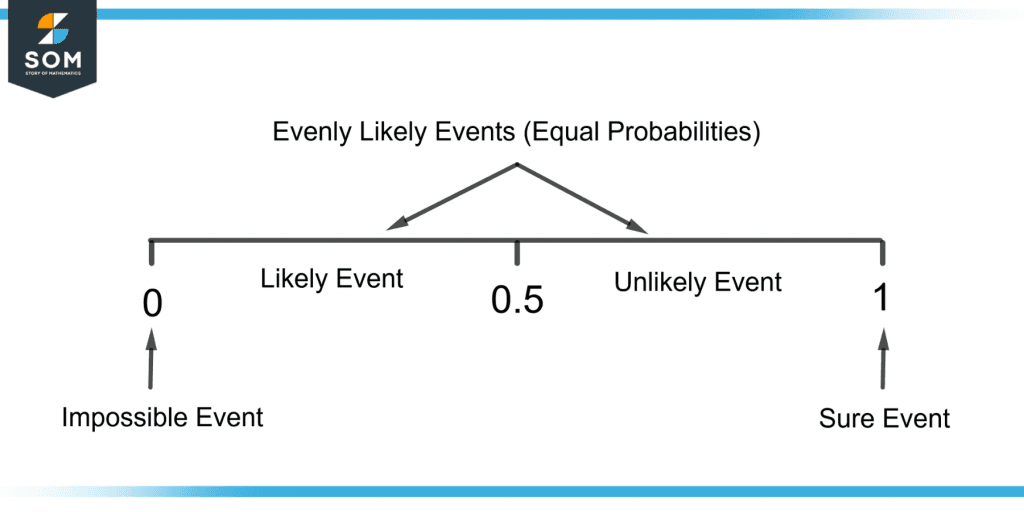
Figure 3 – Types of Events on the Probability Scale

Other Types of Events

Some other types of events are discussed below:

Simple and Compound Events

A simple event consists of one element of the sample space whereas a compound event contains more than one element. If

S = { 1, 3, 4, 7, 8, 11, 14 }

and

P = { 4 } , Q = { 1, 7, 11 }

Then P is a simple event and Q is a compound event.

Independent and Dependent Events

Two events not affecting each other are known as independent events. Contrarily, if the occurrence of an event is affected by the occurrence of the other event, then the two events are called dependent events.

Exhaustive Events

Events are called exhaustive when they occupy all the elements of the sample space. If

S = { 11, 12, 13, 14 }

Then

U = { 11, 13 } and V = { 12, 14 }

are exhaustive events.

Mutually Exclusive Events

Two events are said to be mutually exclusive if they cannot occur simultaneously.

If

S = { 6, 7, 8, 9, 10 }

Then

C = { 6, 7 } and D = { 9, 10 }

are mutually exclusive events.

Figure 4 shows the Venn diagram for the above two mutually exclusive events.

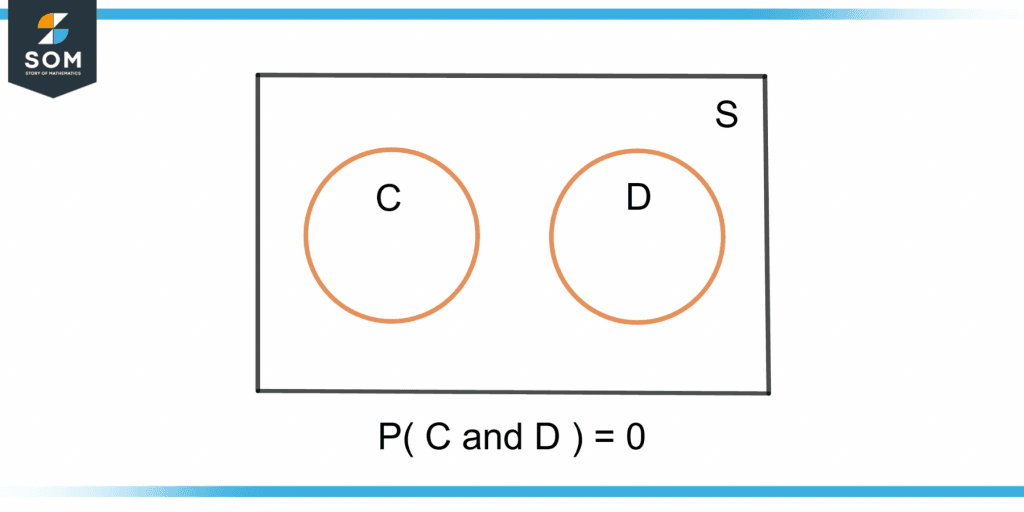
Figure 4 – Venn Diagram of Two Mutually Exclusive Events C and D

Both the events don’t have an intersection i.e. they don’t share an outcome.

Complementary Events

An event E has a complementary event E´ if E´ has all the elements of the sample space not in E. So,

E´ = S – E

Also,

P(E) + P(E´) = 1

E and E´ together make the sample space hence are exhaustive events. As both don’t have a common element, they are also mutually exclusive. If

S = { 25, 26, 27, 28, 29 }

and

F = { 26, 27 }

Then

F´ = { 25, 28, 29 }

is the complement of F.

“AND” Events

The AND operator denotes the intersection or common points between the events. AND is denoted by the intersection symbol “∩”. If

Q = { 1, 2, 3 }

And

R = { 3, 4, 5 }

Then

Q AND R = Q ∩ R = { 3 }

Figure 5 shows the two events Q, R, and their intersection Q ∩ R.

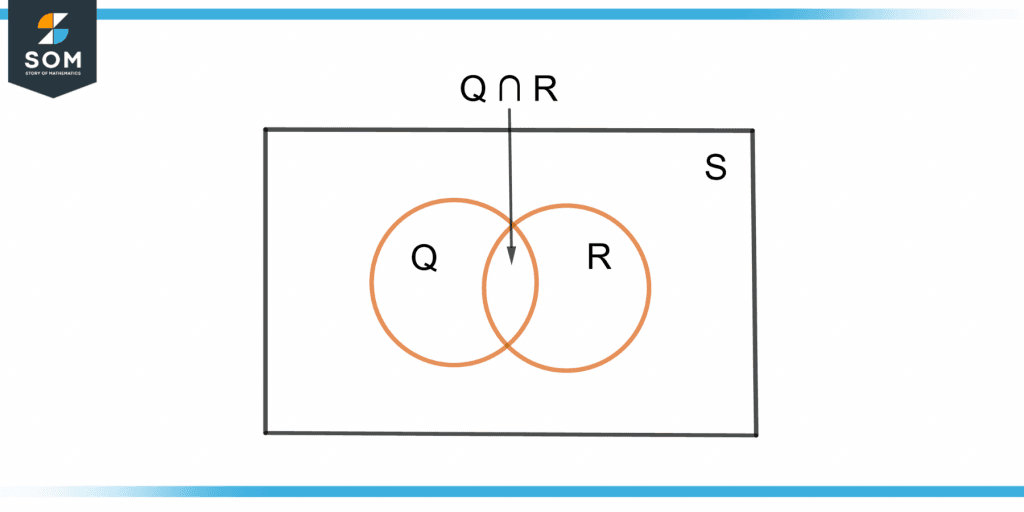
Figure 5 – Intersection of two events Q and R

“OR” Events

The OR is the union(∪) of elements of events. If

L = { 10, 20, 30 }

and

M = { 40, 50 }

Then

L OR M = L ∪ M = { 10, 20, 30, 40, 50 }

Figure 6 shows the Venn diagram for events L and M.

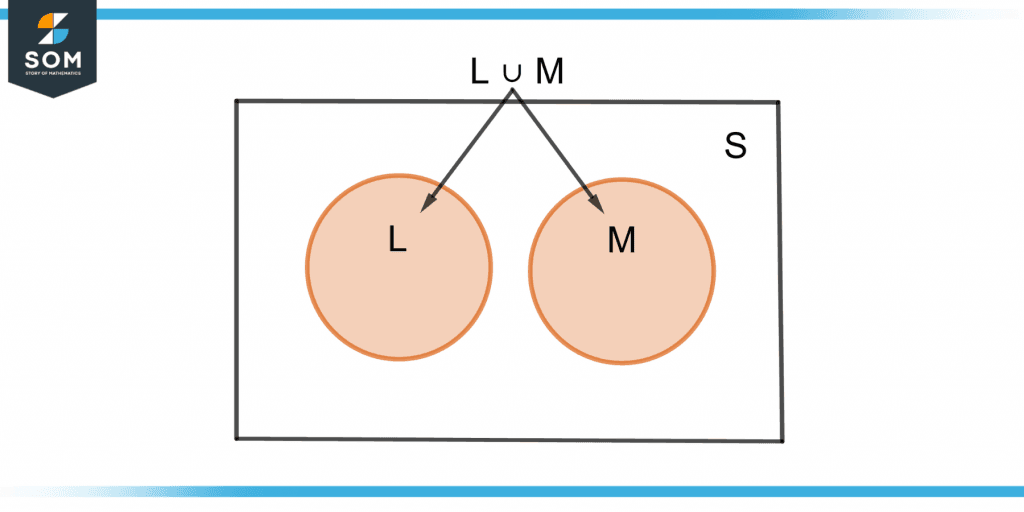
Figure 6 – Union of Two Events L and M

A Solved Problem of Event Classification

A deck of cards is shuffled. What is the probability that a heart card will occur when a card is picked? What type of event is it?

Solution

There are 52 cards in a deck and it has a total of 13 heart cards. So,

n(H) = 13

n(S) = 52

The probability of picking a heart card is

P(Q) = n(H) / n(S)

P(Q) = 13 / 52 = 0.25

So, event H is an unlikely event as its probability is between 0 and 0.5.

All the images are created using GeoGebra.

Even Number Definition < Glossary Index > Experiment Definition