Even Number|Definition & Meaning

What Are Even Numbers? 

An integer is said to be even if it can be precisely divided by 2 without leaving a remainder. The final digit of an even integer is always one of the following: 0, 2, 4, 6, or 8. Two, four, six, eight, ten, twelve, fourteen, and sixteen are all examples of even numbers. Because each of these numbers may be evenly partitioned by two, we call them even numbers.

It is essential to understand that the smallest natural Number that is both positive and even is 2. An odd number cannot be written as a fraction or expressed as a simple division by 2, for instance- 1, 3, 5, 7, 9, etc. Therefore, numbers can be separated into two categories: even and odd. That is to say, a number’s value can be either even or odd.

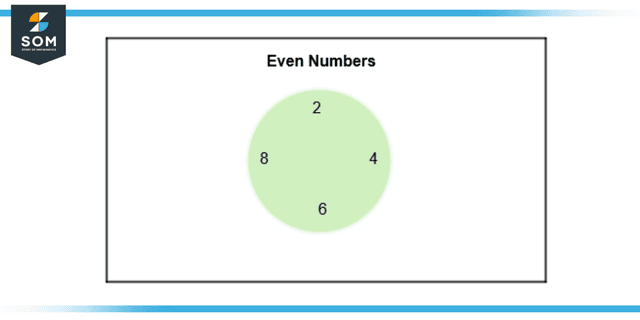
Figure 1: Representation of an even number in a sample space.

How To Differentiate Whether a Number is Even or Odd?

Checking the Number in the one’s place, also known as the unit’s place, is the way to determine whether or not the supplied Number is odd or even. If you use that exact Number instead of one, you will be able to determine whether or not the Number is odd or even.

Even numbers consist of the digits 0, 2, 4, 6, and 8.

Odd, The last digits of the numbers are 1, 3, 5, 7, and 9.

These straightforward methods can be used to determine whether or not the numbers are even.

Consider the numbers 3, 845, and 917, each of which terminates with an odd number, specifically 3, 5, and 7. Therefore, an odd number can be deduced from the supplied integers 3, 845, and 917. Because of this, the number does not constitute an even number. Similarly, 8, 322 is an even number because it concludes with 8 and 2.

Figure 2: Representation of even and odd numbers as mutually exclusive events

Even and odd numbers are mutually exclusive events because there are no such number in both of them.

Properties of Even Number

1. Adding two even numbers together will always produce another even number as the sum.
2. When an even number is subtracted from another even number, the result is also an even number.
3. When you multiply two even numbers together, you will always get back another even number.

Addition Property

• When even and odd numbers are added together (or vice versa), a sum is always an odd number.
  Ex: 10 + 5 = 15, 5 + 18 = 23
• When two even numbers are summable, the result is invariably another even number.
  Ex: 12+4 = 16
• When you add together two odd numbers, the sum you get is always an even number.
  Ex: 15 + 9 = 24

Subtraction Property

• When an even number is subtracted from an odd number (or vice versa), the number is always an odd number.
  Ex: 9 – 4 = 5, 12 – 5 = 7
• When an even number is subtracted from another even number, the resulting number is always an even number.
  Ex: 16 – 8 = 8
• When an odd number is subtracted from another odd number, the resulting number is always an even number.
  Ex: 21 – 11 = 10

Multiplication Property

• You will always get back an even number when you multiply two even numbers.
  Ex: 6 × 6 = 36, 12 × 2 = 24
• A result is an even number when you take the product of an even number by an odd number.
  Ex: 4 × 3 = 18, 6 × 5 = 30
• When you multiply two odd numbers, you will always get back an odd number.
  Ex: 7 × 5 = 35, 5 × 9 = 45 

The Function of Even Number

The congruence n=0 (mod 2) holds for even numbers because even numbers can be divided by two without leaving any remainder. It is said that an even number n is singly even if the equation n=2 (mod 4) also holds for it, and it is said that an even number n is doubly even if the equation n=0 (mod 4) holds for it.

The property of an integer that indicates whether or not it is odd is referred to as its parity; hence, an odd number has a parity of 1, whereas an even number has a parity of 0.

The function that is used to generate even numbers is:

$\mathsf{\dfrac{2x}{(x-1)^2}}$ = 2x + 4x$\mathsf{^2}$ + 6x$\mathsf{^3}$ + 8x$\mathsf{^4}$ + …

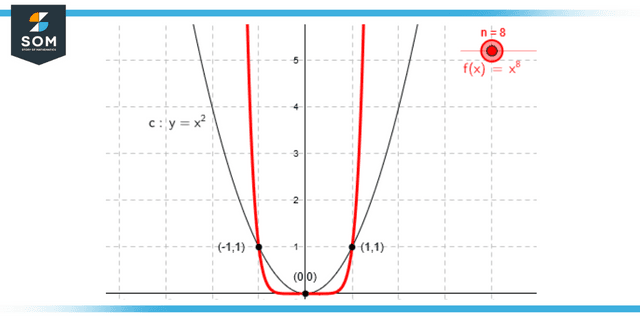
Figure 3: Representation of an even function by a graph.

When the power of function (x) is 2, the graph is represented with a black line and when the power of the function (x) is 8, the graph is represented with the red line.

Examples Involving Even Numbers

Example 1

Find the mean of the following even numbers:

12, 24, 8, 42, 2, 6, 38, 22, 34, 30, 48 and 40

Solution

Mean is finding the average of the given numbers. The mean of the above data can be calculated by adding all the even numbers and then dividing it by the total numbers of data provided in the set.

12 + 24 + 8 + 42 + 2 + 6 + 38 + 22 + 34 + 30 + 48 + 40 = 306

Now divide the answer 306 by 12 (the total number of values in the set.)

306 / 12 = 25.5

Example 2

Find the median of the following even numbers:

4, 62, 50, 20, 52, 8, 10, 44, 66, 34, 88, 92 and 2

Solution

Median is the middle number in the set. It is found by arranging the data from ascending (smallest) to descending (largest) order.

Now rearranging the set from ascending to descending order we get:

2, 4, 8,10, 20, 34, 44, 50, 52, 62, 66, 88 and 92

As the middle number here is 44. So, 44 is the median of the given set.

All images/graphs are created using GeoGebra.

Evaluate Definition < Glossary Index > Event Definition