Evaluate|Definition & Meaning

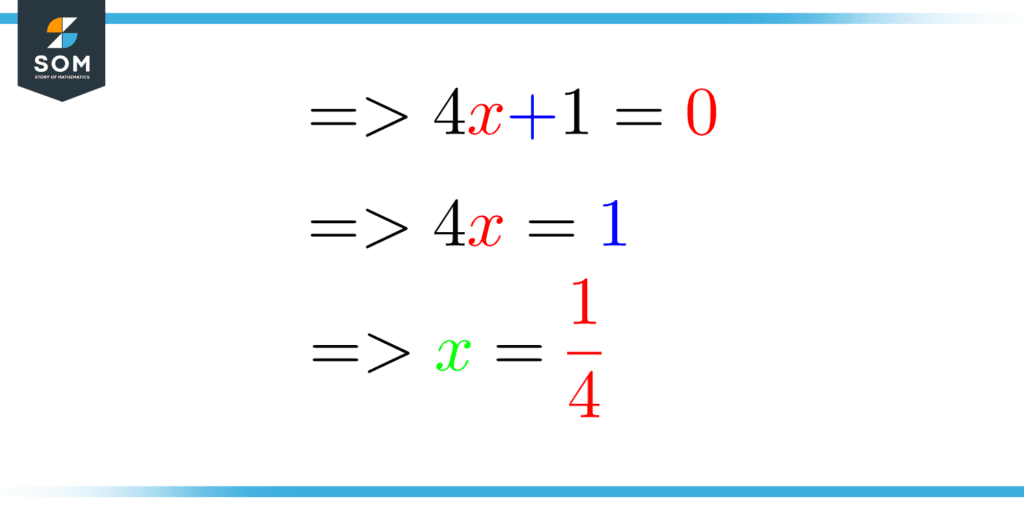
Figure 1: An algebraic expression that is evaluated to find the value of the variable “x” 

Expressions, such as simple mathematical operations between two numbers, always result in a numerical value that gives us the meaning of the expression in general. Thus, we can also say that finding the numerical value of an expression is mathematically said to evaluate the given expression.

Furthermore, expressions that include an algebraic variable also are evaluated to find the numerical value of the algebraic variable in the expression. This way, multiple problems are simplified into simple algebraic equations and expressions for ease of understanding and easy solving and evaluating of such problems.

Moreover, it is important to note that expressions or equations that are being evaluated must result in a constant numerical value. If the expression has a variable in it then this variable must be substituted by a constant value to evaluate the expression.

Simplify, Solve and Evaluate

In mathematics, explaining problems and what to find or calculate is usually done by using these three words or phrases: Evaluate, Solve, and Simplify. These words are most commonly used in exercises when finding solutions to various types of problems or just re-writing the expressions or problems in a way to easily understand the problem for which we need to find the solution.

As explained in the last section, evaluation is usually used to find a numerical value of an expression or an equation with no variables or equations as the result. The answer must always consist of a numerical value. An example of such type is to evaluate a given expression $2+2$ and by evaluating it, we obtain the answer four which is a numerical solution.

The word “solve” is usually used to explain the solution by isolating a particular variable in an equation such as those in quadratic equations. Here, we solve the quadratic equations for finding the value of x that satisfies the given equation. Furthermore, when using the word solve, it can either mean the solution is in the form of a variable or a constant value.

Moreover, solving an equation can also be done using graphical expressions to find the resulting curve equation or, for example, the roots of a curve given as a graph.

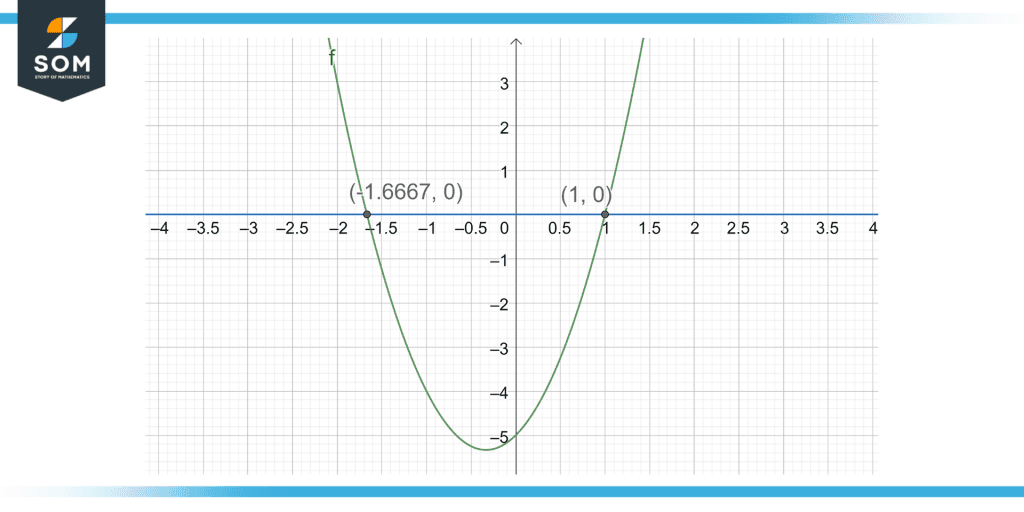
Figure 2: A curve of the equation $3x^2 + 2x – 5 = 0$ shown with its roots at the intersection point to the x-axis.

Finally, simplify is used to rewrite complicated equations or expressions into easier alternate versions of the expressions that will help in finding the solution to the problem more easily. This simplification can be explained by simplifying quadratic equations using different techniques to rewrite them into simpler multiple forms.

Examples Featuring Evaluations of Expressions and Equations

Example 1

An equation is given below:

y = 5x$^2$ + 3x – 3

Simplify this expression and evaluate this when the expression is equal to zero

Solution

To simplify this expression, we utilize the completing square method to rewrite the equation into an easier expression.

 y = 5x$^2$ + 3x – 3

y = 5$\left(x^2+\dfrac{3}{5}x-\dfrac{3}{5}\right)$

y = $5\left(x^2+\dfrac{3}{5}x-\dfrac{3}{5}+\left(\dfrac{3}{10}\right)^2-\left(\dfrac{3}{10}\right)^2\right)$

y = $5\left(\left(x+\dfrac{3}{10}\right)^2-\dfrac{3}{5}-\left(\dfrac{3}{10}\right)^2\right)$

y = $5\left(\left(x+\dfrac{3}{10}\right)^2-\dfrac{69}{100}\right)$

 y = $5\left(x+\dfrac{3}{10}\right)^2-\dfrac{69}{20}$

Thus we rewrite this expression into a simpler form.

Now we will evaluate this expression with the value of y equal to zero.

$5\left(x + \dfrac{3}{10}\right)^2-\dfrac{69}{20} = 0$

$5\left(x + \dfrac{3}{10}\right)^2 = \dfrac{69}{20}$

$ \left(x + \dfrac{3}{10}\right)^2 = \dfrac{69}{100}$

$x + \dfrac{3}{10} = \sqrt{\dfrac{69}{100}} $

x = $- \dfrac{3}{10} \pm \dfrac{\sqrt{69}}{10}$

Thus the above value of x is evaluated to be either 0.531 or -1.131.

Example 2

A quadratic equation is given such that:

 x$^2$ + 2x – 3 = 0

Evaluate the roots of the variable x in this equation by first simplifying the equation into a simpler form. Also, draw a graph to further confirm that the roots are verified.

Solution

For this example, we are given a quadratic equation that can be easily simplified into an alternate expression by using the completing square method. This way, the solution can be easily found with fewer steps at the end.

x$^2$ + 2x – 3 = 0

 x$^2$ + 2x + 1$^2$ – 3 – 1$^2$ = 0

(x + 1)$^2$ – 3 – 1 = 0

(x + 1)$^2$ – 4 = 0

(x + 1)$^2$ = 4

x + 1 = $\pm\sqrt{4}$

x + 1 =$ \pm$ 2

x  = – 1 $\pm$ 2

Thus the above value of x is evaluated to be either -3 or 1.

Furthermore, the above value can be verified by drawing the graph of the quadratic equation and finding the intersecting points on the x-axis that are the roots of the x.

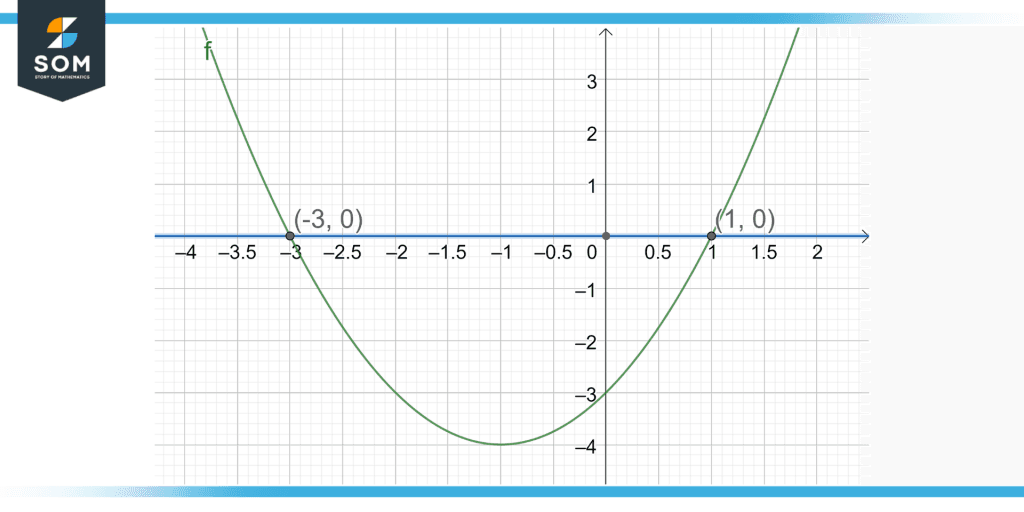
Figure 3: A graph showing the roots of the quadratic curve thus verifying the calculation done in the example.

Example 3

An algebraic equation is given below:

4x + 3x + 9 = 33

Evaluate the above algebraic equation to find the value of x

Solution

This is a fairly simple equation to evaluate and the following is the process to evaluate the value of x.

 4x + 3x + 9 = 33

7x  = 33 – 9

7x  = 24

x  = $\dfrac{24}{7}$

Hence, the equation is evaluated to find the value of x being 24/7 or 3.42

All drawings and mathematical graphs are made using GeoGebra.

Estimate Definition < Glossary Index > Even Number Definition