Estimate|Definition & Meaning

Figure 1 shows some small triangles in a box and the estimated result of the number of triangles in the box without counting. 

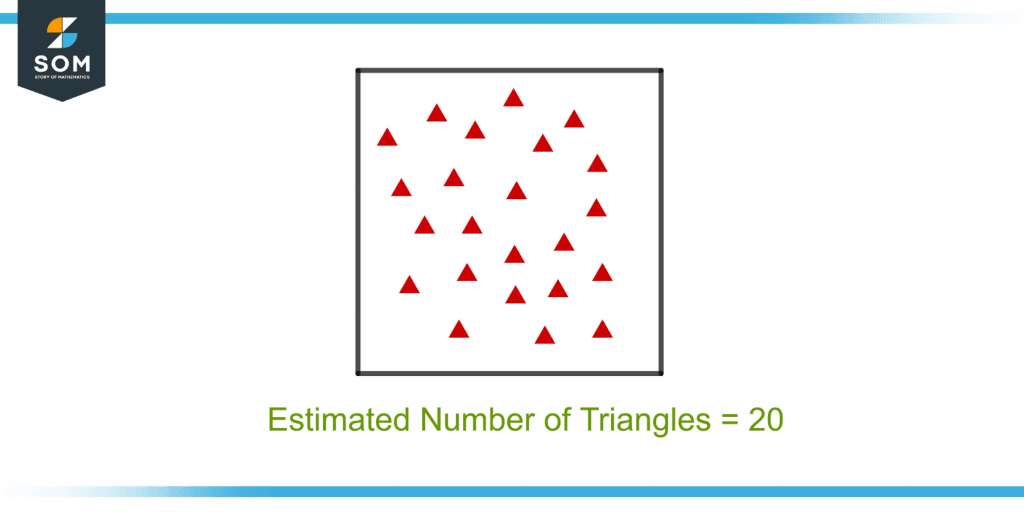
Figure 1 – Demonstration of the Estimated Number of Triangles in a Box

Estimation in Real-life Calculations

Estimation is performed so often in real life as it helps to form an idea about a certain thing in a very few seconds without doing calculations. For example, we can estimate the total number of books present on the shelf in a library.

The estimated result, if the person is good at estimation, is often close or near to the actual result. The difference is that the estimated result is calculated when there is a time constraint, and the time to calculate the actual result is insufficient.

For example, if you want to buy 6 books from the bookshop, that costs $2.95 each. The seller says the total price of 6 books equals $20. Now, you can check the total price by quickly estimating the result in your mind as:

2.95 dollars is almost equal to 3 dollars

So, when $3 is multiplied by 6 books, the total price comes out to be $18. The seller was telling you $20, which is obviously more than the actual price, as the estimated $18 price comes from approximately increasing the price, i.e., to 3 dollars instead of $2.95. Hence, you tell the seller to recheck the total selling price.

Here, the power of estimation saves you with the help of approximating some numbers in the calculations, i.e., in the above case, the price of one book.

Approximation

An approximation is defined as something that is similar but not exactly equal to the actual value, description, quantity, image, etc. It is abbreviated as “approx.” and usually applies to numbers. For example, if the time is 8:55 a.m., it can be approximated to 9:00 a.m. as it is close to the actual time.

The approximation is similar to estimation, but it is used in scientific terminology, whereas estimation can be used in any real-life problem.

The approximation is used if the required data is not completely available, the problem’s sensitivity to this data, the time constraint, and how much accuracy is required is the solution.

Approximations are also made in scientific experiments. This is because some factors from the real situation are left out to simplify the calculations. For example, the frictional force is not included when calculating the force applied on an object which makes the result an approximation.

Different Symbols for Approximation

It is denoted by “,≈” which is read as “almost equal to.” This symbol is usually used to indicate approximation between numbers such as e ≈ 2.718. The symbol “≌” means “approximately equal to” and approximates the congruence in figures, e.g., triangle LMN ≌ triangle ABC. The symbol “≉” denotes “not almost equal to,” e.g., 3 ≉ 5 but 3 ≈ 3.2.

Equality

Equality is defined as the relationship between two or more quantities or mathematical expressions, saying that the two expressions or objects represent the same value. The symbol of equality is “=,” and C = D is read as “C is equal to D.”

In estimation, equality has an important role as the estimated value should be close to the actual value. If the actual value is not known, an estimation of the value can be found. 

Exact and Estimated Value

The exact and estimated value comes from the concept of equality and approximation. The estimated value approximates the exact value, i.e., it is close to the actual value. For example, the estimated value of the length of a line, equal to 12.7 cm(exact value), is 13 cm.

Advantages of Estimation

The following are some advantages of estimation.

Time-Saving

Estimated results are always calculated when the time required for the answer is very short. It saves a lot of time while also checking the accuracy of results to a point. For example, roses that are 7 cm apart need to be planted in a 68.6 cm long row. Here the calculation does not need to be exact, so estimation can save time as:

68.6 cm is almost 70 cm

70 cm divided by 7 is 10

So, 10 roses 7cm apart should be enough to plant in a 68.6 cm long row.

Detection of Mistakes in Calculations

Estimation can detect mistakes in calculations as human error is possible. It comes in handy when the results need to be cross-checked. For example, to calculate 105 times 65, the calculator shows 975. To cross-check, approximating 105 to 100 and 65 to 60, the estimated answer is:

100 ✕ 60 = 6000

But why the calculator shows 975 as the product of 105 and 65? It is not even close to the estimated value, i.e., 6000. It means some mistake occurred while typing the numbers in the calculator. The person typed 15 instead of 105, whose product is 975, which led to an error. Hence, it is really important to cross-check your results by using estimation.

Also, estimation is performed as a calculator is not always available to do difficult calculations.

Improves Mental Math

Estimation helps to improve the skill of doing math with your mind and not to use any calculator. The more practice of estimation is performed in real life, the more the person becomes an expert in it.

Different Strategies of Estimation

An estimated result can be calculated using different strategies.

For example, to add 398 and 650, one way is to approximate the number 398 to 400 and then add it to 650, i.e.,

400 + 650 = 1050.

The other way is to add up to the tens place of both the number, i.e., 98 and 50 of the numbers 398 and 650, respectively, as:

98 + 50 = 148

The number 148 is nearly equal to 150, hence adding the hundreds of both the numbers, i.e., 300 and 600 with 150, gives the estimated result as:

300 + 600 + 150 = 1050

A person develops his/her own strategies to find the estimate of a problem, as different problems require different strategies.

Visual Estimation

Visual estimation is the process of estimating how big or small, how long or wide, and how many things are present by using the visual sense. This includes the estimation of counts and lengths, as discussed below.

Estimation of Counts

The estimation of counts requires finding the approximate number of the objects present without counting them. For example, many diamonds are shown in figure 2.

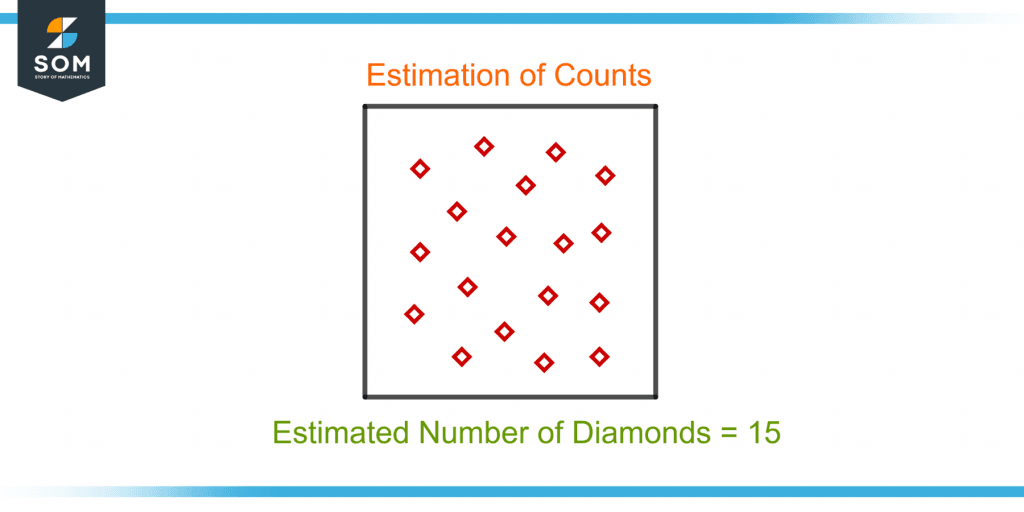
Figure 2 – Demonstration of Estimation of Counts

A person can estimate the total number of diamonds just by looking at them without counting them. The estimated value will be close to 18(exact); e.g., 15 is an estimated value.

Estimation of Lengths

The estimation of lengths involves estimating the measurements of lengths that are close to the exact measurement. For example, two squares are shown in figure 3. The length of the small square is 1 m. What is the estimated length of the big square?

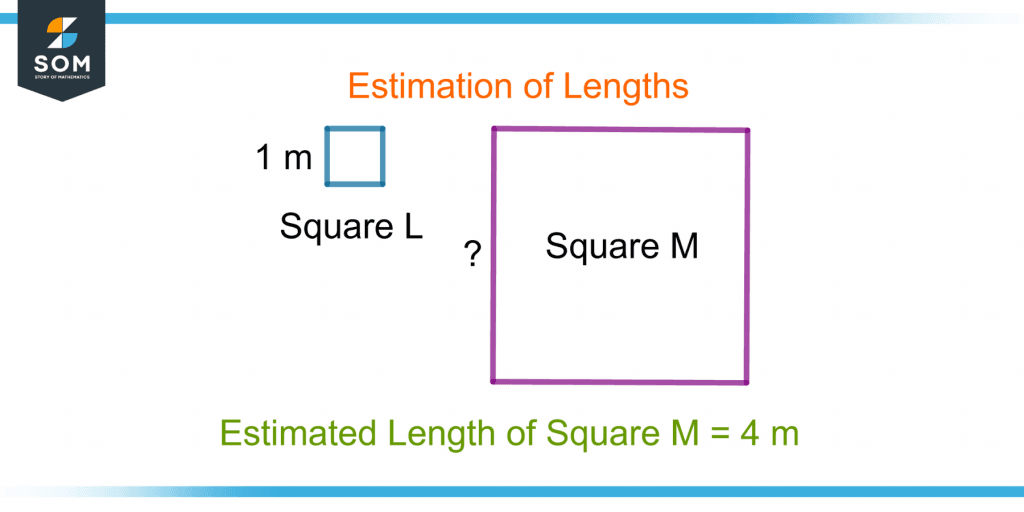
Figure 3 – Demonstration of Estimation of Length

The estimated length of the square can be 4 m, but the exact length is 4.5 m.

An Example Involving Estimation

Two rectangles, A and B, are shown in figure 4.

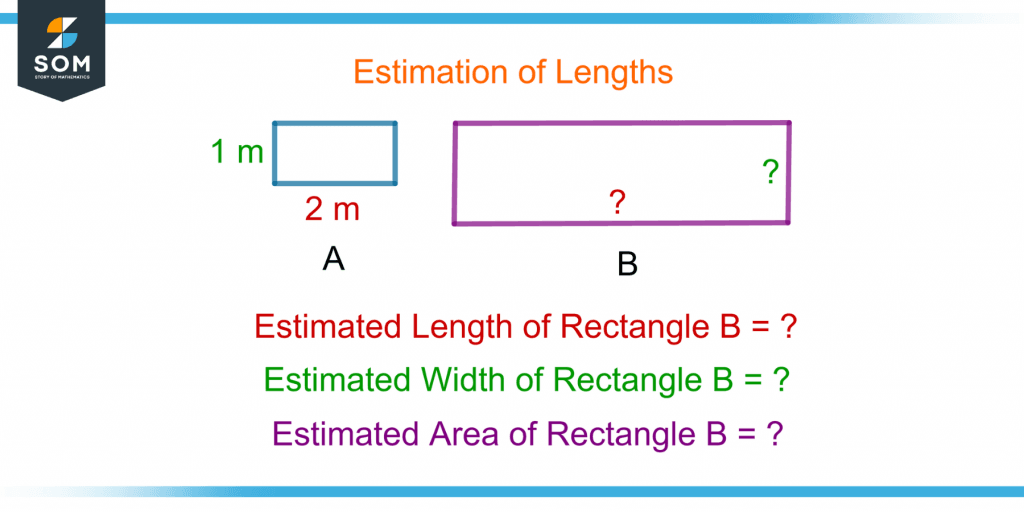
Figure 4 – Example of Estimating the Length and Width of a Rectangle and Finding the Estimated Area

If the length of the small rectangle is 2 cm and its width is 1 cm, estimate the length and width of the big rectangle and find its estimated area.

Solution

The estimated length of the big rectangle is 6 cm as the length of the big rectangle seems three times the length of the small rectangle, i.e., 2 cm as:

Estimated Length of Rectangle B = 2 ✕ 3 = 6 cm

Its estimated width is 2 cm as the big rectangle’s width seems two times the width of the small rectangle, i.e., 1 cm.

Estimated Width of Rectangle B = 1 ✕ 2 = 2 cm

The area of a rectangle is given by the formula:

Area = Length ✕ Width

Placing the values of estimated length and width to get the estimated area as:

Estimated Area of Rectangle B = 6 ✕ 2 = 12 cm$^2$

All the images are created using GeoGebra.

Equilateral Definition < Glossary Index > Evaluate Definition