Equilateral|Definition & Meaning

It is possible to calculate the area, perimeter, and height of an equilateral triangle in the same way that these measurements can be calculated for other triangles. 

What Is a Triangle With Equilateral Sides?

Additionally, all three of the triangle’s angles add up to a total of sixty degrees and are congruent. The total angle equals 180 degrees when all three angles are added together in a triangle with equilateral sides. 60° + 60° + 60° = 180°. As a result, it satisfies the requirements of the angle sum attribute of triangles.

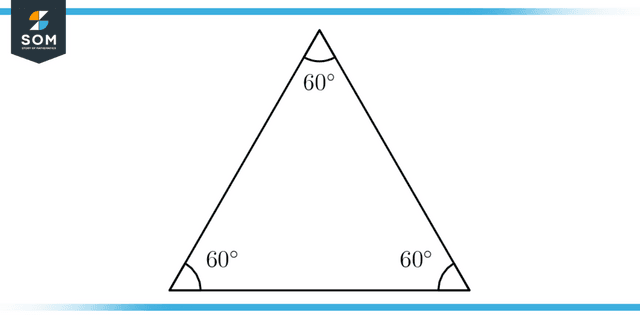
Figure 1: Representation of Equilateral Triangle

The Shape of an Equilateral Triangle

An equilateral triangle displays the outline of a regular shape. It is sometimes termed a regular polygon or regular triangle since all its sides are equal.

Let us suppose that the triangle ABC is equilateral by definition;

The formula for the equilateral triangle is as follows: AB = BC = AC, where AB, BC, and AC are the sides of the triangle.

And

∠A = ∠B = ∠C = 60°

There are also two other kinds of triangles, distinguished by the sides they have:

• Scalene Triangle
• Isosceles Triangle

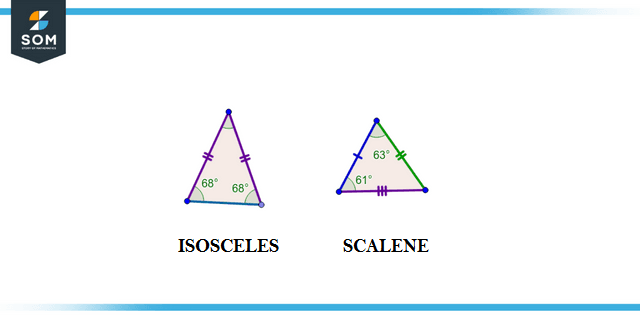
Figure 2: Scalene and Isosceles Triangle

Characteristics of Equilateral Triangles

Equilateral Triangles Have the Following Characteristics:

1. Every one of the three sides is equivalent.
2. The sum of the three angles, which add up to sixty degrees, makes them congruent.
3. The polygon has three straight sides, making it a regular shape.
4. The equilateral triangle is divided into two halves by the perpendicular. In addition, the angle of the vertex, measured from the point where the perpendicular is drawn, is cut in half to create two equal angles, each of which is equal to 30 degrees.
5. The same point serves as both the orthocenter and the centroid of the figure.
6. When describing an equilateral triangle, it is essential to note that each side’s median, angle bisector, and altitude values are identical.
7. The area of an equilateral triangle can be computed with the formula: [($\sqrt{3}$/4).b²].
8. A triangle with equilateral sides has a perimeter equal to 3b.

Equilateral Triangle Theorem

If triangle XYZ is an equilateral triangle, and point P is located on the circumcircle of triangle XYZ, then the following statements are factual:

PX = PY + PZ

As evidence, consider the following for a circular quadrilateral XYPZ:

PX.YZ = (PY.XZ) + (PZ.XY)

Given that we are aware, in the case of an equilateral triangle XYZ:

XY = YZ = ZX

Therefore:

PX.AY = (PY.XY) + (PZ.XY)

Using XY as a common denominator:

PX.AY = XY(PY+PZ)

PX = PY + PZ

Therefore, it is proven.

Area of a Triangle With Equilateral Sides

The region of a two-dimensional plane occupied by an equilateral triangle is referred to as the triangle’s area. The following equation is used to calculate the area of an equilateral triangle:

A = [($\sqrt{3}$/4).a²]

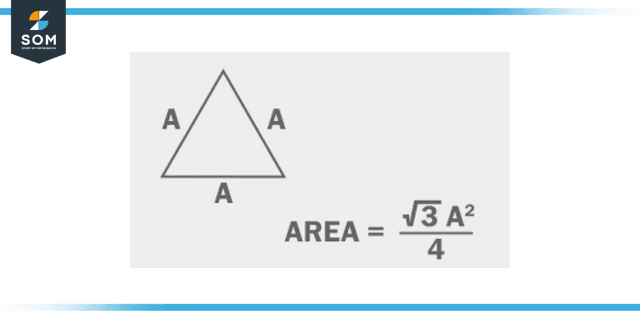
Figure 3: Area of Equilateral Triangle

The Perimeter of a Triangle With Equal Sides

In geometry, the length of the sides of a polygon is used to calculate its perimeter. The perimeter of an equilateral triangle is equal to the total of its three sides. Hence this value is used to describe the shape.

Let’s say that XYZ is an equilateral triangle. In that case, the perimeter of ABC is as follows:

Perimeter = XY + YZ + ZX

P = b + b + b

P = 3b

In this equation, b represents the length of one of the triangle’s sides.

Measurement of the Axis of an Equilateral Triangle

The height of an equilateral triangle, having similar sides, can be computed using the Pythagorean theorem, given its base and height. In some contexts, it may also be referred to as the altitude of an equilateral triangle. Now, if we take an elevation from the triangle’s apex and drop it down to the base, we may divide it into two right triangles that are equal in size.

As a result, we can get the height (h) of the equilateral triangle using the diagram that was just presented by using the formula:

h = $\sqrt{3}b/2$

Where b represents one of the triangle’s sides.

The Apex of a Right Triangle

At its geometric center, an equilateral triangle’s centroid can be found. Since all sides are the same length, determining its centroid is a breeze.

The centroid can be located by connecting the opposite sides of the triangle with perpendiculars drawn from the three vertices. These perpendiculars all meet at the same point, the centroid, and are the same length.

Circumcenter

The circumcenter of an equilateral triangle is the position of union perpendicular bisectors of the sides. This triangle has a circumcircle that touches all three of its corners.

In geometry, a triangle is equilateral if its in-center, orthocenter, or centroid lies on the same line as its circumcenter.

Example 1

Find the base of the triangle, having two similar sides. Given that an equilateral triangle has a side of 16 cm, which has a perimeter similar to an isosceles triangle, having a side of 23 cm.

Solution

Since the perimeter is the same for both triangles, it can be written as follows:

Perimeter of Equilateral = Perimeter of Isosceles Triangle

3 x 16 = (2 x 23) + Z

48 = 46 + Z

Z = 2 cm

Here, the side of the equilateral triangle is multiplied by three since all sides are equal, whereas isosceles has two sides equal; therefore, multiplied by two. And the variable Z is left as the base.

Example 2

An equilateral triangle has a perimeter of 8 cm; find the height of the triangle.

Solution

a = (8 / 3) = 2.67

h² = [a² – (a² / 4)]

h = $(\sqrt{3} / 6)$ x 8

h = 2.3 cm

The height of the triangle is 2.3 cm.

All mathematical drawings and images were created with GeoGebra.

Equidistant Definition < Glossary Index > Estimate Definition