Exponent|Definition & Meaning

We sometimes read numbers in words such as hundred, thousands, up to crores, and so on. What happens if a number has more digits than we can read? For example,  5972190000000000000000000 kg is the mass of Earth. This number cannot be read in simple words. Thus, making it easy to pronounce these types of numbers, we put the exponents to work. 

Figure 1 – Exponent of a Number

Exponentiation is a mathematical process, written as bⁿ, which includes two numbers, the base b and the exponent or power n, and pronounced as “b (raised) to (the power of) n“.  When n is a positive integer. In the above figure, b is 6, and n is 2. Exponentiation corresponds to repeated multiplication of the base b, and bⁿ is the product of multiplying base n times:

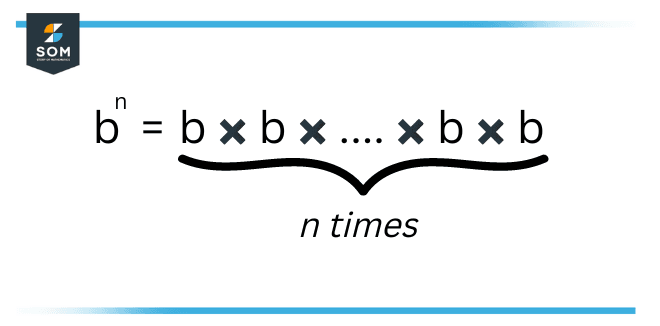
Figure 2 – Exponent is Multiplied n times with the Base

For example, 5 is multiplied by itself 3 times, that makes, 5 x 5 x 5. This can also be written as 5^3. Here, 5 is the base, and 3 is the exponent. This can also be read as 5 is raised to power 3.

Exponent Symbol

The symbolic representation for the exponent is ^. The name of this symbol (^) is a carrot. For example, 8 raised to the times 2 can be written as 8². Thus, 8² = 8 x 8 = 64. The table below shows the model of a few numerical expressions using exponents.

Figure 3 – Table Representing Exponent Values

Exponent Laws

Other laws of exponents are mentioned below, which are based on the powers they bear.

Multiplication Law: Apply on bases multiplying the same ones, add the exponents or powers and the base should be kept the same. When bases are raised with power to another, keep the base the same and multiply the exponents.

Division Law: Apply on bases dividing the same ones; subtract the power of the denominator from the power of the numerator while keeping the base the same.

Let’s say  ‘p’ is any integer or a decimal number and ‘a’, and ‘b’ are positive integers, that means the powers to the bases such that the above laws can be written as:

• p^a. p^b = p^a+b
• (p^a)^b = p^ab
• (pq)^b = p^b q^b
• (p/q)^b = p^b/q^b
• p^a/p^b = p^a-b
• p^a/p^b = 1/p^b-a

These laws show us the above properties of exponents. These laws are used to write large numbers in an understandable manner and to simplify complex algebraic expressions.

Exponent and Powers

As described above, the exponent is the number of times a number is multiplied by itself. The power is an expression that tells us about the repeated multiplication of the same number. For example, in the expression 5³, 3 is the exponent, and 5³ is called the 5 to the power of 3. This means, 5 is multiplied by itself 3 times.

Negative Exponents

A negative exponent is handled differently in exponents. In the Negative exponent, the multiplication of reciprocals of bases takes place. The multiplication of reciprocals is done n times (exponent value). For instance, if it is provided that a^-n, it can be written in its reciprocal form as 1/aⁿ. It indicates we have to multiply 1/a ‘n’ times.

Negative exponents are utilized when noting fractions with exponents. Few samples of negative exponents are 2 x 3^-9, 7^-3, 67^-5, etc. We can transform these fractions into positive exponents as:

• 2 × 3^-9 = 2 × (1/3)⁹ = 2 / 3⁹
• 7^-3 = 1 / 7³
• 67^-5 = 1 / 67⁵

Exponents With Fractions

• 5^2/3= (5²)^1/3 = 25^1/3 =  $\mathsf{\sqrt[3]{25}}$
•  -8^1/3 = ((-2)³)^1/3 = -2
• 10^5/6 = (10⁵)⁶ = $\mathsf{\sqrt[6]{10^5}}$ = $\mathsf{\sqrt[6]{100000}}$

Decimal Exponent

A decimal exponent is an exponent in which the power of a number is decimal. It is a little challenging to calculate the right answer to decimal exponents, so we find the approximate solution in such scenarios. Decimal exponents are evaluated by first shaping the exponent from decimal to fraction form. For instance, 4^1.5 can correspond to 4^3/2, which can be again simplified to obtain the last answer, 8. That is, 4^3/2 = (2²)^3/2 = 2³ = 8.

Scientific Notation With Exponents

For noting very big numbers or very small numbers, scientific notation is used as the Standard form. In the standard form, the numbers are noted with the assistance of 10’s powers and base decimals. A number is denoted in scientific notation if it is between  0 to 10 and multiplied by an exponent of 10. The exponent of 10 will be positive if the numeral is greater than 1, while the power of 10 will be negative if the number is less than 1. The below steps will explain how to write numbers in scientific notation using exponents.

• Step 1: After the first integer of the numeral from the left, place a decimal point. we don’t require to place a decimal in a number if there is only one integer in a numeral except for zeros.
• Step 2: Take the product of that number with an exponent of 10 so that the exponent number becomes equal to the times we move the decimal point in the base.

By observing these two easy steps, we can transform any numeral in standard utilizing exponents, for instance, 560000 = 5.6 x 10⁵, and 0.00736567 = 7.36567 x 10^-3.

A Solved Example Involving Exponents

Simplify the below expression:

(3² x 3^-5) / 9^-2

Solution

In the first step, shift 9^-2 to the numerator by taking the negative of the exponent.

= (3² x 3^-5) x 9²

In second step add 3^2-5 and re-write 9 as 3²:

= 3^-3 x (3²)²

Multiply the exponents 2 x 2 = 4:

= 3^-2 x 3⁴

In the third step, add the exponents as the bases are the same.

= 3^-2+3

= 3²

= 9

All images/mathematical drawings were created with GeoGebra.

Experiment Definition < Glossary Index > Exponential Function Definition