JUMP TO TOPIC
Exponential Function|Definition & Meaning
Definition
An exponential function is a function of the form $\mathsf{f(x) = a^x}$, where “a” is a constant value and “x” is a variable. “a” is called the function’s base and should be bigger than 0.
Function of Exponential
An exponential function is a form of a mathematical function that can be used to determine the growth or decay of a population, money, or price that grows or decays exponentially.
Jonathan was reading a news piece about the most recent bacterial growth study. He read about an experiment with a single microbe. After an hour, the bacterium had doubled in size and was two in number. The number was four after the second hour. Every hour, the number of germs increased. He was wondering how many bacteria would be left after 100 hours if this pattern continued. When he asked his teacher about it, he was given the concept of an exponential function as a response.
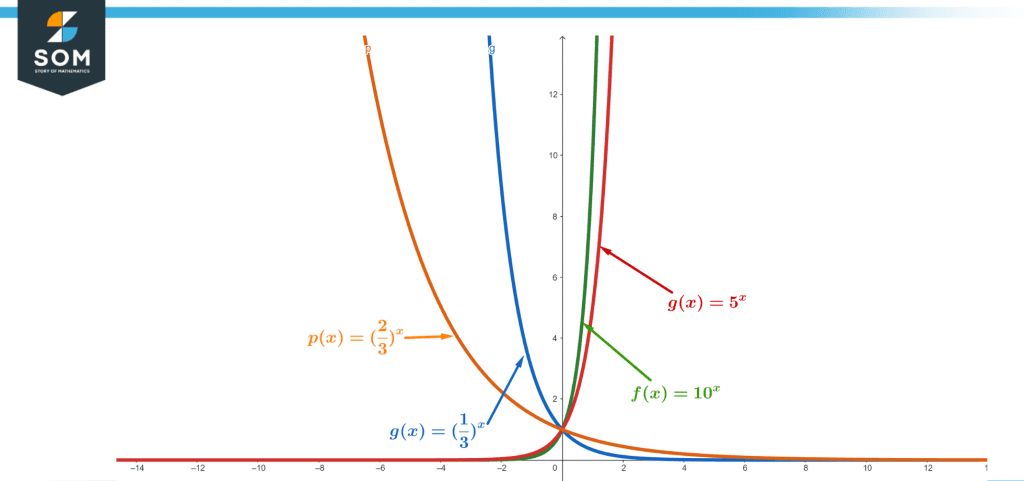
Figure 1 – Graph of multiple Exponential Functions
What Exactly Is the Exponential Function?
Exponents are used in the exponential function, as the name implies. However, an exponential function has a variable as its exponent and a constant as its base but not vice versa (A power function is one that has a variable as its base and a constant as its exponent but is not an exponential function).
Examples of Exponential Functions
Here are some exponential function examples.
\[ f(x)=4^x \]
\[ f(x) = (2/3)^x \]
\[ f(x) = 13e^{(12x)} \]
\[ f(x) = 15 (11)^{-0.25x} \]
The Formula for the Exponential Function
A basic exponential function is defined as f(x) = mx, where ‘m’ is a constant value and ‘x’ is a variable. $ f(x) = e^x $ is a popular exponential function, where ‘e’ is “Euler’s number” and e = 2.718… Extending the possibilities of many exponential functions, an exponential function may include a constant that is a power multiple of the variable. In other words, an exponential function can also take the form $ f(x) = qe^{kx} $. It can also have the form $f(x) = e^{kx}$, where q is a constant.
As a result, an exponential function can take one of the following forms.
\[ f(x) = b^x \]
\[ f(x) = ab^x \]
\[ f(x) = abc^x \]
\[ f(x) = ek^x \]
\[ f(x) = e^x \]
\[ f(x) = pe^{kx} \]
\[ f(x) = e^{kx} \]
All letters except ‘x’ are constant values, f(x) is an exponential function in terms of x, and x is a variable. Also, each exponential function’s base must be a positive number. In the preceding functions b > 0 and e > 0 Furthermore, b shouldn’t be equal to 1 (if b = 1, the function $$ f(x) = b^x $$ becomes f(x) = 1, and the function is linear but NOT exponential in this case).
- When the value of a quantity increases in exponential growth and drops in an exponential decay, the exponential function appears.
- In exponential growth, a quantity gradually increases at first, then rapidly increases.
- The exponential growth formulas are used to simulate population expansion, compound interest, and doubling time, among other things. The function’s graph in exponential growth is rising.
- In the case of exponential decay, a quantity drops rapidly at first, then slowly. The exponential decay is useful for modeling population decay, determining half-life, and so on. The function’s graph in exponential growth is dropping.
Graph of an Exponential Function
Using several examples, we may better comprehend the process of charting exponential functions. Let’s draw two graphs: $$ f(x) = 3^x $$ and $$ g(x) = (2/3)^x $$.
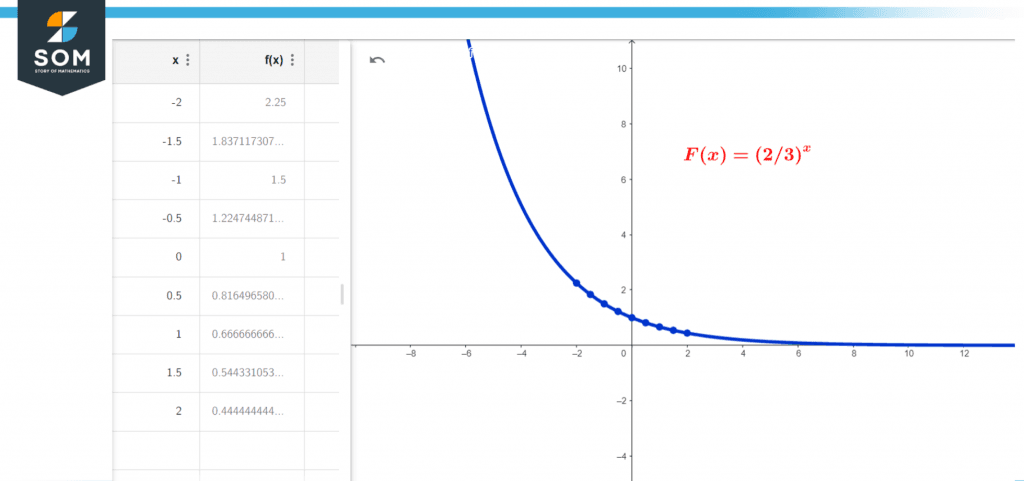
Figure 2 – Exponential decaying function table and graph
To graph each of these functions, we should make a value table with some random x values, plot the points on the graph, connect them with a curve, and extend the curve on both ends.
The exponential function $ f(x) = 3^x $ graph and table values are shown below.
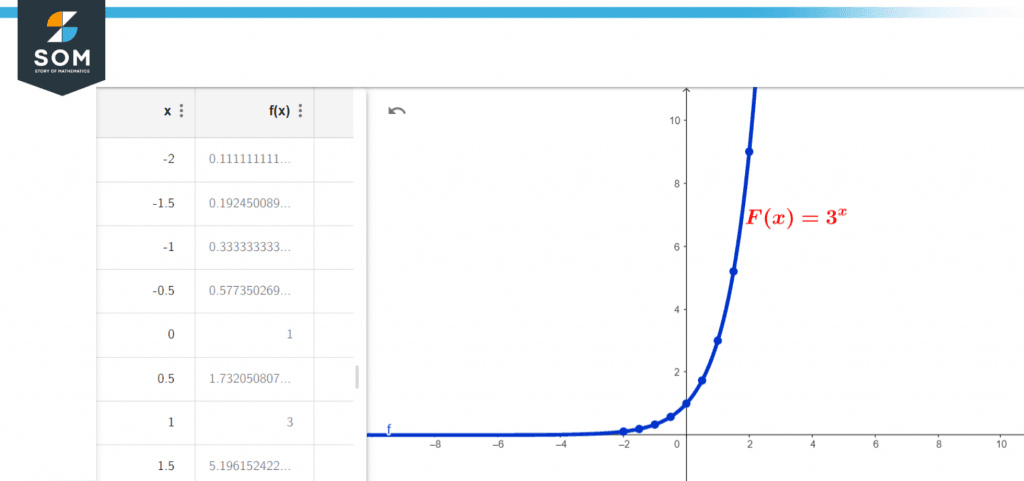
Figure 3 – Exponential increasing function table and graph
Asymptotes of Exponential Functions
Because the exponential function is continuously increasing/decreasing, there is no vertical asymptote. However, it possesses a horizontal asymptote. The horizontal asymptote equation of an exponential function, $$ f(x) = ab^x + c $$, is always y = c. That is, “y = constant being added to the exponent part of the function.” The horizontal asymptote in both graphs of ( $ f(x) = 3^x $ and $ g(x) = (2/3)^x $ ) is y = 0 ) because nothing is added to the exponent component in both functions. Thus,
A vertical asymptote is never found in an exponential function.
y = c is the horizontal asymptote of an exponential function $$ f(x) = ab^x + c $$.
Exponential Function Domain and Range
We are aware that the set of all x-values (inputs) for which a function can be computed is known as the domain of function y = f(x), and the set of all y-values (outputs) for which the function can be computed is known as the range. We can see from the graphs of $$ f(x) = 3^x $$ and $$ g(x) = (2/3)^x $$ in the preceding section that an exponential function may be constructed for any x value. Thus, an exponential function’s domain is the set of all real numbers (or) (-∞, ∞). The graph’s horizontal asymptote, let’s assume y = d, and whether the graph is above or below y = d, can be used to calculate the range of an exponential function. As a result, with the exponential function: $$ f(x) = ab^x $$
The domain is the collection of all real numbers or ($\-infty$, $+\infty$).
If a > 0, the range is f(x) > d, otherwise a < 0 for f(x) < d.
A Solved Example of an Exponential Function
Simplify the following exponential expression: \[ 4^{3x} +4^{3x+2} \]
Solution
Given exponential equation: \[ 4^{3x} +4^{3x+2} \]
By using the property: $$ m^x m^y = m^x+y $$
Hence: $$ 4^{3x+2} $$ Which can be written as: $$ 4^{3x} 4^2 $$
Thus the given equation is written as:
\[ 4^{3x} +4^{3x+2} = 4^{3x} + 4^{3x} 4^2 \]
Now, factor out the term: $$ 4^{3x} $$
\[ 4^{3x} +4^{3x+2} = 4^{3x} (1+ 4^2 ) \]
\[ 4^{3x} +4^{3x+2} = 4^{3x} . 17 \]
\[ 4^{3x} +4^{3x+2} = 17 (4^{3x}) \]
Hence, the simplified result of a given exponential equation: $$ 4^{3x} +4^{3x+2} = \boldsymbol{17.4^3x} $$
All images/mathematical drawings were created with GeoGebra.
