JUMP TO TOPIC
Expression|Definition & Meaning
Definition
An expression is a mathematical sentence consisting of numbers, variables, and math operators. It should have at least one math operator and two terms, numbers, or variables to be called an expression.
A math operation is performed in an expression between different terms, resulting in another term or value. Figure 1 shows a primary expression.
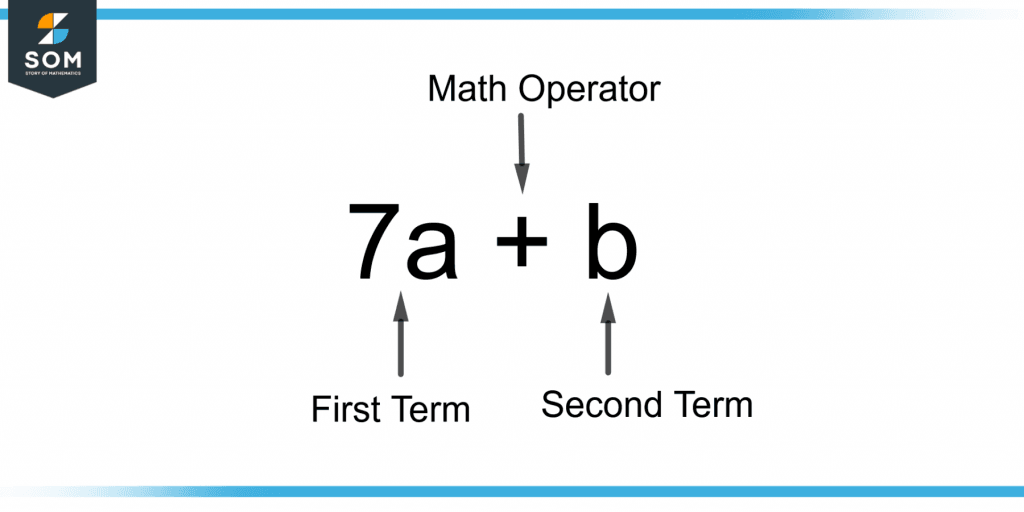
Figure 1 – Demonstration of an Expression
The addition operation is performed between two unlike terms 7a and b.
Components of an Expression
The following are required to make an expression in mathematics.
Numbers
Numbers are an important part of expressions. A math operation performed on two or more numbers is a basic expression. If a number is multiplied by a variable, it is known as the coefficient.
Variables
A variable is an unknown quantity in an expression. An alphabet or any symbol denotes it. Expression with variables is used in Algebra either to simplify them or to solve them for the unknown variables in equation form.
Terms
A term in mathematics is defined as a number, a variable, a number multiplied by a variable, many variables multiplied by each other, or variables multiplied by a number.
A variable should only be multiplied and not added or subtracted to form a term. For example, 5, x, 2z, abc, and 4lmn are different types of terms.
An expression can consist of a single term or multiple terms. There are two types of terms.
Like Terms
Like terms are the terms having the same variable with the same power. For example, 8b and 2b are like terms having the variable b with power 1.
These terms can be simplified in an expression by adding or subtracting.
Unlike Terms
The terms having different variables or the same variables with different powers are known as, unlike terms. For example, 4x and 2y are unlike terms. Similarly, 3c$\mathsf{^2}$ and 5c$\mathsf{^3}$ are also unlike terms.
An expression consisting of unlike terms cannot be simplified.
Math Operators
Math operators have a unique function applied to elements to produce a certain result. The basic operators are addition, subtraction, multiplication, and division.
Multiplication is a form of repeated additions and division is a form of repeated subtraction.
An expression cannot be formed without an operator. The terms on which the operation is applied are also known as the operands.
Figure 2 shows all the components of an expression.

Figure 2 – Components of an Expression
Types of Expressions
There are three types of expressions.
Numeric Expressions
An expression consisting of only numbers is known as a numeric expression. The math operation is done on numbers also known as constants.
For example, 9(2 + 5) is a numeric expression with addition and multiplication as its operators.
Fractional Expressions
These expressions have fractions as their terms. For example, 2/3 – 1/4 is a fractional expression.
Algebraic Expressions
Expressions consisting of variables, operators, and constants are known as algebraic expressions. For example, 7x + 6 – 5y is an algebraic expression with variables x and y.
Figure 3 shows the types of expressions.

Figure 3 – Types of Expressions
Types of Algebraic Expressions
Algebraic expressions have an essential role in Algebra. Depending on the number of terms, there are four main types of algebraic expressions.
Monomial Expression
A monomial expression consists of only one algebraic term. For example, 3x is a monomial expression.
Binomial Expression
“Bi” means two. So, a binomial expression consists of two terms only. For example, 3 + 2z is a one-variable binomial expression of variable z.
Trinomial Expression
A trinomial expression consists of three terms. For example, p + 3q + 6r is a trinomial expression of three variables p, q, and r.
Polynomial Expression
An expression consisting of more than three terms is known as a polynomial expression. The expression 2l + 5m + n – 7r + 6 is a polynomial with variables l, m, n, and r.
Figure 4 shows the four types of algebraic expressions.

Figure 4 – Types of Algebraic Expressions
Expressions in Equations
An equation is formed with expressions. It consists of an equality sign “=” and can have two expressions on both of its sides. Figure 5 shows an equation with an expression on its left-hand side.
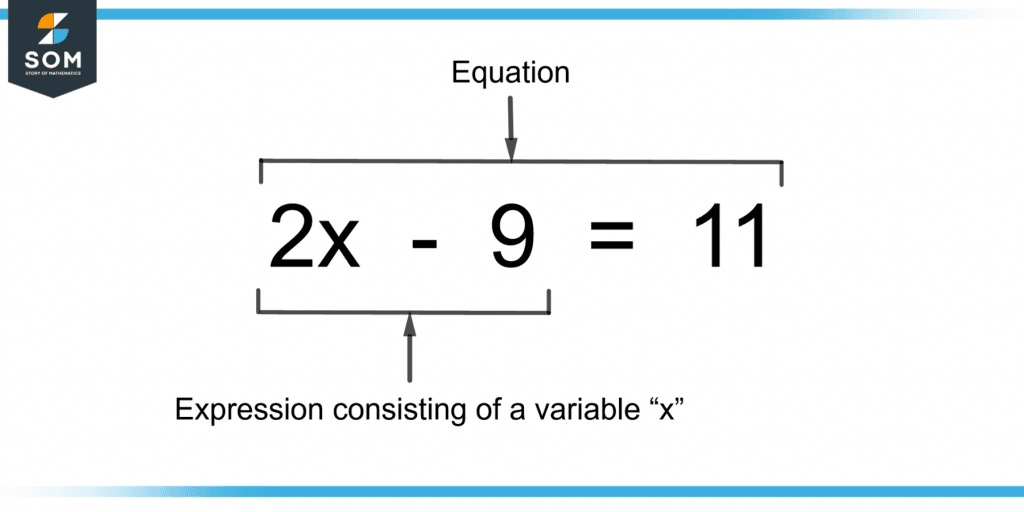
Figure 5 – Expression Within An Equation
The above equation can be solved by adding 9 on both sides which makes the right-hand side an expression too.
2x – 9 + 9 = 11 + 9
2x = 20
Dividing 2 into both sides gives the value of x:
x = 10
Hence, expressions are used in equations to solve for unknown variables.
Rules To Solve Expressions
The following acronyms are used to solve expressions.
PEMDAS
PEMDAS stands for “Parenthesis Exponent Multiplication Division Addition Subtraction”. This is the order of operations followed to solve the mathematical expressions.
The highest priority is of solving parentheses, then the terms with powers, and so on.
BIDMAS
Another acronym used is BIDMAS. It stands for “Brackets Index Division Multiplication Addition Subtraction”. It is the same as PEMDAS.
It is used for expressions consisting of more than one math operations.
Extracting Expressions From Sentences
Word problems contain sentences that need to be translated into mathematical expressions to solve. For example, the sum of 3 and 8 forms an expression as 3 + 8.
If 2 is subtracted from 4x, the expression will be 4x – 2. The product of 3 and 6x is expressed as 3(6x). 3 divided by 4 will be written as 3/4.
An Example of Evaluating Expressions
Solve the following algebraic expressions:
a) 5x + 8 – 2y + 3x – 6y – 2
b) 2(3l + 5m) – 3(l + 4m)
Solution
a) 5x + 8 – 2y + 3x – 6y – 2
At first, the like terms should be placed together as:
5x + 3x – 2y – 6y + 8 – 2
Solving the like terms gives:
8x – 8y + 6
The final expression is 8x – 8y + 6.
b) 2(3l + 5m) – 3(l + 4m)
By the distributive law, solving the parentheses gives:
6l + 10m – 3l – 12m
Solving the like terms gives:
6l – 3l + 10m – 12m
3l – 2m
So, the simplified expression is 3l – 2m.
All the images are created using GeoGebra.
