Extrema|Definition & Meaning

The point at which the function’s maximum or minimum value is attained is known as the absolute extremum (or global extremum) of the function in the given interval. The absolute extremum, or the point where the value of the entire function is at its highest or lowest is frequently the interval given, which is the domain of the function. 

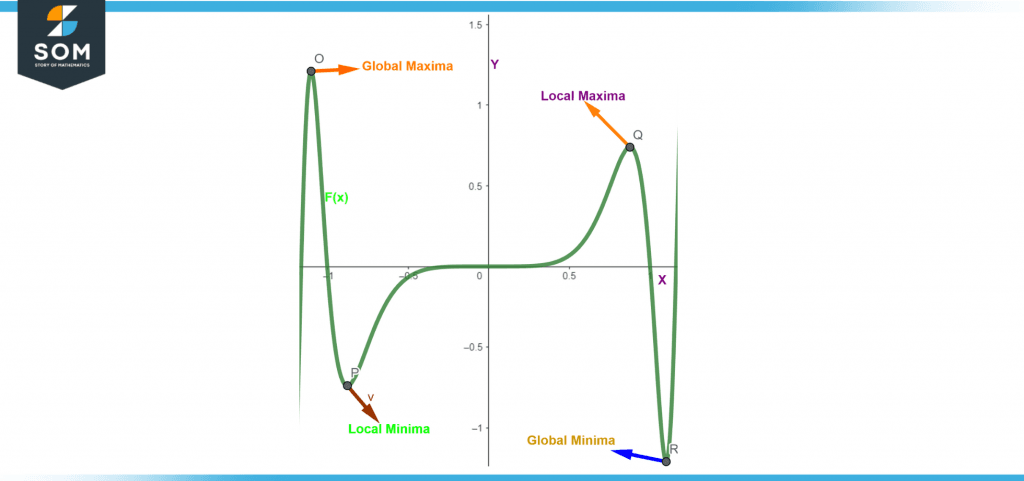
Figure 1 – Extrema points labelled at points O, V, Q, and R

Extrema (maximum and minimum values) are significant because they reveal a lot about a function and help with optimality-related questions. Numerous tools in calculus can be used to quickly identify the location and type of extrema.

Local Minima and Maxima

Local maxima and minima are maxima and minima of the function that occur within a given interval. The value of a function at a location in an interval where the values of the function are the highest is known as a local maxima nearby are consistently lower than the value of the function at that point.

Local Maxima: If a point x = u is in the neighborhood of b, i.e. in (u-Δ, u+Δ) where Δ can be adjusted to arbitrarily small, f(x) < f(u) for all x (u-Δ, u+Δ)\{u}, then that point is a local maximum for f(x). In  Simple terms, this means that f(u) should be the maximum in the small region (interval) around x = u.

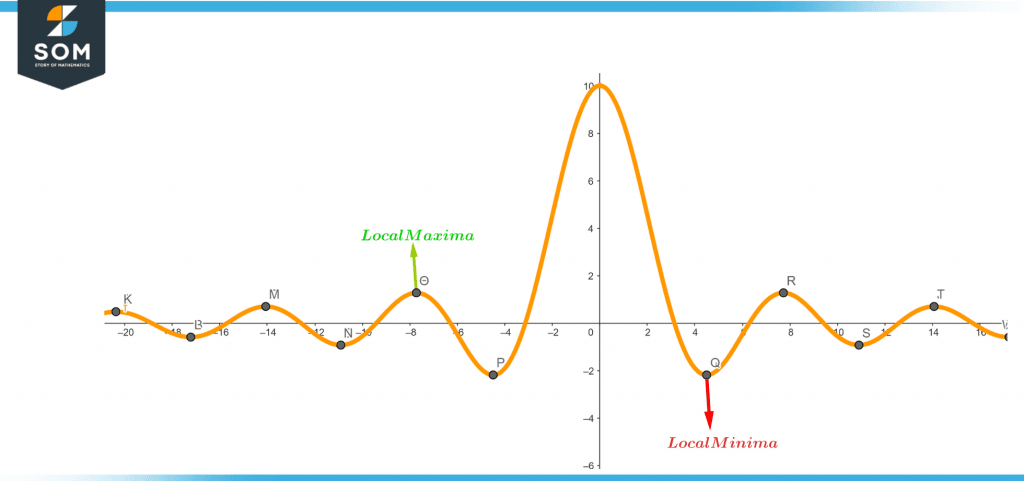
Figure 2 – Local Maxima at point O and Local Minima at point Q

Local Minimum: If a point x = k is in the neighborhood of f(x), i.e. in ( k-𝛿, k+𝛿 ), (where 𝛿 can have arbitrarily small values), and f(x) > f(k) for all x ( k-𝛿,k+𝛿 ) \ {k}, then the point is a local minimum for f(x). This means that f(k) should be the minimum in the small interval that surrounds x = k.

Global (Absolute) Maxima and Minima

Global maxima of a function refers to its highest point within its entire domain, whereas the Global minima of a function refers to its lowest point within its entire domain. Over the entire domain, a function can only have one Global maximum and one Global minimum. The Absolute maxima and Absolute minima of the function are another name for the global maxima and minima of the function.

Global maximums: If f(b) ≥f(x) where x is an element of D  (f(x) domain), then a point x = s is a point of global maximum for f(x).
Global minimum:  If f(s) ≤ f(x) where x is an element of D  (f(x) domain), then a point x = s  is a point of global minimum for f(x).
The function’s global maxima and minima are shown in the image below at x = m and n, respectively.

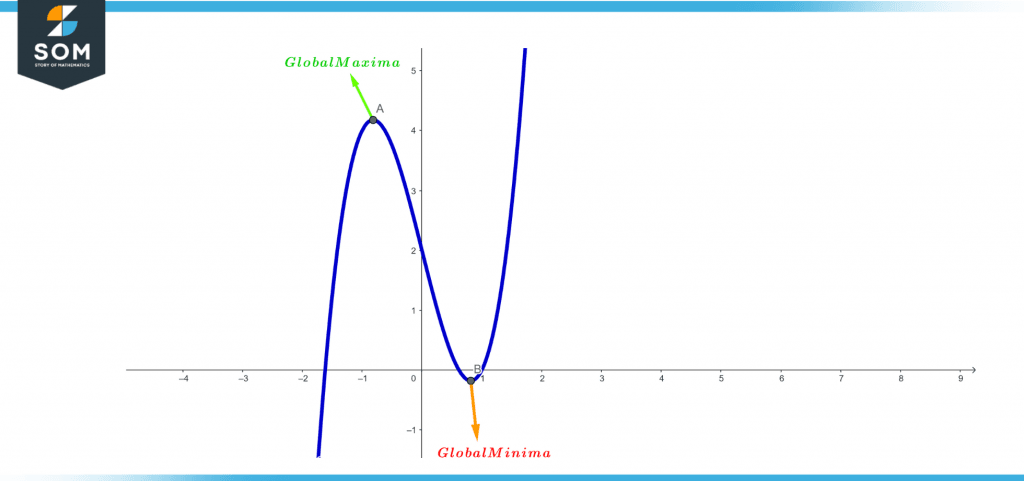
Figure 3 – Global Maxima at point A and Global Minima at point B

How Can We Find a Function’s Maxima and Minima?

Both the first-order derivative test and the second-order derivative test can be used to determine a function’s maximum and minimum. The quickest methods for locating a function’s maxima and minima are derivative tests. Let’s go over each one individually.

Maxima and Minima First-order Derivative Test

A function’s first derivative contains the slope.The slope of the curve rises as we approach the maximum point.. As we get farther away from the maximum point, the slope of the curve decreases. Similar to this, the slope of the function decreases as we get closer to the minimum point, at the minimum point it reaches 0, and then start increasing as we get farther away from the minimum point. We can determine the point’s maxima or minima using this data.

Let’s say we have a function f defined in an open interval I, which is continuous at the critical point, and f'(c) = 0. (slope is 0 at c). Once we have determined the nature of f'(x) and its values at the curve’s left and rightmost points, we can predict what the given point will be.

Local maxima: The maximum value of the function in that range is given by f(c) if f'(x) shifts from positive to negative as x increases through point c.
Local minima: The minimum value of the function in that range is given by f(c) if, at point c, f'(x) changes from a negative to a positive sign as x increases.

Point of inflection: Point c is referred to as the point of inflection if the sign of f'(x) does not change as x increases via c and point c is neither the maximum nor minimum of the function.

Maxima and Minima Second-order Derivative Test

If the slope at the critical point x = b (f'(b) = 0), the second-order derivative test for maxima and minima determines the function of first derivative. in which case the second derivative of the function is determined. if the function’s second derivative falls inside the specified range. The given point will be:

Local maxima: If f”(b) is less than 0.
Local minima: f”(b) is greater than 0.
The test is invalid if f”(b) is 0.

Important Information About Minima and Maxima

• The curve of a function has peaks and valleys called maxima and minima.
• There can only be one global maximum and one global minimum for a function throughout the entire domain.
• If f is either rising or falling with respect to I, f is said to be a monotonous function in the interval I.

An Example of Solving for Maxima and Minima

Locate a function’s maximum and minimum points.

y = 10x$\mathsf{^3}$ + 10x$\mathsf{^2}$ + 1

Solution

Given function:

y = 10x$\mathsf{^3}$ + 10x$\mathsf{^2}$ + 1

Using a second-order derivative test to determine a function’s maximum and minimum. Taking first order derivative of:

y = 10x$\mathsf{^3}$ + 10x$\mathsf{^2}$ + 1 — (equation 1)

Differentiate both sides of equation 1 with relation to x:

\[ \mathsf{\frac{dy}{dx} =  \frac{d}{dx}(10x^3)-\frac{d}{dx}(10x^2)+\frac{d}{dx}(1)} \]

$\Rightarrow \mathsf{\dfrac{dy}{dx}}$ = 30x$\mathsf{^2}$ + 20x  — (equation 2)

For finding the critical points, put $\mathsf{ \dfrac{dy}{dx}} = 0$:

⇒ 30x$\mathsf{^2}$ + 20x = 0

⇒ 10x ( 3x +2 ) = 0

⇒ x = 0, -2/3

The critical points are 0 & -2/3.

Differentiate both sides of equation 2 with relation to x:

\[ ⇒ \mathsf{\frac{d^2y}{dx^2} = \frac{d}{dx}(30x^2) + \frac{d}{dx}(20x)} \]

= 60x +20

Put the values of x now, and determine the maximum or minimum value.

At x = 0:

$\mathsf{\dfrac{d^2y}{dx^2}}$ = 60(0) + 20 = 20 > 0

hence x = 0 is a point of minima. At x = -2/3:

$\mathsf{\dfrac{d^2y}{dx^2}}$ = 60(-2/3) + 20 = -20 < 0

hence x = -2/3 is a point of maxima.

In conclusion,  at x = -2/3, the function is maximum, while at x = 0, it is at its minimum.

All images/mathematical drawings were created with GeoGebra.

Extrapolation Definition < Glossary Index > Face Definition