Face|Definition & Meaning

To understand the concept of faces we need to understand some related terms as well. These terms include vertices and edges. In the subsequent sections, all three of these terms are explained with the help of suitable examples and diagrams. 

The following figure shows an example of a cube which serves as a preliminary introduction to these key concepts of geometry when we talk about the three dimensional and two dimensional shapes.

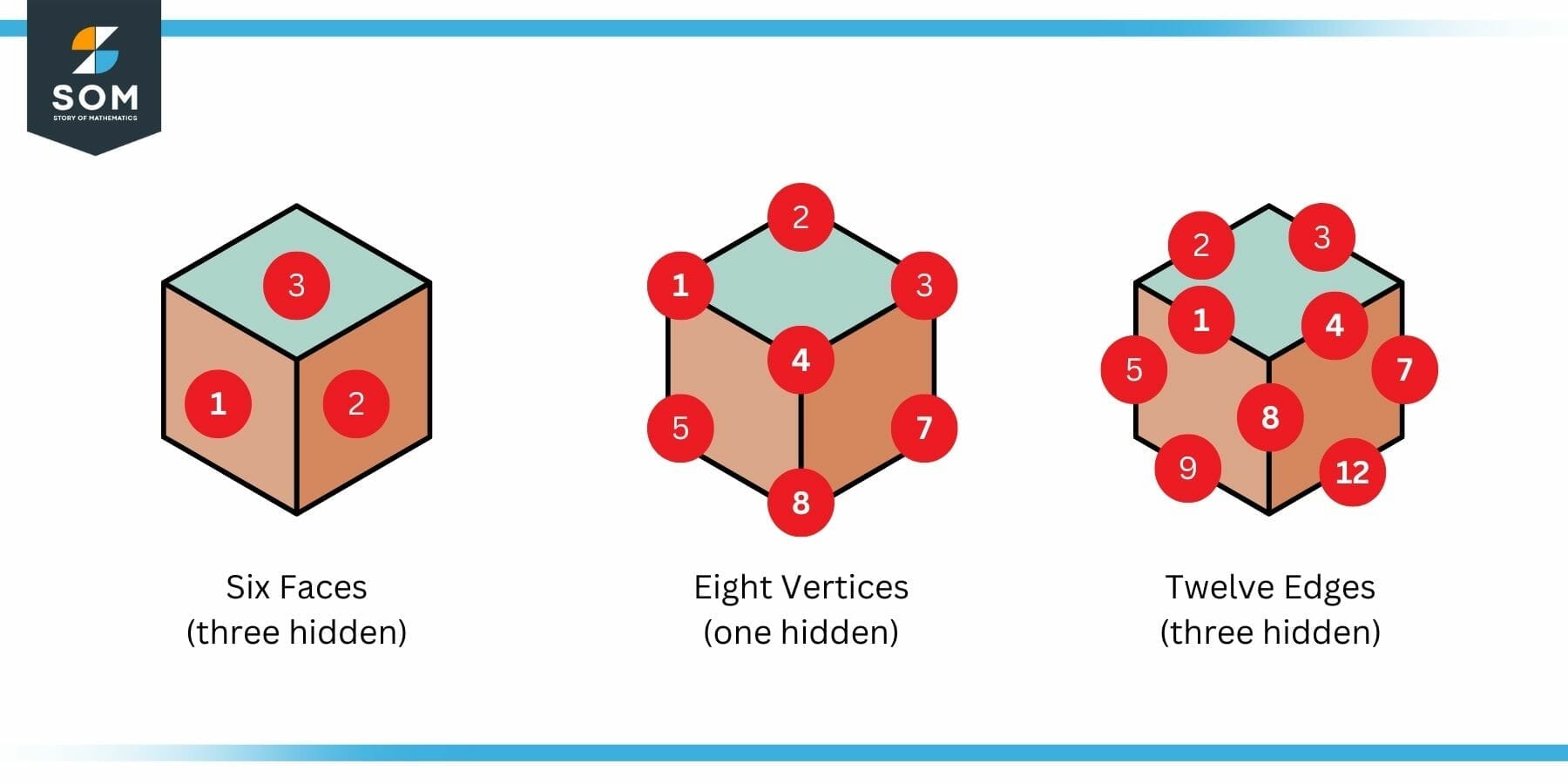
Figure 1: Faces, Edges and Vertices of a Cube

In this example, the cube has eight vertices, twelve edges, and six faces. The calculations become clearer as we introduce these concepts with the help of examples.

What Is a Face?

A face in geometry is a three-dimensional geometric shape’s planar (flat) surface. In short, the flat surface of a solid body is known as its face. It’s also important to realise that managing two-dimensional forms is physically impossible because everything around us has three dimensions.

Consider the cube given in the figure 1. The smooth surface that makes up this cube’s front is known as its face. A cube has six faces, however, only three are visible in the above figure no. 1.

Several faces may be seen on many solid shapes. For instance, a cuboid has six faces as shown in the figure below.

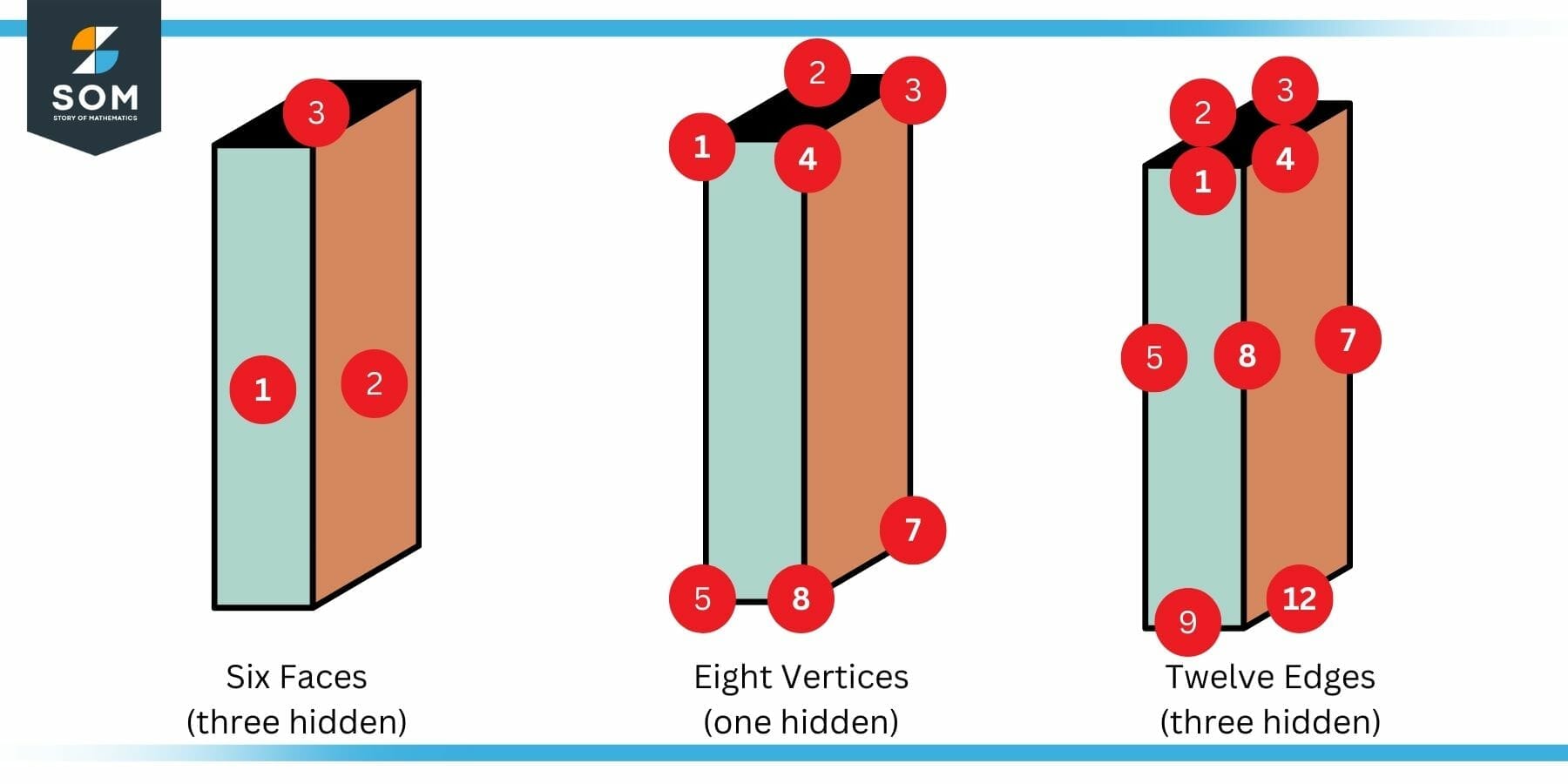
Figure 2: Faces, Edges and Vertices of a Cuboid

Some geometrical shapes or diagrams are faceless. For instance, a pyramid has faces but a sphere has no face. So a face is made up of one flat surface. In fact, a face is any flat area. The pictures 3 and 4 given below show the faces of a cone and a prism.

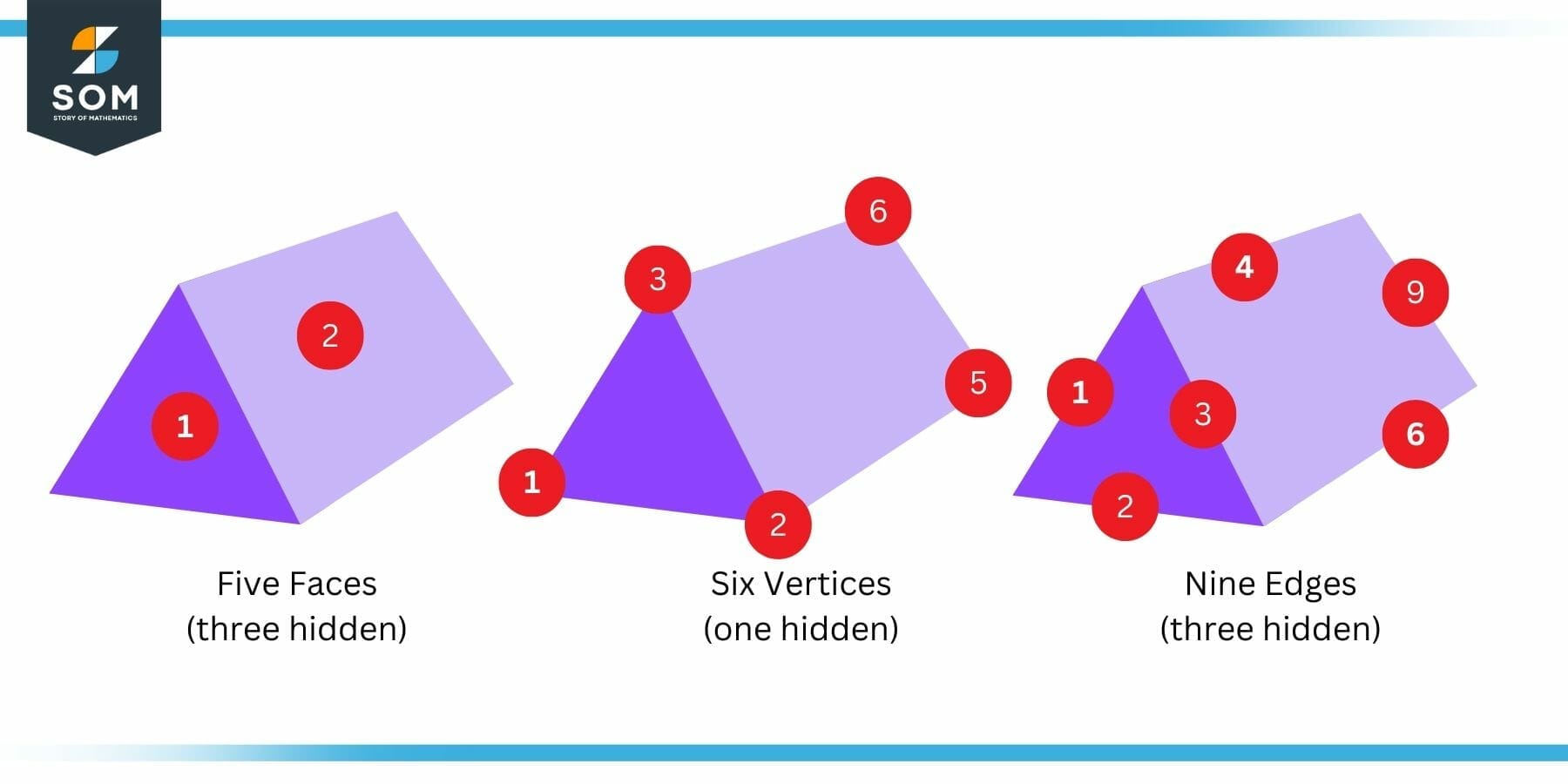
Figure 3: Faces, Edges and Vertices of a Prism

The term “face” refers to any of an object’s distinctive flat surfaces. There are four faces on this tetrahedron as shown in figure 5. Because it could be the face of a polyhedron or the edge of a polygon, the word “side” is not very precise. A solid’s face is any one flat surface. Solids can have several faces. A face is a flat surface (a planar region) that forms part of a solid object’s border.

What Is a Vertex?

In any three-dimensional or two dimensional shape, vertices are the locations where two or more line segments or edges cross. They can be thought of like a corner. A single such corner is called a vertex and multiple such corners are termed as vertices.

For instance, the cube shown in the figure no. 1 has eight vertices. One of the vertices is hidden in this figure and only seven are displayed. The cone shape shown in the figure below, however, only has one vertex.

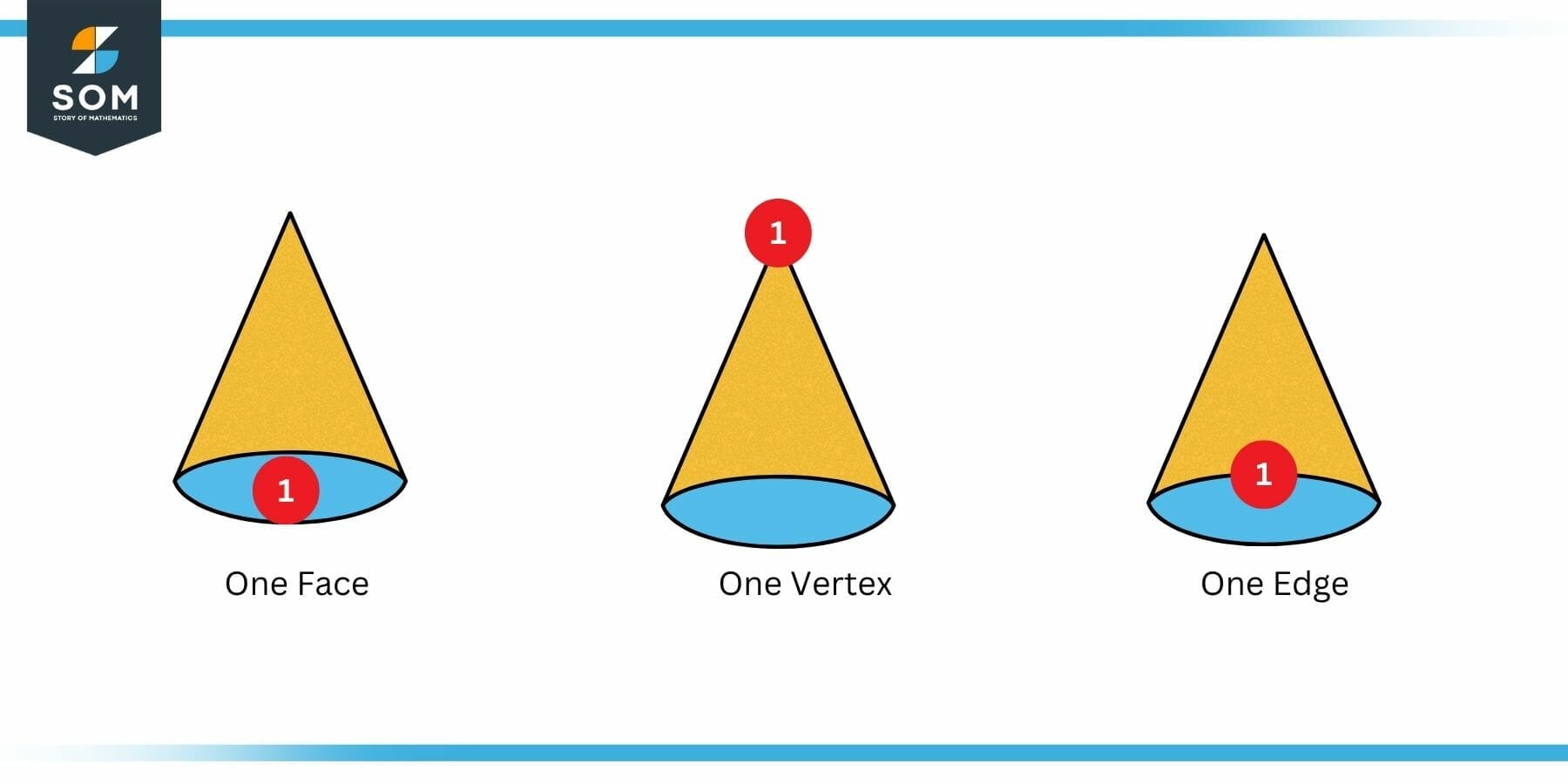
Figure 4: Faces, Edges and Vertices of a Cone

In short, vertex is another name for a corner. Many solids have many vertices or a large number of vertices.

What Are Edges?

The line segments known as edges act as the meeting places for the faces of a shape and join one vertex to the next. They may be used to describe both two dimensional and three dimensional geometrical shapes. Some shapes, like hemispheres, have curved edges even though many forms have straight edges and lines.

A cube, shown in the figure 1, has twelve straight line edges. Nine out of these twelve are visible in the diagram while three are hidden. A quick glance reveals that this cube’s faces intersect one another in a straight line.

So we can say that a segment of a line joining two faces or connecting two vertices (corner points) on a polygon’s boundary is referred to as an edge.  Many solid forms have several edges. As another example, the tetrahedron shown in the following figure has six edges.

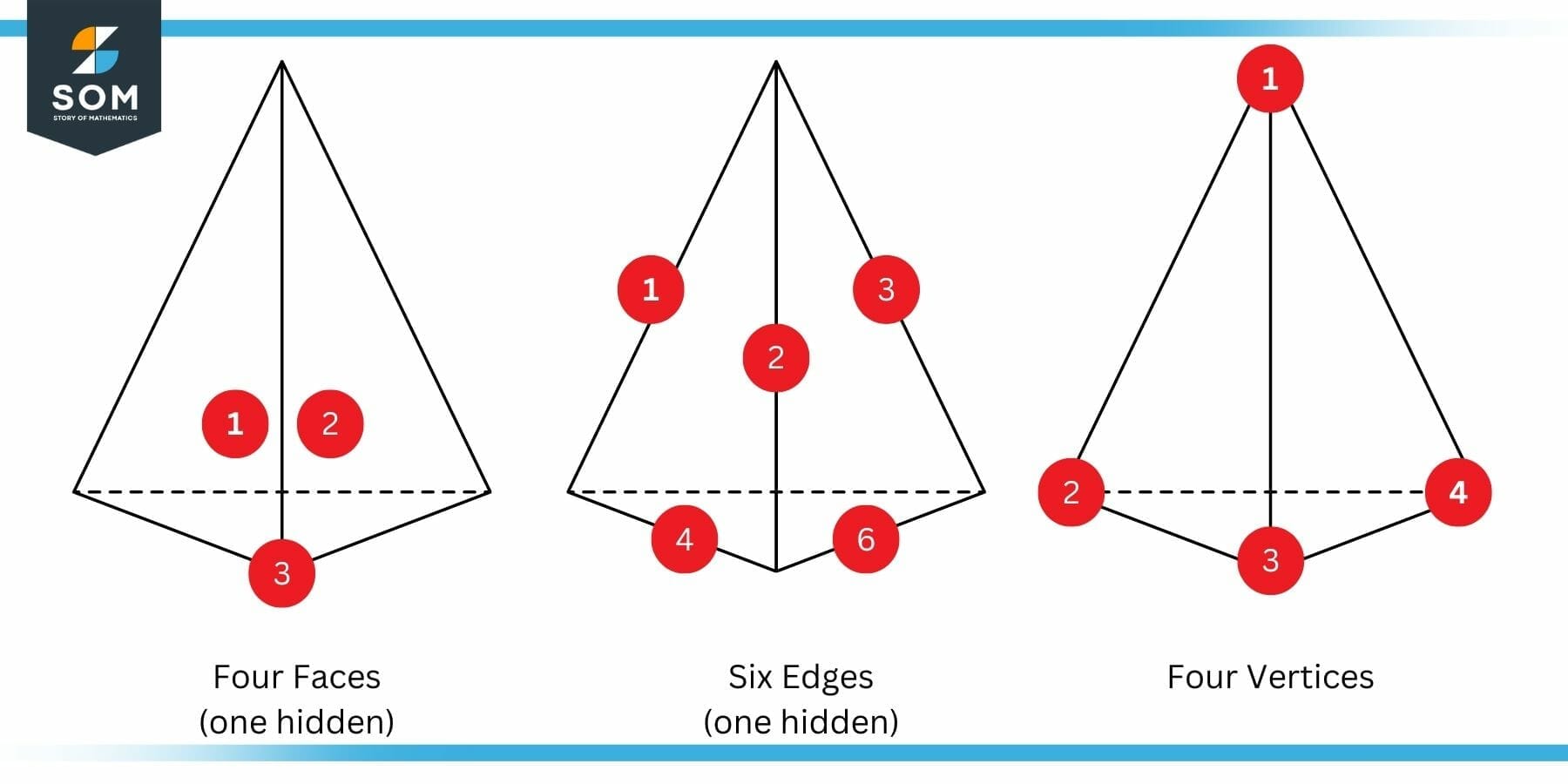
Figure 5: Faces, Edges and Vertices of a Tetrahedron

Euler’s Theorem

The Euler theorem, named after Leonhard Euler, is one of the most important mathematical theorems. The link between a polyhedron’s face, vertex, and edge counts is established by the theorem. To understand Euler’s theorem, we first need to understand the term Polyhedron. Euler’s polyhedron formula is accurate for the majority of polyhedron types.

What Is a Polyhedron?

A closed-space object formed entirely of polygons is called a polyhedron. The English term “polyhedron” is derived from the Greek words “poly” and “hedron,” which combined denote a base or seat.

In other words, a closed solid shape with flat sides and straight edges is known as a polyhedron. There are several varieties of polyhedra. Due of its rounded edges, a cylinder is not a polyhedron; in contrast, a cube is an illustration of one.

Polyhedrons have faces, edges, and vertices. The edges of a polyhedron are made up of line segments that span two faces. Vertices are the intersections of three or more edges. In summary, a polyhedron is a three-dimensional solid with faces acting as its only boundary.

Mathematical Form of Euler’s Theorem

Euler’s Theorem shows how a polyhedron’s faces, vertices, and edges are connected. According to this theorem, for many solid shapes, the total of the number of faces plus the number of vertices minus the number of edges is always equal to two.

Mathematically:

( Faces ) + ( Vertices ) – ( Edges ) = 2

Let’s test this condition for our initial example of the cube. We already know that a cube has twelve edges, eight vertices, and six faces. So putting these values in the above formula:

( 6 ) + ( 8 ) – ( 12 ) = 14 – 12 = 2

Hence, the Euler’s theorem holds true for the case of cube. Its important to reiterate that Euler’s Formula only holds true for the Polyhedrons.

Numerical Example of Faces

Given the following geometrical shape (Octahedron), find the number of faces, edges and vertices. Also check if the Euler’s theorem holds true for this shape or not?

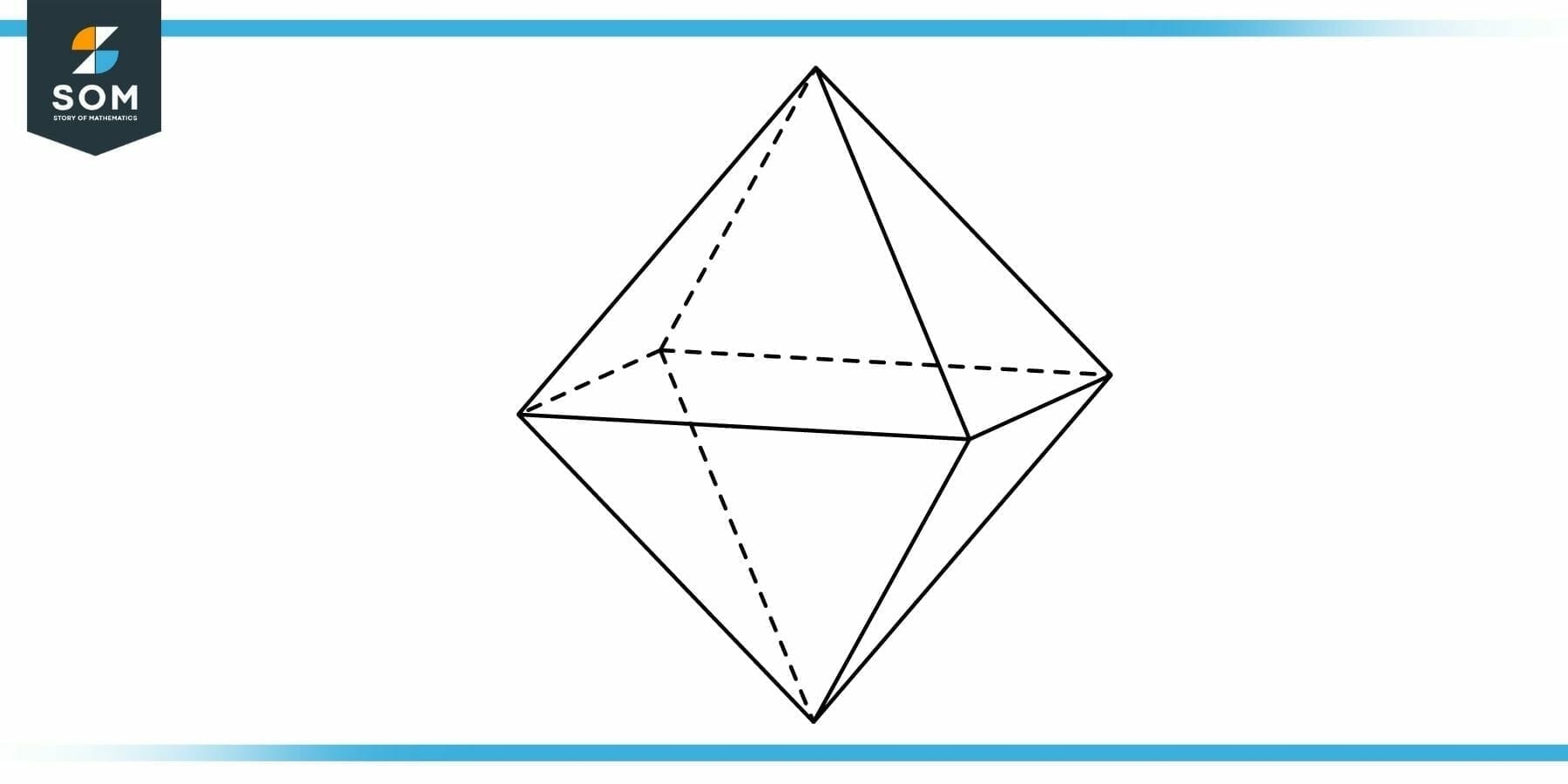
Figure 6: Numerical Example for Faces, Edges and Vertices (Octahedron)

Solution

The given figure has eight faces, twelve edges and six vertices.

Putting these values in the Euler’s formula:

( 8 ) + ( 6 ) – ( 12 ) = 14 – 12 = 2

Hence, the Euler’s theorem holds true for the case of cube.

All figures and charts have been constructed using GeoGebra.

Extrema Definition < Glossary Index > Factor Definition