Factor|Definition & Meaning

What Is a Factor? 

Factors are a basic concept in mathematics that refer to the whole numbers that exactly divide another number. Let’s say we have the number 12, and the maximum possible factors of 12 can be 1, 2, 3, 4, 6, and the number 12 itself, as these numbers can be multiplied together to equal 12.

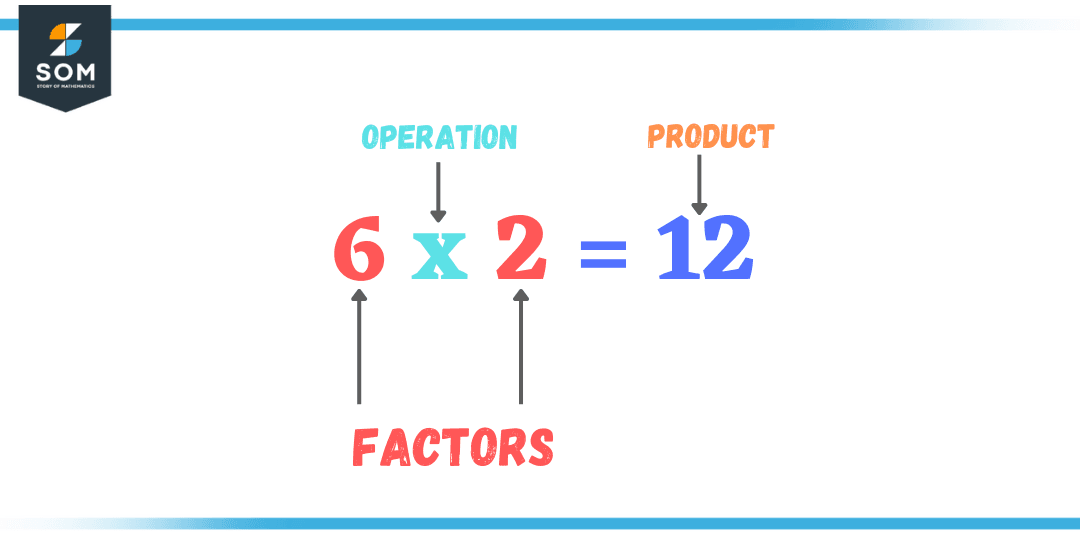
Figure 1 – Factors are the numbers that make up the product

There are some related ideas to factors, including prime numbers, greatest common factors (GCF), and least common multiples (LCM).

Prime numbers are unique numbers that can only be divisible by two numerals, i.e., 1 and the numbers themselves, while GCF represents the largest number that exactly divides two or more numbers. LCM, on the other hand, can be seen as the most diminutive number, which is only divisible by two or more than two numbers.

Factors have a significant impact in various areas of mathematics, including arithmetic, algebra, and geometry. In arithmetic, factors are utilized to determine the greatest common divisor (GCD) and LCM of two or more numbers. In algebra, they help simplify expressions and solve equations, while in geometry, they’re used to calculate areas and volumes of shapes.

Factors also play a crucial role in number theory, where researchers study the properties and patterns of numbers. For example, the distribution of prime numbers and the relationship between prime and composite numbers are studied in number theory.

Finding the factors of a number can be done by listing all the numbers that divide the original number evenly or by dividing the number by each whole number until there’s no longer a remainder.

If we multiply two numbers and it produces a whole number as a product, then the numbers being multiplied are known as factors. In other words, factors are also known as divisors as they entirely divide the numbers and yield zero remainders.

Factors provide whole numbers as answers, but they can be positive as well as negative. For example, factors of 20 are 1, 2, 4, 5, and 10 because these numbers factor 20 but -1, -2, -4, -5, and -10 are also factors of 20 as two negative numbers when multiplied, providing a positive number. But generally, only positive factors are considered. 

Properties of Factors

The following are some properties of factors:

• Every number has one factor in common, i.e., 1.
• Natural numbers are their own factors.
• More than two factors exist for each composite number. 
• Factors can only be whole numbers or integers; they can never be decimals or fractions.
• 1 and the number itself are the only factors of prime numbers. 
• Except for 0 and 1, every whole number has, at the minimum, two factors.
• All the even numbers have one typical factor, i.e., 2.
• Factors are always lesser than or equal to the assigned number.
• The number of factors can never be infinite; it is always finite.
• Factors can be estimated by operating division and multiplication.

Factors and Multiples

Since factors are the numbers being multiplied, multiples are the answers to these multiplications. In other words, multiples are the product of any two factors. Let us clear this concept using an example; we know that 2*3=6. Here, 2 and 3 are the factors of 6, and 6 is a multiple of 2 and 3. Moreover, multiples of 6 are 6,12,18,24,30,36, and so on.

Multiples can be noticed in multiplication tables. Unlike factors, Multiples are the exceeding values or equal values to the assigned number. 

Figure 2 – Factors and multiples of a particular number

How To Find Factors?

Now we must learn the methods of obtaining factors. One can easily and quickly estimate the factors if one has a good command over multiplication tables. The simplest methods of finding factors are multiplication and division. Let us discuss how to find factors using these two methods:

Finding Factors Using Multiplication

We can estimate the factors by operating multiplication. First, we have to list down all the numbers that multiply to give the assigned number, for instance, 12. Now start making pairs of the two numbers like 1*12, 2*6, and 3*4. From 1 to 9, only these numbers multiply to give 12, so both of these multiplicands, i.e., 1,2,3,4,6 and 12, are the factors of 12.

Finding Factors Using Division

Finding a single factor or multiple factors of a number is an easy method when using division. To estimate the factors using the division method, we have to list all the numbers that wholly divide the assigned number, let’s suppose the assigned number is 16. From 1 to 9, the numbers that give zero remainders are 16\1,16\2, 16\4, 16\8, and 16\16. So 1,2,4,8, and 16 are the factors of 16. 

Factor Tree

It is a method to express and find the factors of any number. The numbers that multiply to give a particular number can be written in a tree-like shape. It is an easy and simple representation of factors.

The tree stops where the branches reach the prime numbers, and the factors are obtained. It is to be noted that 1 will not occur in the factor tree since it is not a prime number. Factor trees basically portray the prime factorization of numbers. Following is an example of a factor tree representation of 24.

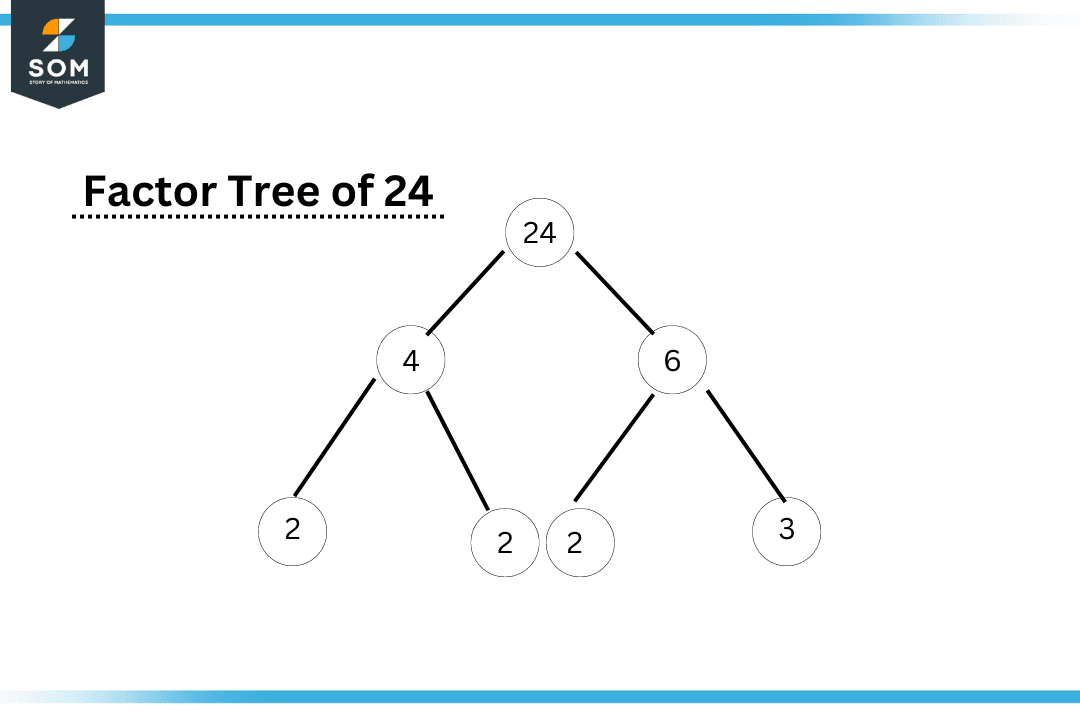
Figure 3 – A factor tree of the number 24

So, we get 2*2*2*3 as the prime factor of the number 24. Or it can also be written as (2$^3$)*3.

Types of Factors 

Factors can be categorized as common factors, prime factors, and the highest common factors. Let us discuss these types of factors in detail.

Common Factors 

If two or more numbers share some similar factors, then we can call these factors common factors. For example, common factors of 24 and 36 are 1,2,3,4,6 and 12 because both 24 and 36 are entirely divided by these numbers. The common divisor is another name for common factors.

Prime Factors 

The prime numbers that multiply in order to produce an integer are going by the name of prime factors. The method of evaluating prime factors is called prime factorization. For example, the prime factorization of 12 gives 2*2*3, so 2 and 3 are the prime factors of 12.

Highest Common Factor

As the name indicates, the highest common factor is the largest value among all the common factors of assigned numerals. To find the highest common factor, first, we have to find all the common factors of the two or more numbers. We discussed the common factors of 24 and 36. Here, 12 is the largest value among all the common factors, so it is the HCF of 24 and 36. HCF of 8 and 12 is shown in the figure below,

Figure 4 – The highest common factor of numbers 8 and 12 is computed as 4

Factors of Perfect Numbers

A number whose factors, when added, produce a number equivalent to itself is represented as the perfect number. The perfect number includes the sum of all the factors except the number itself. For example, 1, 2, and 3 are factors of 6. 1+2+3 = 6, so 6 is a perfect number.

Suppose another number, i.e., 10, factors of 10 are 1,2 and 5. 1+2+5 = 8; hence 10 is not a perfect number. The perfect number after 6 is 28. Every other number between 6 and 28 is not perfect. The number 28 has factors excluding itself, 1, 2, 4, 7, and 14. Adding them up, we get 28 as a result. Hence proved that 28 is a perfect number.

Factors of Algebraic Expression 

As natural numbers have factors, algebraic expressions can also be expressed in the form of factors. Starting with a simple example, let 12x be an algebraic expression. The factors of 12x are 1, 2, 3, 4, 6, 12, x, and 12x.

Now talking about a complex algebraic expression and finding its factors, we take 11x$^2$ + 12xy – 3z$^2$ as an algebraic expression. This expression comprises 3 terms, i.e., 11x$^2$, 12xy, and -3z$^2$. The factors of these individual terms are:

11x$^2$ = 1.11.x.x

12xy = 1.2.2.3.x.y

-3z$^2$ = -1.3.z.z

Factors of algebraic expressions can also be determined by using common factors, using identities, and by regrouping the terms.

By Using Common Factors

Determining the factors of algebraic expression by common factors, we understand this concept using an example as follows:

= 12xy$^2$ – 18yz$^2$

= 2.2.3.x.y.y – 2.3.3.y.z.z

= 2.3.y(2.x.y – 3.z.z)

= 6y(2xy – 3z$^2$)

By Using Regrouping Method

There are some expressions that do not have any factors in common, so we have to use a different method for finding factors. We name it a regrouping method.

Let us suppose an expression 16x + y – xy – 16. There is no common factor among these four terms, but the first and last terms have a common value; similarly, the middle two terms share a common value. Hence we can group these terms using the following steps:

= 16x – 16 – xy +y

= 16(x-1)-y(x-1)

= (16-y)(x-1)

So we can factorize an algebraic expression by regrouping its terms. 

By Using Identities  

In mathematics, there are some well-known identities or formulas which are used for finding the factors. These are as follows:

(a+b)$^2$ = a$^2$+2ab+b$^2$

(a-b)$^2$ = a$^2$-2ab+b$^2$

a$^2$-b$^2$ = (a+b)(a-b)

Let us take an algebraic expression, 16x$^2$ – 24xy + 9y$^2$. Factoring it using the identity as follows:

16x$^2$ – 24xy + 9y$^2$

=(4x)$^2$ – 2(4x)(3y) + (3y)$^2$

=(4x – 3y)$^2$

Hence, (4x – 3y)$^2$ is the factor of the expression 16x$^2$ – 24xy + 9y$^2$.

Factor Pairs 

When two integers multiply to give a certain numeral value, the combination of those integers is called factor pairs. In other words, it is a pair of two values that multiply to produce a product. There can be many factor pairs for a particular number except prime numbers. Since prime numbers have only 2 factors, so there can be only a 1-factor pair for them.

For example, factors of 7 are 1 and 7, so the factor pair for 7 is (1, 7). Multiplication tables make it easy to form factor pairs. For example, 2 and 12 are factors of 24, but they are not the only factors. 4 and 8 are also factors of 24. We can write it as (2, 12) and (4, 8) are the factors of 24.

Factor pairs can also be created for negative integers. Like (-2, -12) and (-4, -12) are also the factors of 24. Moreover, the factor pairs of decimals, fractions, and algebraic expressions can also be formed in a similar manner.

Expanding and Factoring

Expanding is the opposite of factoring. Since factoring splits a number or an equation into factors,  expanding multiplies factored values and returns back to the actual statement. Let us clarify this concept using an example.

Let 9y$^2$+24yz+16z$^2$ be an algebraic expression. Factors of this expression will be (3y+4z)$^2$ by using identities. (3y+4z)$^2$ is equal to (3y+4z)(3y+4z). Now if we want to expand it, we multiply both factors such that:

3y(3y+4z) + 4z(3y+4z) = 9y$^2$ + 12yz + 12yz + 16z$^2$ = 9y$^2$ + 24yz +16z$^2$

Thus, we proved that expanding and factoring are inverse of each other.

Daily Life Factoring

In daily life practices, we often utilize factors without realizing them. Factors are important for various daily grinds like if you want to group or divide something, calculate and exchange money, units converting and time distributing, distributing workload, calculating your traveling, factorization in coding, and many more.

So we can conclude that one can easily become efficient in dealing with these problems if one has a piece of great knowledge and command over factors and calculating them. 

Solved Examples Involving Factor Calculations

Example 1

Write down all the factors of 48 and 54. Also, find the highest common factor.

Solution 

Factors of 48 are:

1 * 48 = 48

2 * 24 = 48

3 * 16 = 48

4 * 12 = 48

6 * 8 = 48

Thus 48 has a total of 10 factors which are {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}.

Factors of 54 are:

1 * 54 = 54

2 * 27 = 54

3 * 18 = 54

6 * 9 = 54

Thus 54 has a total of 8 factors which are {1, 2, 3, 6, 9, 18, 27, 54}.

Common factors of 1, 2, 3, and 6. Out of these four factors, 6 is the highest common factor.

Example 2

Write all the positive and negative factor pairs of 105.

Solution 

Positive factor pairs of 105:

1 * 105 = 105   (1, 105)

3 * 35 = 105     (3, 35)

5 * 21 = 105     (5, 21)

7 * 15 = 105     (7, 15)

Negative factor pairs of 105:

-1 * -105 = 105   (-1, -105)

-3 * -35 = 105     (-3, -35)

-5 * -21 = 105     (-5, -21)

-7 * -15 = 105     (-7, -15)

All images are created using GeoGebra.

Face Definition < Glossary Index > Factor Tree Definition