Factor Tree|Definition & Meaning

How to Draw a Factor Tree? 

We may build a factor tree by factorizing a number until we achieve its prime factors. These variables are divided into sections and expressed like a tree. Let’s practice drawing the 200-factor tree as shown in figure 1 below:

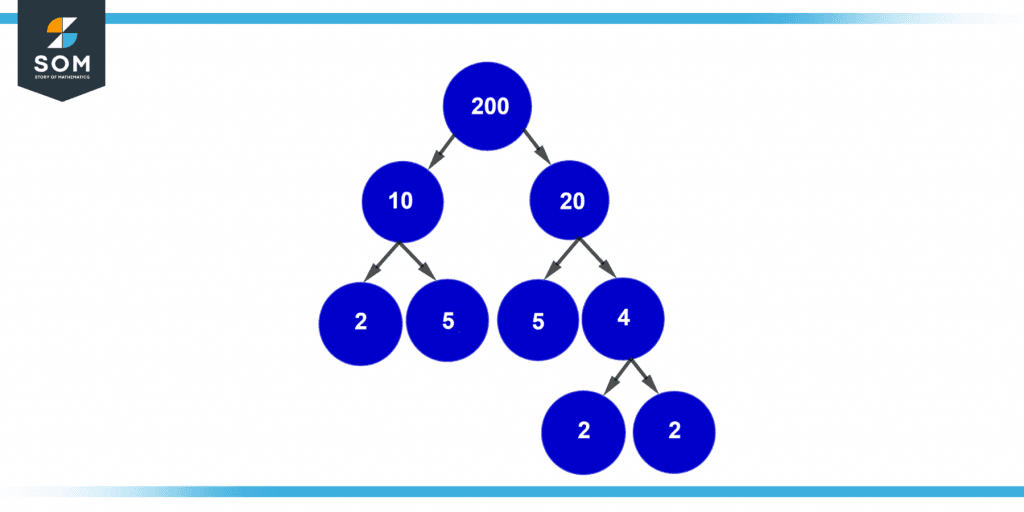
Figure 1 – Factor tree of 200

The factor tree approach may determine a number’s prime factors. Drawing the provided number’s branches and writing the elements at each branch’s conclusion accomplishes this.

The factor tree ends when we reach the number that cannot be divided further since all of its main attributes are recorded. All positive integers circled are now presented as the number’s prime factors. 

Let’s examine this by utilizing the factor tree approach to discover the factors of 200.

The procedures shown below can be used to compute the factors of 200. The 200-factor tree may be seen in the figure above.

Step 1: Find two factors of 200 as a first step. 10 and 20 are given.

Step 2: Check whether these components seem to be prime or not.

Step 3: Since 10 and 20 are both composite numbers, further factors can be added to them. Therefore, until we approach the prime numbers, we continue factorizing them and dividing them into branches.

Step 4: Two further divisions of 10—2 and 5—can be made here. Likewise, 20 may be divided into further 5 and 4. We now arrive at the prime integers 2 and 2. Since we know they can’t be further factorized, we circle them. The factor tree comes to an end here.

Step 5: The factors in square brackets are all listed as the prime factors for 200 in the last step. This demonstrates that 200’s prime factors are 2, 5, 5, 2, and 2.

Factors and Multiples

• Factors consist of the digits that split the given integer precisely. For a number to be claimed to be a component of any second number, it must be completely divided by the first quantity, leaving no residue. Simply put, the divisor is only a factor of a dividend if one number (the dividend) can be split precisely with any other number (the divisor). All numbers have two things in common: the number itself and the common component of one.
• Multiples are numbers that multiply one number by another to arrive at a specific number. A quantity is considered a multiple of a number if it is the outcome of that number and then another natural number. Multiples can be seen using a multiplication table.

Figure 2 below shows factors and multiples.

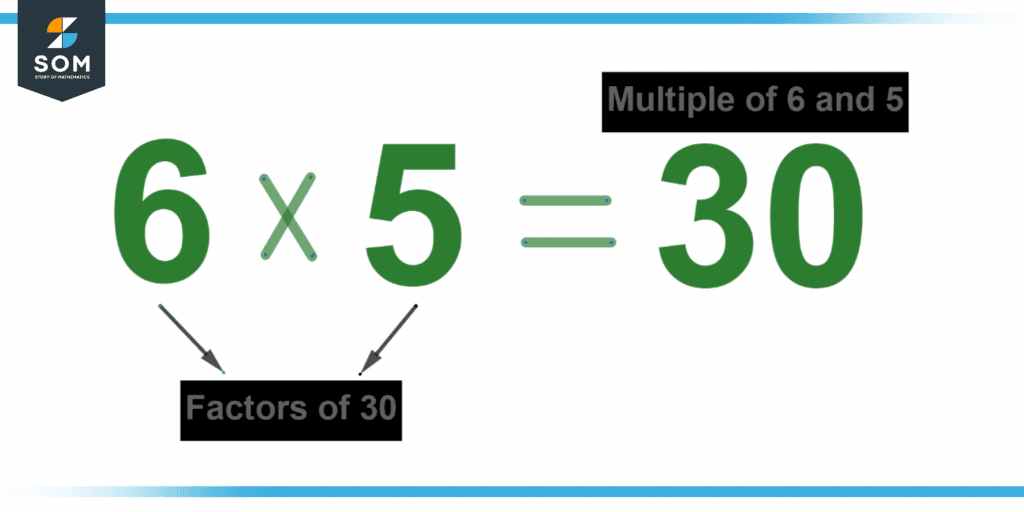
Figure 2 – Representation of factors and multiples.

Importance of Factor Trees

Factor trees are helpful for:

• Locate the lowest common multiple, often known as the least common multiple (LCM) or the high common factor (HCF).
• Determine other numerical characteristics, such as a number’s prime, square, or cube status.
• To avoid using decimals while working with diverse values, we can convert them to whole numbers.

Because we are dealing with positive factors, a factor tree doesn’t contain decimals (natural numbers).

Highest Common Factor

HCF is the greatest common divisor or gcd, and the most significant positive number divides two or more portions without producing a remainder.

Least Common Multiple

The least common multiple, In mathematics, the LCM of two numbers, like x and y, is denoted by the symbol LCM (x,y). The LCM is the most minor or smallest prime number divisible by x and y.

 Square, Cube, and Prime Numbers

• Any integer that has been multiplied by itself is a square.
• A cube number is an integer that multiplies by two to form a new number.
• Any natural integer higher than one that is not the sum of two extremely small natural numbers is considered a prime number. A composite number is a natural number more significant than another that is not prime.

Prime Factor Tree

By taking prime numbers into account, a prime factor tree is produced. The prime numbers spanning 1 and 20 must be retained in memory. The original number was split into two branches using two factors. We have produced a prime factor tree since each branch now has a prime number at the end.

If the values weren’t primes, we would continue factoring them until each branch culminated in a prime integer.

Figure 3 below shows the prime factor tree of 51.

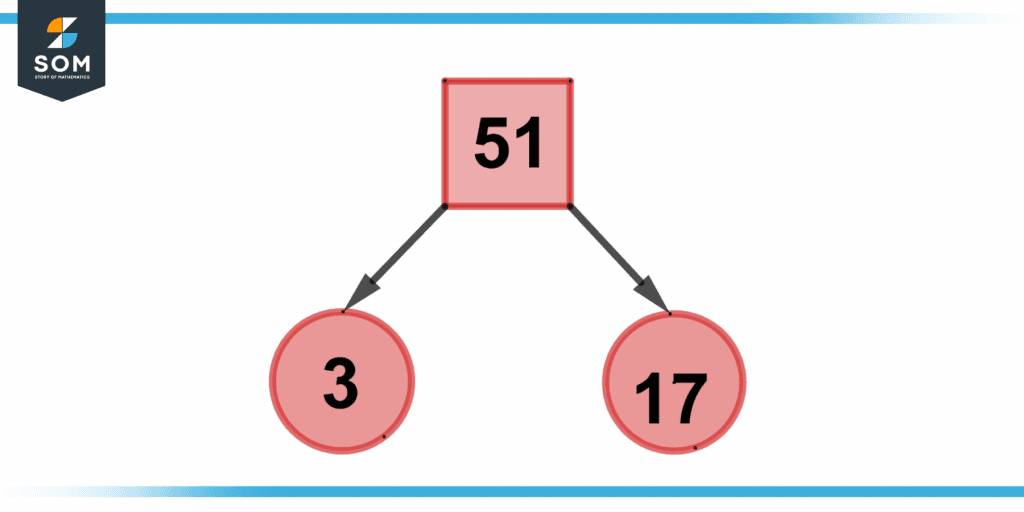
Figure 3 – Representation of prime number factor tree of 51.

A number’s factor tree is not unique, even though the prime factors were.

This indicates that various factor trees may yield the same result for prime factors of a given number.

How To Use a Factor Tree

1. Create two branches below the number and write the value at the top of a factor tree.
2. A factor combination of the number mentioned above should be used to fill in the branches.
3. Continually terminate each branch with a prime integer.
4. The answer should be written in a separate work line in index form.

Index Form

Standard index form is composing and calculating with massive and tiny numbers. When a number is written as the sum of its prime components, it should be in index form.

Example of Prime Trees

During his homework, a college student is given the following 100-factor tree. The student has to fill in the missing numbers in the tree. By using the techniques mentioned above, fill in the missing numbers.

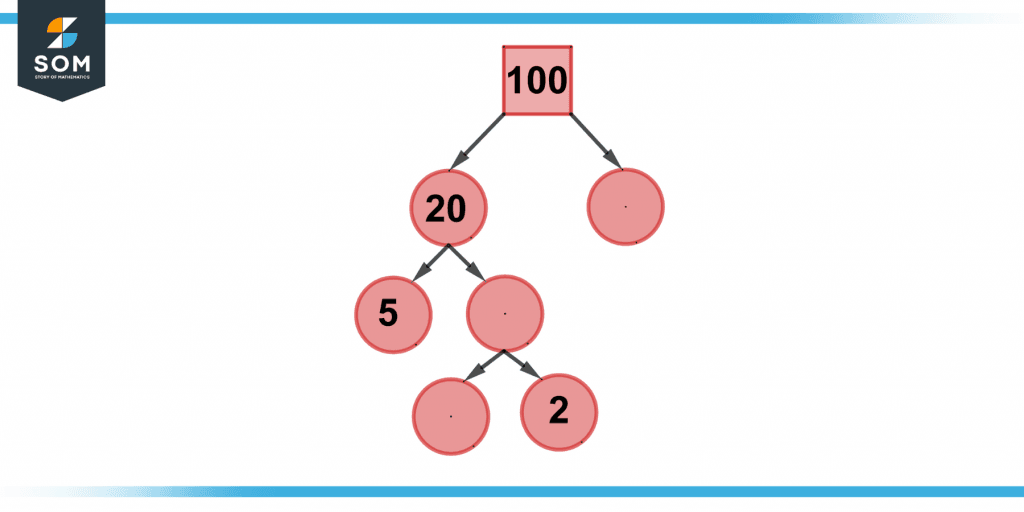
Figure 4 – Example of factor tree of 100 with missing numbers.

Solution

5 and 20 may be made out of 100. Then, as 5 is a prime number, it can be circled, and we further divide 20 into 5 and 4. Divide four into 2 and 2. Therefore,

a.) The first empty box’s number is 5.

b.) The value of the second empty circle is four.

c) The third and final missing box’s number is 2.

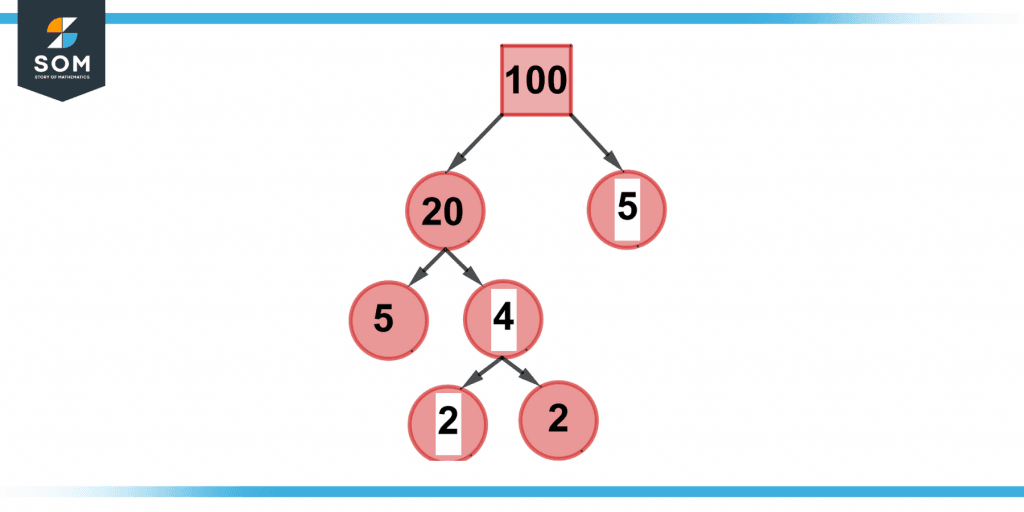
Figure 5 – Solved factor tree of 51.

All Images are made using GeoGebra.

Factor Definition < Glossary Index > Factoring Definition